A rectangle loop of size $l \times b$ carrying a steady current I is placed in a uniform magnetic field $\to B$ . Prove that the torque $\to τ$ acting on the loop is given by $\to τ = \to m \times \to B$ , where $\to m$ is the magnetic moment of the loop.

Text Solution

Verified by Experts

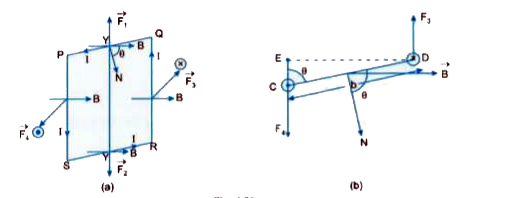
Consider a rectangular coil PQRS of length l and breadth b, carrying current I, placed in a uniform magnetic field B such that a vectro normal to the plane of the coil subtends an angle $θ$ from the direction of B.
In this situation forces $F_{1} and F_{2}$ having magnitude $I b B sin θ$ are acting on arms PQ and RS. The forces are equal, opposite nad collinear, hence they cancel out.
Again forces $F_{3} and F_{4}$ having magnitude $I l B$ are acting on each of the two arms QR and SP. These forces too are equal and opposite but these are non-collinear and form a couple whose torque is given as :
$τ = (I l B) \times b sin θ = I (l b) B sin θ = I A B sin θ$
where $A = I b$ = area of the loop. If instead of a single loop, we have a rectangular coil having N turns, then
torque $τ = N I A B sin θ$
In vector notation $\to τ = N I (\to A \times \to B) = (\to m \times \to B)$ , where $\to m = N I \to A$ = magnetic moment of current carrying coil.

Updated on:21/07/2023