A rectangular block of metal of resistivity has dimensions . A potential difference is applied between two opposite faces of the block.
(a) To which two faces of the block should the potential difference be applied to give the maximum current density? What is the maximum current density?
(b) To which two faces of the block should the potential difference be applied to give the maximum current? What is this maximum current?
The correct Answer is:A, B, C, D
To solve the problem, we will break it down into two parts as specified in the question.
Part (a): Maximum Current Density
1. Understanding Current Density:
The current density J is defined as:
J=IA
where I is the current and A is the cross-sectional area through which the current flows.
2. Using Ohm's Law:
According to Ohm's Law, the current I can be expressed as:
I=VR
where V is the potential difference and R is the resistance.
3. Resistance of the Block:
The resistance R of the block can be calculated using:
R=ρLA
where ρ is the resistivity, L is the length of the block in the direction of current flow, and A is the cross-sectional area.
4. Substituting Resistance into Current Density:
Substituting R into the equation for current density:
J=IA=VR⋅A=V⋅AρL
5. Finding the Dimensions:
The dimensions of the block are d×2d×3d. Depending on which faces the potential difference V is applied, the length L will vary:
- If V is applied across the faces of area 2d×3d, then L=d.
- If V is applied across the faces of area d×3d, then L=2d.
- If V is applied across the faces of area d×2d, then L=3d.
6. Maximizing Current Density:
Since J is inversely proportional to L, to maximize J, we need to minimize L. The minimum length L is d.
7. Calculating Maximum Current Density:
Using L=d:
Jmax=Vρd
Therefore, the potential difference should be applied across the faces of area 2d×3d.
Part (b): Maximum Current
1. Using Current Formula:
From Ohm's Law, we have:
I=VR
Substituting for R:
I=V⋅AρL
2. Maximizing Current:
To maximize I, we need to maximize the area A and minimize the length L.
- The maximum area A is 2d×3d=6d2.
- The minimum length L is d.
3. Calculating Maximum Current:
Substituting these values into the equation:
Imax=V⋅(2d⋅3d)ρd=6Vd2ρd=6Vdρ
Summary of Solutions:
- (a) The potential difference V should be applied across the faces of area 2d×3d for maximum current density, which is:
Jmax=Vρd
- (b) The potential difference V should be applied across the faces of area 2d×3d for maximum current, which is:
Imax=6Vdρ
The current density J is defined as:
J=IA
where I is the current and A is the cross-sectional area through which the current flows.
According to Ohm's Law, the current I can be expressed as:
I=VR
where V is the potential difference and R is the resistance.
The resistance R of the block can be calculated using:
R=ρLA
where ρ is the resistivity, L is the length of the block in the direction of current flow, and A is the cross-sectional area.
Substituting R into the equation for current density:
J=IA=VR⋅A=V⋅AρL
The dimensions of the block are d×2d×3d. Depending on which faces the potential difference V is applied, the length L will vary:
- If V is applied across the faces of area 2d×3d, then L=d.
- If V is applied across the faces of area d×3d, then L=2d.
- If V is applied across the faces of area d×2d, then L=3d.
Since J is inversely proportional to L, to maximize J, we need to minimize L. The minimum length L is d.
Using L=d:
Jmax=Vρd
Therefore, the potential difference should be applied across the faces of area 2d×3d.
From Ohm's Law, we have:
I=VR
Substituting for R:
I=V⋅AρL
To maximize I, we need to maximize the area A and minimize the length L.
- The maximum area A is 2d×3d=6d2.
- The minimum length L is d.
Substituting these values into the equation:
Imax=V⋅(2d⋅3d)ρd=6Vd2ρd=6Vdρ
- (a) The potential difference V should be applied across the faces of area 2d×3d for maximum current density, which is:
Jmax=Vρd
- (b) The potential difference V should be applied across the faces of area 2d×3d for maximum current, which is:
Imax=6Vdρ
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Single Correct
26 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 More Than One Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE_TYPE
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
When a potential difference is applied across, the current passing through
View SolutionIf the potential difference V applied to the coolidge tube is doubled, then the cut off wavelength
View SolutionIn the arrangement shown, a potential difference is applied between points A and B. No capacitor can withstand a potential difference of more than 100 V
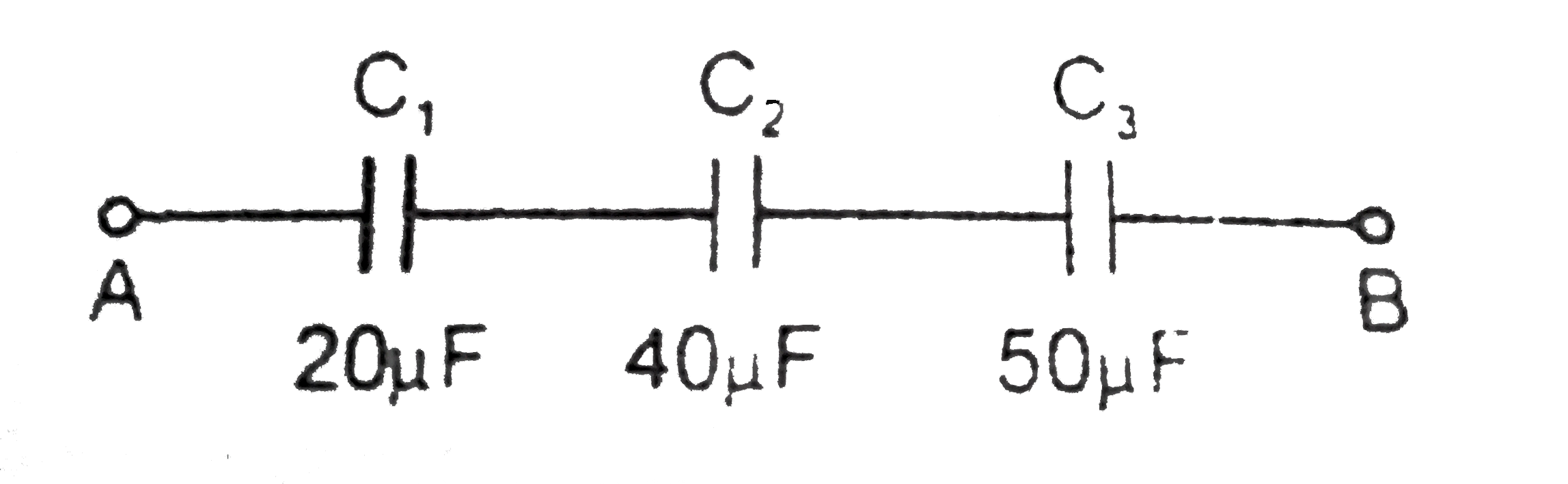
View SolutionWhat is meant by saying that the potential difference between two points is 1V ?
View SolutionA potential difference of 6V is applied to a coil of inductance 0.5H and a resistance of 4 ohm connected in series. The time taken for the current to reach half the maximum value is (in seconds)
View SolutionIf 100 volts of potential difference is applied between a and b in the circuit of , find the potential difference between candd.
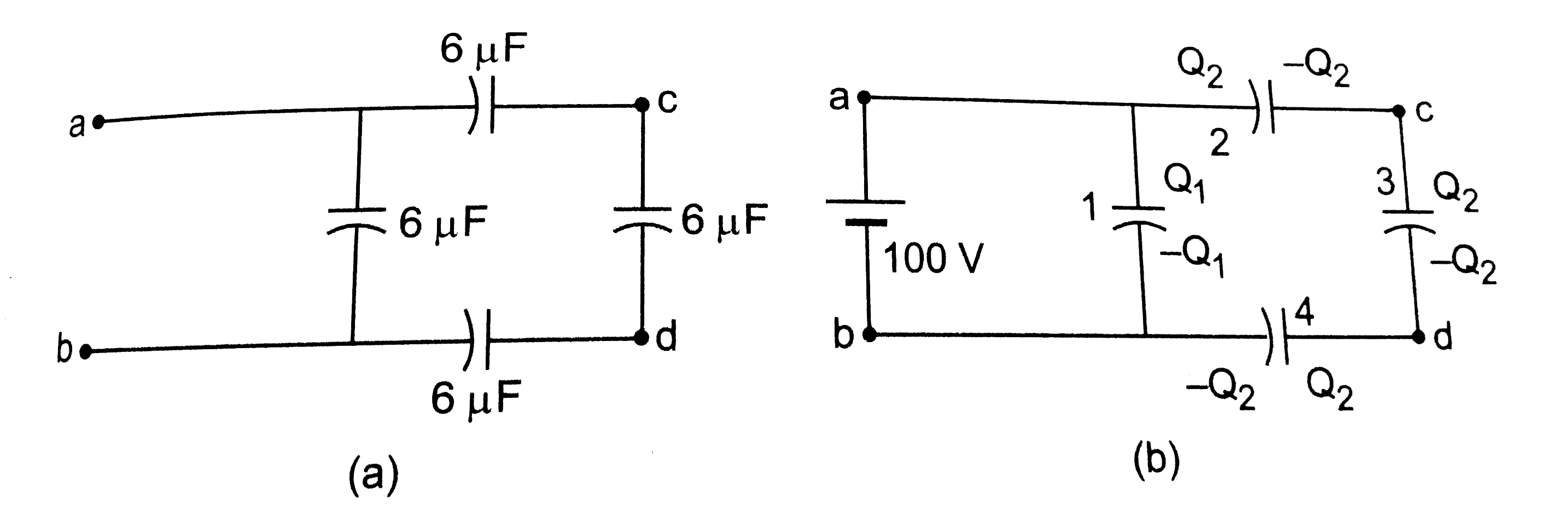
View SolutionHow are the potential difference (V), current (I) and resistance (R) related ?
View SolutionThe potential difference between the terminals of an electric heater is 60V when it draws a current of 4A from the source. What current will the heater draw if the potential difference is increased to 120V ?
View SolutionTwo plates are 2cm apart, a potential difference of 10 volt is applied between them, the electric field between the plates is
View SolutionA parallel plate air capacitor has capcity C distance of separtion between plates is d and potential difference V is applied between the plates force of attraction between the plates of the parallel plate air capacitor is
View Solution
