Two heaters designed for the same voltage V have different power ratings. When connected individually across as source of voltageV, they produce H amount of heat each in time t1 and t2 respectively. When used together acros the same source, they produce H amount of heat in time t
if they are in series t=t1+t2
if they are in series t=2(t1+t2)
if they are in parallel t=t1t2(t1+t2)
if they are in parallel t=t1t22(t1+t2)
The correct Answer is:A, C
To solve the problem, we need to analyze the situation where two heaters are connected individually and then together, and derive the relationships between the time taken to produce a certain amount of heat in different configurations (series and parallel).
1. Understanding Power and Heat Production:
- The power of the first heater (P1) when connected to voltage V is given by:
P1=V2R1
- The power of the second heater (P2) is:
P2=V2R2
- The heat produced by each heater in time t1 and t2 respectively is given by:
H=P1⋅t1andH=P2⋅t2
2. Expressing Resistance in Terms of Heat:
- Rearranging the heat equations gives:
R1=V2H⋅t1andR2=V2H⋅t2
3. Connecting Heaters in Series:
- When the heaters are connected in series, the equivalent resistance Req is:
Req=R1+R2
- The heat produced when both heaters are connected in series for time t is:
H=V2Req⋅t
- Substituting for Req:
H=V2R1+R2⋅t
4. Substituting for R1 and R2:
- Substitute R1 and R2 from the earlier equations:
H=V2(V2Ht1+V2Ht2)⋅t
- Simplifying gives:
H=H⋅tt1+t2
- Thus, we find:
t1+t2=t
5. Connecting Heaters in Parallel:
- When connected in parallel, the equivalent resistance is given by:
1Req=1R1+1R2
- The heat produced in time t is:
H=V2Req⋅t
- Substituting for R1 and R2:
H=V2(HV2⋅1t1+HV2⋅1t2)⋅t
- Simplifying gives:
H=H⋅tt1t2t1+t2
- Thus, we find:
1t=1t1+1t2ort=t1t2t1+t2
Final Results:
- When connected in series: t1+t2=t
- When connected in parallel: t=t1t2t1+t2
- The power of the first heater (P1) when connected to voltage V is given by:
P1=V2R1
- The power of the second heater (P2) is:
P2=V2R2
- The heat produced by each heater in time t1 and t2 respectively is given by:
H=P1⋅t1andH=P2⋅t2
- Rearranging the heat equations gives:
R1=V2H⋅t1andR2=V2H⋅t2
- When the heaters are connected in series, the equivalent resistance Req is:
Req=R1+R2
- The heat produced when both heaters are connected in series for time t is:
H=V2Req⋅t
- Substituting for Req:
H=V2R1+R2⋅t
- Substitute R1 and R2 from the earlier equations:
H=V2(V2Ht1+V2Ht2)⋅t
- Simplifying gives:
H=H⋅tt1+t2
- Thus, we find:
t1+t2=t
- When connected in parallel, the equivalent resistance is given by:
1Req=1R1+1R2
- The heat produced in time t is:
H=V2Req⋅t
- Substituting for R1 and R2:
H=V2(HV2⋅1t1+HV2⋅1t2)⋅t
- Simplifying gives:
H=H⋅tt1t2t1+t2
- Thus, we find:
1t=1t1+1t2ort=t1t2t1+t2
- When connected in series: t1+t2=t
- When connected in parallel: t=t1t2t1+t2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type2videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective13videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Single Correct26videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
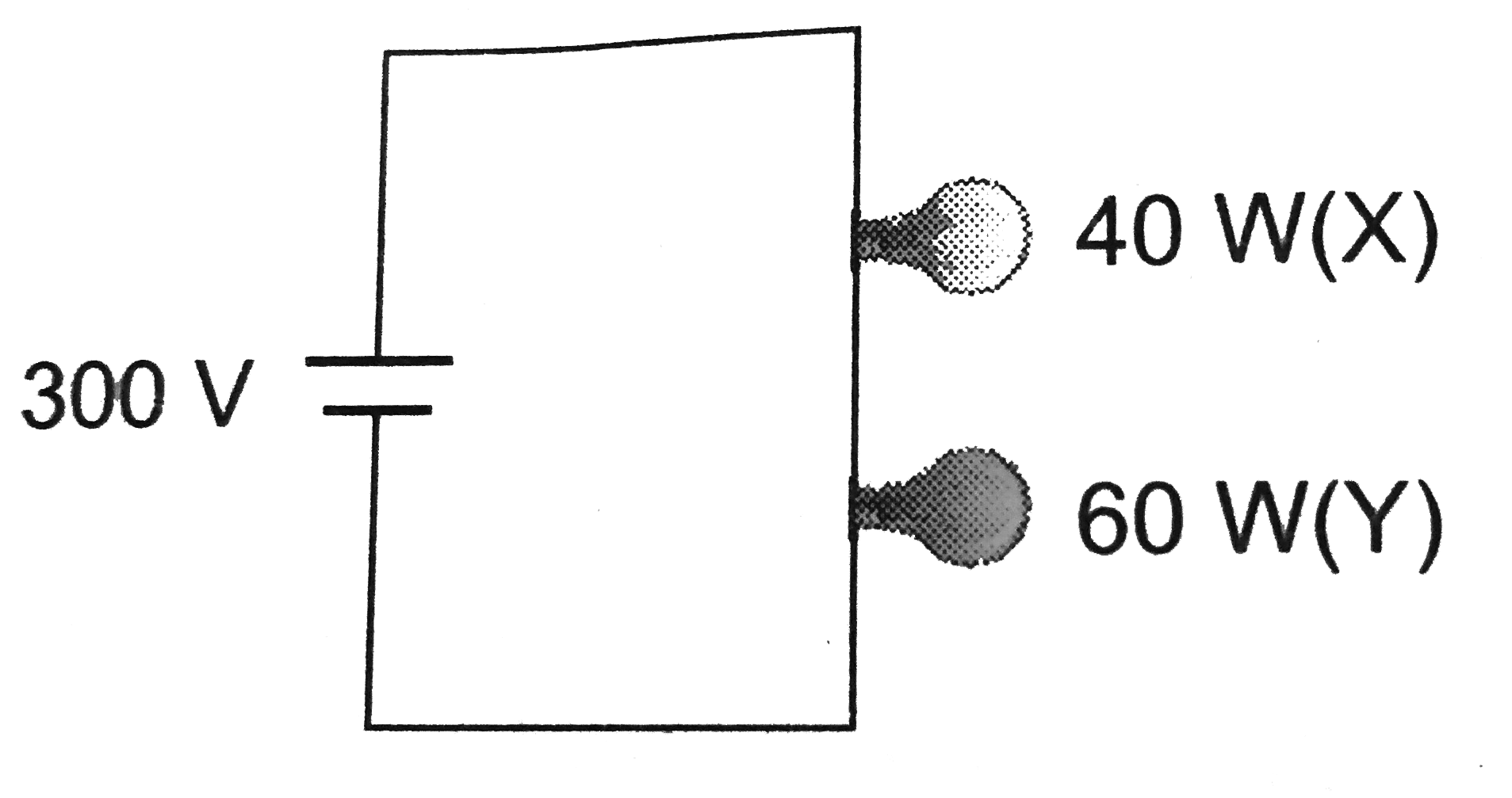
Two bulbs X and Y having same voltage rating and of power 40 watt and 60 watt respectively are connected in series across a potential difference of 300 volt, then
 View Solution
View SolutionTwo wires of the same material and having the same uniform area of cross section are connected in an electric circuit. The masses of the wires are mand2m, respectively. When a current I flows through both of them connected in series, then find the ratio of heat produced in them in a given time .
View SolutionTwo bulbs consume same energy when operated at 200Vand300V , respectively . When these bulbs are connected in series across a dc source of 500V, then
View SolutionA cricket ball thrown across a field is a heights h1 and h2 from the point of projection at time t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
View SolutionTwo bulbs consume the same power when operated at 200 V and 300 V respectively. When these bulbs are connected in series across a DC source of 400 V, then the ratio of power consumed across them is
View SolutionA cell to emf. E and internal resistance r supplies currents for the same time t through external resistanceR1andR2 respectively. If the heat produced in both cases is the same, then the internal resistance is given by :
View SolutionTwo wires 'A' and 'B' of the same material have their lengths in the ratio 1:2 and radii in the ratio 2:1 The two wires are connected in parallel across a battery. The ratio of the heat produced in 'A' to the heat produced in 'B' for the same time is
View SolutionTwo heater wires, made of the same material and having the same length and the same radius, are first connected in series and then in parallel to a constant potential difference. If the rate of heat produced in the two cases are Hs and Hp respectively then HsHp will be
View SolutionWhen an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
View SolutionWhen an alternating voltage of 220V is applied across a device P, a current of 0.25A flows through the circuit and it leads the applied voltage by a angle π2 radian. When the same voltage source is connected across another device Q, the same current is observed in the circuit but in phase with the applied voltage. What is the current when the same source is connected across a series combination of P and Q?
View Solution

