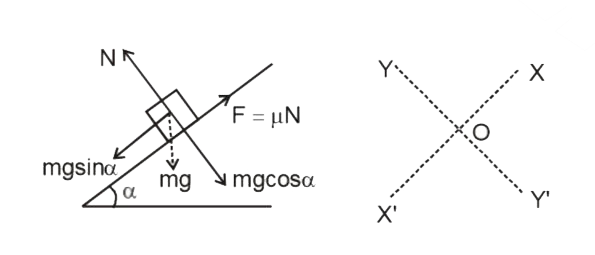
A rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is μ. Let the mass of the box be m.
(a) At what angle of inclination 0 of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane, if the angle of inclination of the plane is increased to a>θ
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?Solution in Gujrati
Consider diagram shown in figure

(a ) For bx just starts to sliding down slope
f=mgsinθ
N=mgcosθ
fN=tanθ
μ=tanθ
θ=tan−1(μ)
( b) When angle of inclination increased to
α>θ
Resultant force be F1
F1=mgsinα−f
(c ) To keep box stationary or moving with uniform speed upward force ir required Here friction force would bed in downward direction
(d ) When box is to be moved with acceleration a upward along the plane net force be F3
friction would be in downward direction
F3=mg(sinα+μcosα)+ma
Topper's Solved these Questions
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - SECTION -E(MULTIPLE CHOICE QUESTIONS) (MCQS)
69 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - SECTION-F (QUESTIONS FROM MODULE)
22 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - SECTION-C(OBJECTIVE QUESTIONS) (VSQS)
55 Videos
- GRAVITATIONBOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - QUESTIONS PAPER Section - D
1 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - QUESTION PAPER
11 Videos
Similar Questions
The position (x) → time (t) graph of one dimensional motion of a body of mass 0.4 kg. What is the magnitude of impulse of force

View SolutionA block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block ((in kg) is .......... (Take g = 10 m/s2)
View SolutionArea of F → t graph gives which physical quantity ?
View SolutionA spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system ? Mass of the spaceship = 1000 kg, mass of the sun =2×1030kg, mass of mars =6.4×1023kg, radius of mars = 3395 km, radius of the orbit of mars =2.28×108km,G=6.67×10−11Nm2kg2
View SolutionWhat is called brittle material ?
View SolutionA rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionA box of mass 4kg rests upon an inclined plane This inclination is gradually incresed till the box starts sliding down the plane. At this stage slope of the plane is 1 in 3 Find coefficient of friction between the box and the plane What force applied to the box parallel to the plane will just make the box move up the plane ?
View SolutionA wooden box of mass 8kg slides down an inclined plane of inclination 30^(@) to the horizontal with a constant acceleration of 0.4ms^(-2) What is the force of friction between the box and inclined plane ? (g = 10m//s^(2)) .
View SolutionA rectangular box lies on a rough inclined surface The co-efficient of friction beteen the surface and the box is mu . Le the mass of the box ne m What is the force acting on the box down the plane if the angle of inclination of the plane is increased to alpha gt theta ? .
View SolutionA box is lying on an inclined plane what is the coefficient of static friction if the box starts sliding when an angle of inclination is 60∘
View SolutionA rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is mu . Let the mass of the box be m . (a) At what angle of inclination theta of the plane to the horizontal will the box just start to slide down the plane ? (b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to alpha gt theta ? (c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ? (d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionA 20kg box is gently placed on a rough inclined plane of inclination 30∘ with horizontal. The coefficient of sliding friction between the box and the plane is 0.5.Find the acceleration of the box down the incline.
View SolutionA rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is (μ) Let the mass of the box be m.
At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
View SolutionA rectangular box lies on a rough inclined surface The co-efficient of friction beteen the surface and the box is μ. Le the mass of the box ne m What is the force acting on the box down the plane if the angle of inclination of the plane is increased to α>θ ? .
View SolutionA box is lying on an inclined plane if the box slides when the angle of inclination is 60^(@) then the coefficient of static friction of the box and the plane is?
View Solution
