A rectangular coil of 100 turns has length 5 cm and width 4 cm. it is placed with its plane parallel to a uniform magnetic field and a current of 2 A is sent through the coil. Find the magnitude of the magnetic field B, if the torque acting on the coil is 0.2Nm−1.
To solve the problem, we need to find the magnitude of the magnetic field B acting on a rectangular coil given the torque τ, number of turns N, current I, length l, and width w of the coil.
1. Identify Given Values:
- Number of turns, N=100
- Length of the coil, l=5cm=0.05m
- Width of the coil, w=4cm=0.04m
- Current, I=2A
- Torque, τ=0.2Nm
2. Calculate the Area A of the Coil:
A=l×w=0.05m×0.04m=0.002m2
3. Use the Formula for Torque:
The formula for torque τ acting on a coil in a magnetic field is given by:
τ=N⋅I⋅B⋅A⋅sin(θ)
Since the plane of the coil is parallel to the magnetic field, the angle θ=90∘, and sin(90∘)=1. Therefore, the equation simplifies to:
τ=N⋅I⋅B⋅A
4. Rearranging the Formula to Solve for B:
We can rearrange the equation to find B:
B=τN⋅I⋅A
5. Substituting the Known Values:
Now, substitute the known values into the equation:
B=0.2Nm100⋅2A⋅0.002m2
6. Calculating B:
B=0.2100⋅2⋅0.002=0.20.4=0.5T
Final Answer:
The magnitude of the magnetic field B is 0.5T.
- Number of turns, N=100
- Length of the coil, l=5cm=0.05m
- Width of the coil, w=4cm=0.04m
- Current, I=2A
- Torque, τ=0.2Nm
A=l×w=0.05m×0.04m=0.002m2
The formula for torque τ acting on a coil in a magnetic field is given by:
τ=N⋅I⋅B⋅A⋅sin(θ)
Since the plane of the coil is parallel to the magnetic field, the angle θ=90∘, and sin(90∘)=1. Therefore, the equation simplifies to:
τ=N⋅I⋅B⋅A
We can rearrange the equation to find B:
B=τN⋅I⋅A
Now, substitute the known values into the equation:
B=0.2Nm100⋅2A⋅0.002m2
B=0.2100⋅2⋅0.002=0.20.4=0.5T
The magnitude of the magnetic field B is 0.5T.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
A tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionA rectangular coil of dimensions 4 cm x 5 cm with number of turns 20 is placed with its plane perpendicular to a uniform magnetic field of 5 T. If it is moved with a speed of 2 m/s in the field parallel to its length, the e.m.f induced is
View Solution
Knowledge Check
- Question 1 - Select One
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 Nm
A 100 turns coil shown in figure carries a current of 2 amp in a magnetic field B=0.2Wb/m2. The torque acting on the coil is
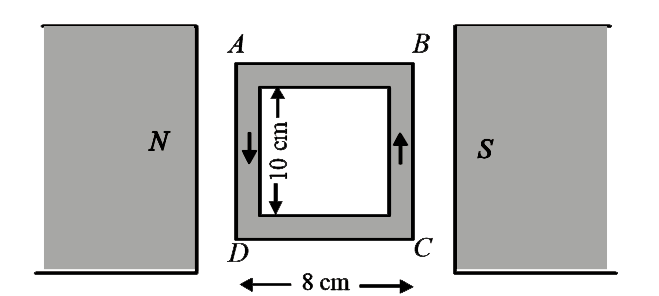 View Solution
View SolutionIf plane of coil and uniform magnetic field B(4T0 is same then torque on the current carrying coil is
 View Solution
View SolutionA coil carrying electric current is placed in uniform magnetic field
View SolutionA closed coil consists of 500 turns has area 4cm2 and a resistance of 50Ω. The coil is kept with its plane perpendicular to a uniform magnetic field of 0.2Wbm2. Calculate the amount charge flowing through the coil if it is rotated through 180∘
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA coil of area 5cm2 and having 20 turns is placed in a uniform magnetic field of 103 gauss. The normal to the plane of the coil makes an angle of 60∘ with the magnetic field. The flux in Maxwell through the coil is:
View Solution

