A rectangular vessel of dimension (l×b×h) and mass M contains a liquid of density ρ. The vessel has an orifice at its bottom at a distance c from the rear wall as shown in the figure.

The maximum volume of the water that can be stored when the vessel is accelerated is hcb/2
The maximum volume of the water that can be stored when the vessel is accelerated is hlb/2
Force F that must he applied when maximum water stored is [M+hcbρ2]hgc
Force F that must be applied when maximum water stored is [M+hcbρ2]lgc
The correct Answer is:A, C
The maximum amount of water that can be retained is shown in the figure. If θ is the angle made by the water suface with the horizontal then
tanθ=hc=ag⇒a=hgc
So the maximum volume that can be retained is (12)×h×c×b and F=[M+hcbρ2]hgc

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
The force F needed to support the liquid of density ρ and the vessel on it, in figure, is
View SolutionThere is one cylindrical vessel whose height and diameter are both equal to D. An observer's eye is placed in such a manner that bottom edge of the vessel is just visible to eye.

There is a point P at the bottom of container at a distance x from the centre of container as shown in the figure. Up to what height the liquid of refractive index μ should be poured in the vessel so that point P is visible to the eye?View Solution
Knowledge Check
- Question 1 - Select One
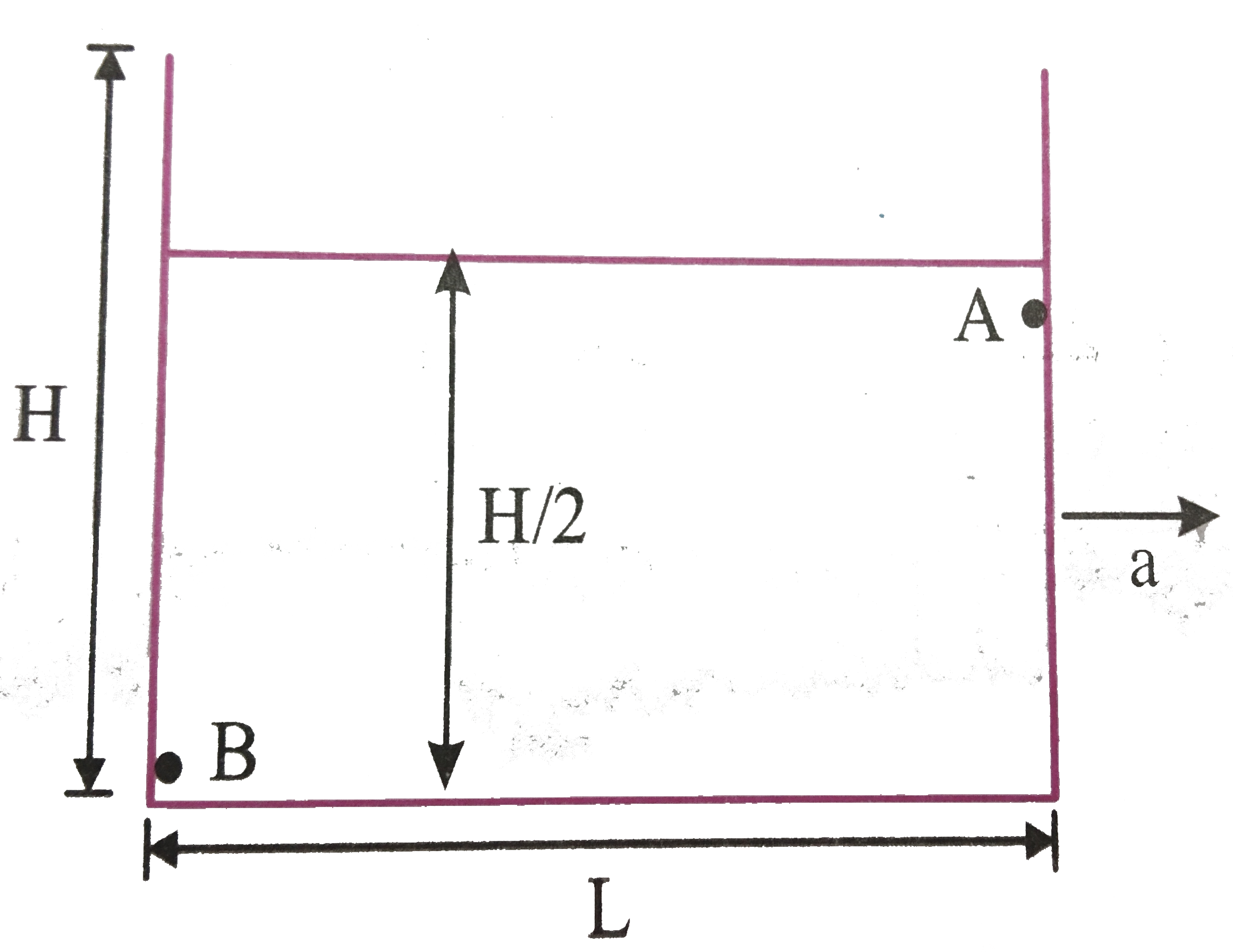
A vessel of height H and length L contains a liquid of density ρ upto height H/2 The vessel start accelerating horizontally with acceleration a towards right. If A is the point at the surface of the liquid at right . If A is the point at the surface of the liquid at right end while the vessel is accelerating and B is the point at bottom of the vessel on the other end, the difference of pressures at B and A will beAρ2(gH+aL)Bρ2(gH−aL)C2ρ(gH−aL)D3ρ2(gH+aL) - Question 2 - Select One
A container shown in figure contains a liquid to depth H, and of density ρ The gauge pressure at point P is :
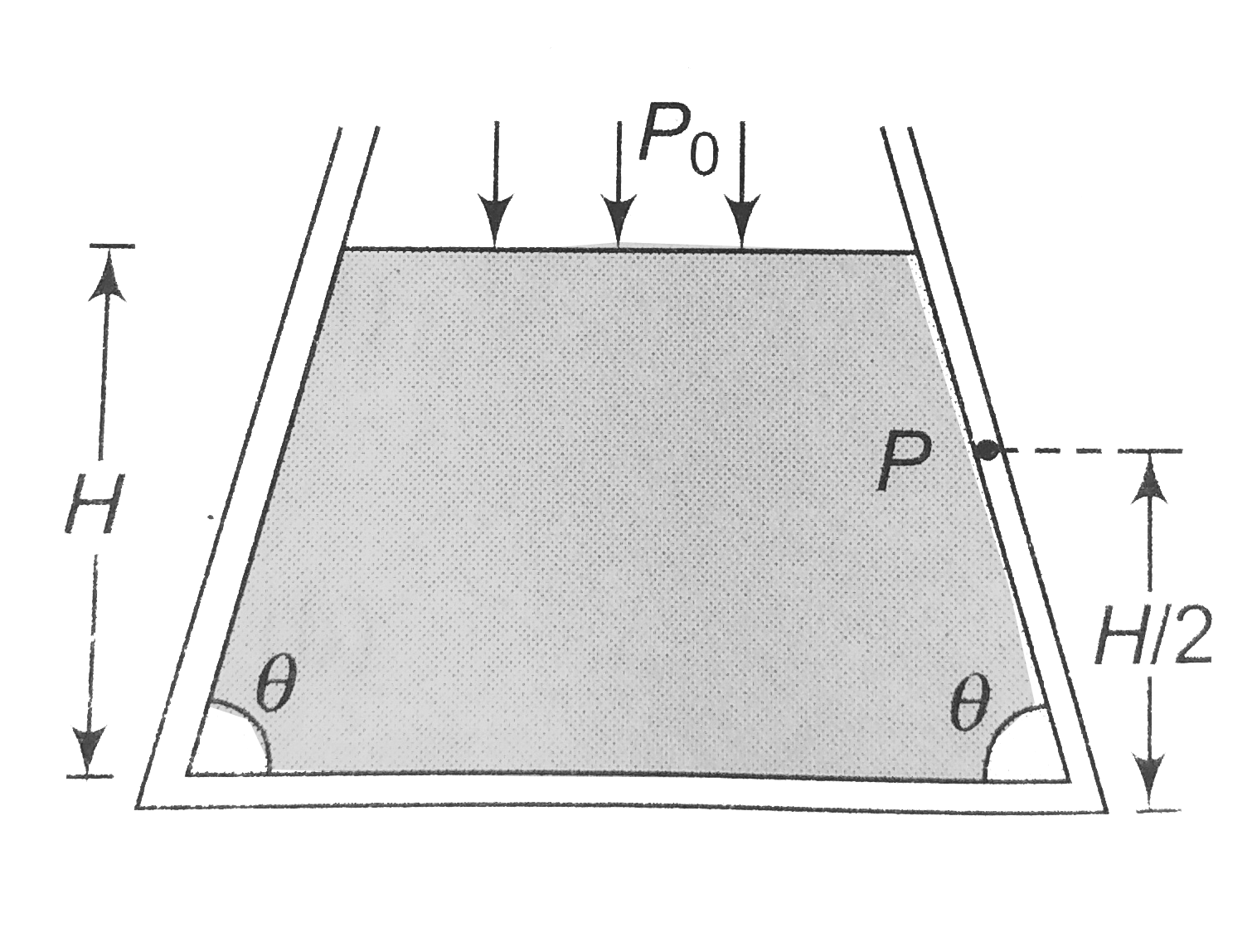 AρgH2+P0BρgH2CρgH2cosθDρgHcosθ2
AρgH2+P0BρgH2CρgH2cosθDρgHcosθ2 - Question 3 - Select One

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρa
A rectangular vessel of dimensions 20cm×16cm×11cm . is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height. [Use π=22/7 ]
View SolutionA lipuid is poured into a cylindrical vessel of height H and mass M. to what height a liquid of density p should be poured so that the centre of gravity of the vessel + kuqyud ' sustem mat be at the minimum height from the bottom . Negalect the mass of the bottom .the area of cross - section of the vessel of A .
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA rectangular vessel when full of water takes 10 minutes to be emptied through an orifice in its bottom. How much time will it take to be emptied when half filled with water
View SolutionTwo identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid height is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View Solution

