Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density $ρ$ . The area of either base is A but in one vessel the liquid height is $h_{1}$ and in the other liquid height is $h_{2} (h_{2} < h_{1})$ . If the two vessel are connected, the work done by gravity in equalizing the level is

A

$\frac{1}{2} {(h_{1} - h_{2})}_{1}^{2} A ρ g$

B

$\frac{1}{2} {(h_{1} + h_{2})}_{1}^{2} A ρ g$

C

$\frac{1}{2} {(h_{1}^{2} - h_{2}^{2})}^{2} A ρ g$

D

$\frac{1}{4} {(h_{1} - h_{2})}_{1}^{2} A ρ g$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let $h =$ final height of liquid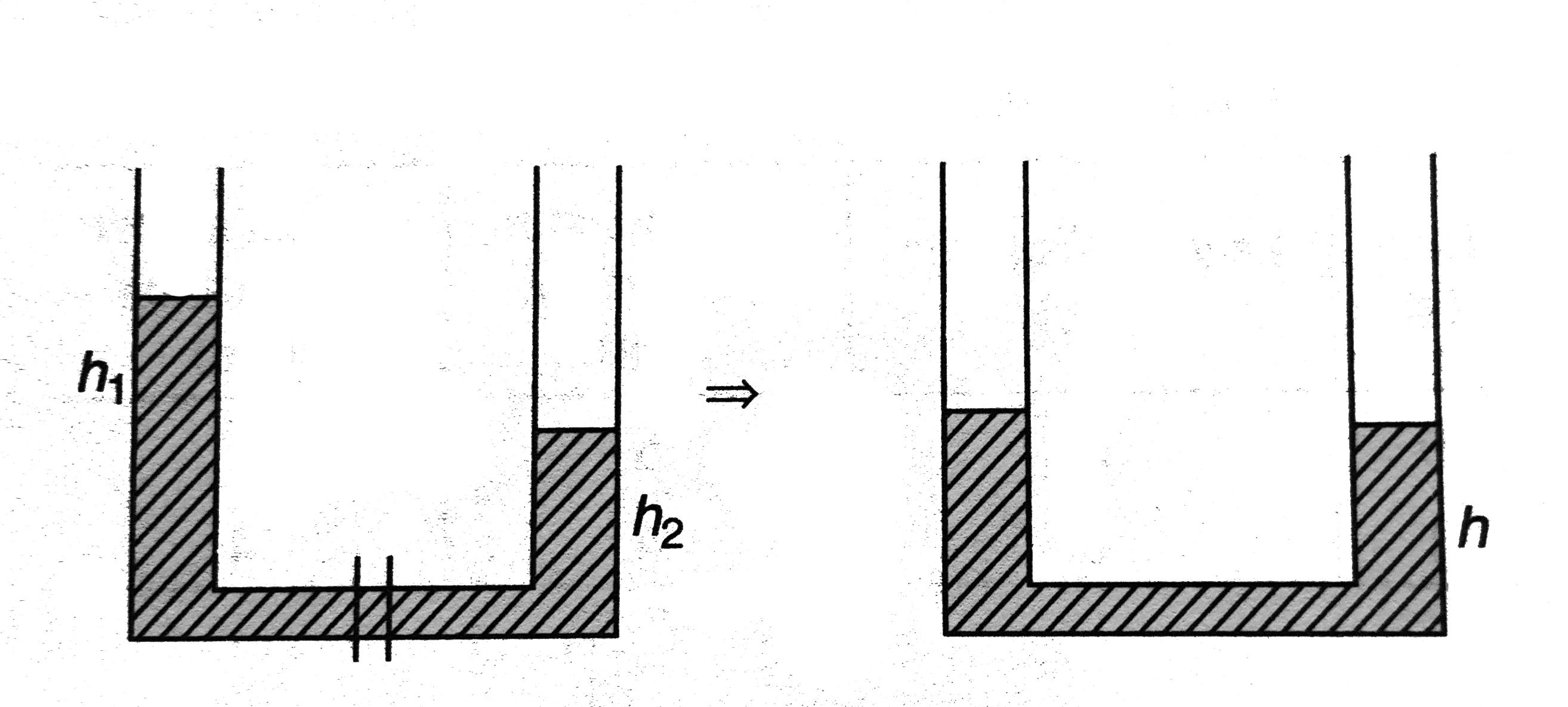
Equanting the volume we have
$A h_{1} + A h_{2} = A (2 h)$
$∴ h = \frac{h_{1} + h_{2}}{2}$
$W_{m g} = - Δ U = U_{i} - U_{f}$
$= [(A h_{1} ρ g . \frac{h_{1}}{2}) + (A h_{2} ρ g . \frac{h_{2}}{2})]$
$- [2 A (\frac{h_{1} + h_{2}}{2}) ρ (\frac{h_{1} + h_{2}}{4})]$
Simplifyig this expression we get the result.

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A liquid of density $ρ$ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is $h_{1}$ and that in the other vessel is $h_{2}$ . If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
A $(h_{1} - h_{2}) g ρ$
B $(h_{1} - h_{2}) g A ρ$
C $\frac{1}{2} {(h_{1} - h_{2})}_{1}^{2} g A ρ$
D $\frac{1}{4} {(h_{1} - h_{2})}_{1}^{2} g A ρ$
Question 2 - Select One
A uniformly tapering vessel is filled with a liquid of density $900 k g / m$ . The force that acts on the base of the vessel due to the liquid is $(g = 10 m s^{- 2})$ (upper area= $10^{- 3} m^{2}$ ,lower area $= 2 \times 10^{- 3} m^{2}$ )

A $3.6 N$
B $7.2 N$
C $9.0 N$
D $14.4 N$
Question 3 - Select One
A uniformly tapering vessel of height h whose lower and upper radii are r and R is completely filled with a liquid of density $ρ$ The force that acts on the base of the vessel due of the liquid is
A $π R^{2} h ρ g$
B $π r^{2} h ρ g$
C $π {(\frac{R + π}{2})}^{2} h ρ g$
D $\frac{1}{3} π (R^{2} - r^{2}) h ρ g$

DC PANDEY-FLUID MECHANICS-Level 2 Single Correct

Home
Ask Doubt
Profile