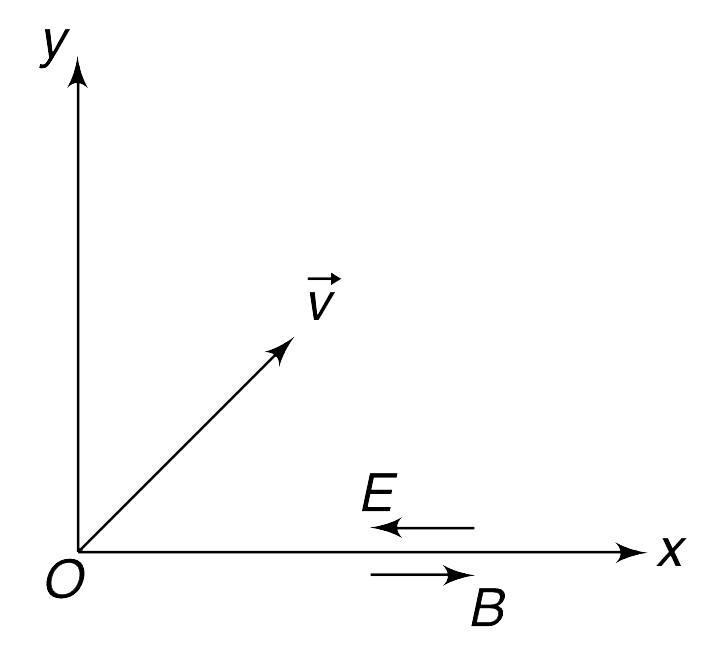
A region has a uniform magnetic field B along positive x direction and a uniform electric field E in negative x direction. A positively charged particle is projected from origin with a velocity −−→V=V0ˆi+V0ˆj . After some time the velocity of the particle was observed to beV0ˆJ while its x co-ordinate was positive. Write all possible values of EB
The correct Answer is:EB=v02πnwheren=1,2,3….
Step by step video, text & image solution for A region has a uniform magnetic field B along positive x direction and a uniform electric field E in negative x direction. A positively charged particle is projected from origin with a velocity underset(V)to=V_(0)hati+V_(0)hatj . After some time the velocity of the particle was observed to beV_(0)hatJ while its x co-ordinate was positive. Write all possible values of (E)/(B) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-2
13 Videos
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-3
4 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
- NUCLEAR PHYSICSBOOK - ARIHANTCHAPTER - NUCLEAR PHYSICSEXERCISE - All Questions
54 Videos
Similar Questions
A uniform electric field,−−→E=E0ˆi and a uniform magnetic field,−−→B=B0ˆi exist in region y>0.A particle hav- ing positive charge q and mass m is projected from the origin with a velocity −−→V=V0ˆi+V0ˆJ. The velocity of the particle when it leaves the region of fields was found to be −−−→V.
(i) Find the ratio E0B0 in terms of v0.
(ii) Find the co-ordinates of the point where the particle leaves the fields.
(iii) Find the minimum speed of the particle during the course of the motion.
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View Solution
Knowledge Check
A proton is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj.
Aits z-coordinate can never be negativeBits x-coordinate can never be negativeCits x-and z-coordinates cannot be zero at the same timeDits y-coordinate will be proportional to its time of flightA uniform electric field →E in the y-direction and uniform magnetic field →B in the x-direction exists in free space. A particle of mass m and carrying charge g is projected from the origin with speed v0 along the y axis. The speed of the particle as a function of its y coordinate will be
A√v20+2qEymB√v20+qEymC√v20+4qEymDv0A charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Pitch of the helical path described by the particle isA2πmv0B0qB√3πmv02B0qCπmv0B0qD2√3πmv0B0q
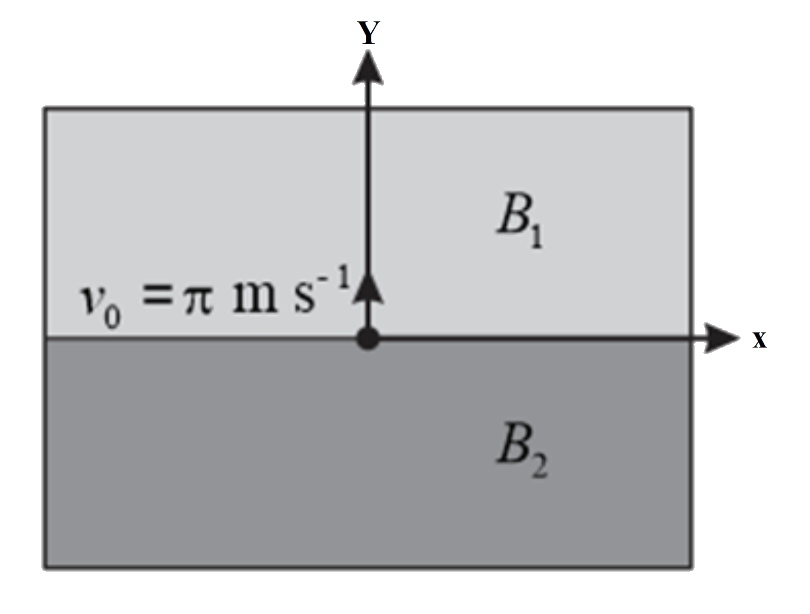
In the XY- plane , the region y>0 has a uniform magnetic field B1ˆk and the region y<0has another uniform magnetic field B2ˆk. A positively charged particle is projected from the origin along the positive y- axis with speed v0=πms−1 at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B2=4B1, the average speed to the particle , in ms−1, along the x- axis in the time interval T is __________ .
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Maximum z-coordinate of the particle is
View SolutionElectric field strength ¯¯¯E=E0ˆi and ¯¯¯B=B0ˆi exists in a region. A charge is projected with a velocity ¯v=v0ˆj at origin , then
View SolutionA projectile is projected from ground with initial velocity →u=u0ˆi+v0ˆj. If acceleration due to gragvity (g) is along the negative y-direction then find maximum displacement in x-direction.
View SolutionElectric field and magnetic field n a region of space is given by E=E0ˆj and B=B0ˆj. A particle of specific charge alpha is released from origin with velocity v=v0ˆi. Then path of particle
View Solution
