A rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of interia is given by
I=2x2−12x+27
The x-coordinate of centre of mass is.
x=2
x=0
x=1
x=3
The correct Answer is:D
To find the x-coordinate of the center of mass of the rigid body, we need to minimize the moment of inertia given by the equation:
I=2x2−12x+27
Step 1: Differentiate the Moment of Inertia
To find the value of x that minimizes the moment of inertia, we take the derivative of I with respect to x:
dIdx=ddx(2x2−12x+27)
Step 2: Apply the Derivative
Using the power rule of differentiation:
dIdx=2⋅2x−12⋅1+0=4x−12
Step 3: Set the Derivative to Zero
To find the critical points, we set the derivative equal to zero:
4x−12=0
Step 4: Solve for x
Now, we solve for x:
4x=12x=124x=3
Conclusion
The x-coordinate of the center of mass is x=3.
To find the value of x that minimizes the moment of inertia, we take the derivative of I with respect to x:
Using the power rule of differentiation:
To find the critical points, we set the derivative equal to zero:
Now, we solve for x:
The x-coordinate of the center of mass is x=3.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Any point on the X-axis is of the form
View SolutionIf a point lies on X-axis, then what are its y and z co-ordinates ?
View SolutionThe tangent at any point P on y2=4x meets x-axis at Q, then locus of mid point of PQ will be
View SolutionFind all the points of local maxima and minima of the function f given by f(x)=4x3−12x2+12x+10
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
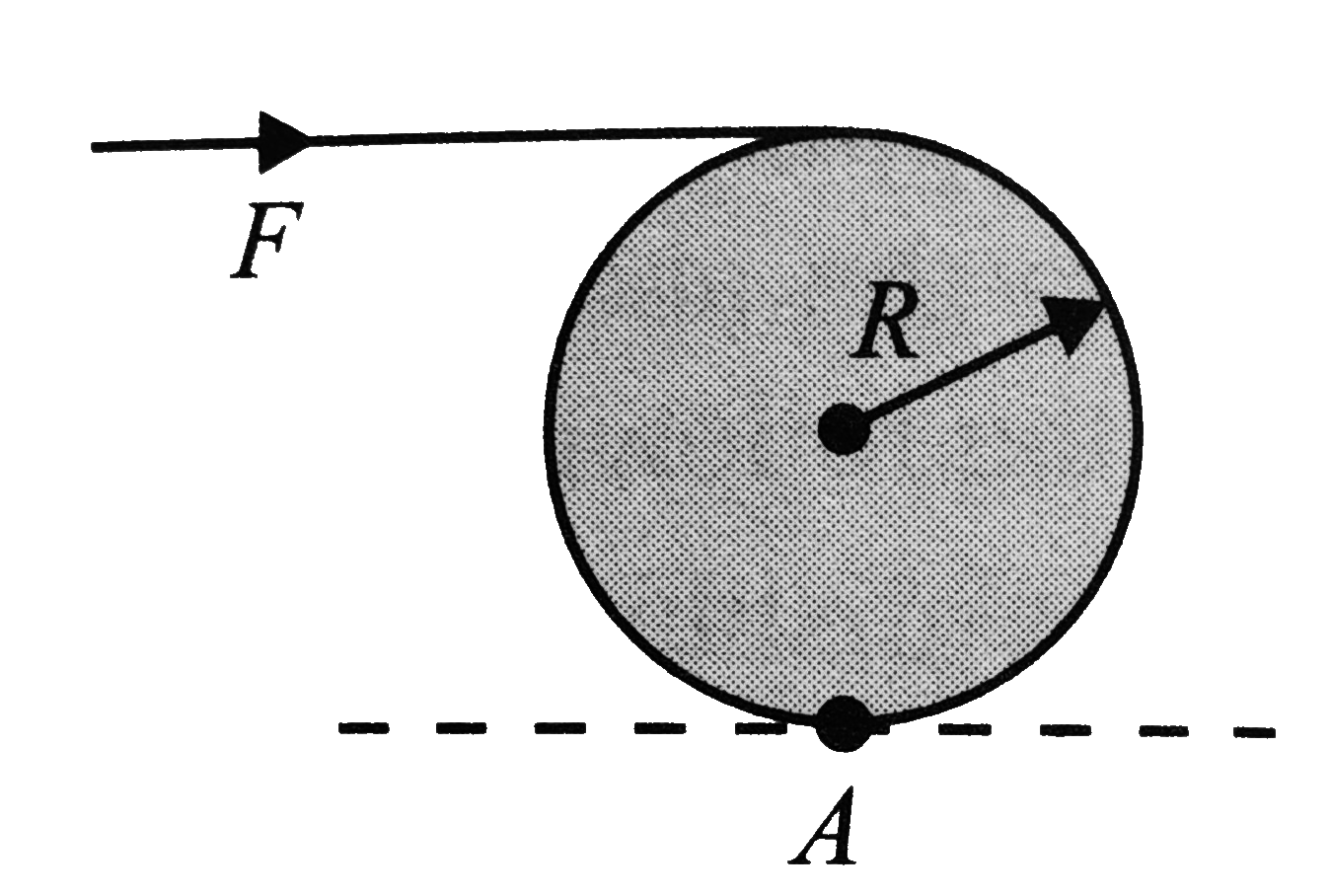
Tangential acceleration of the centre of mass is
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
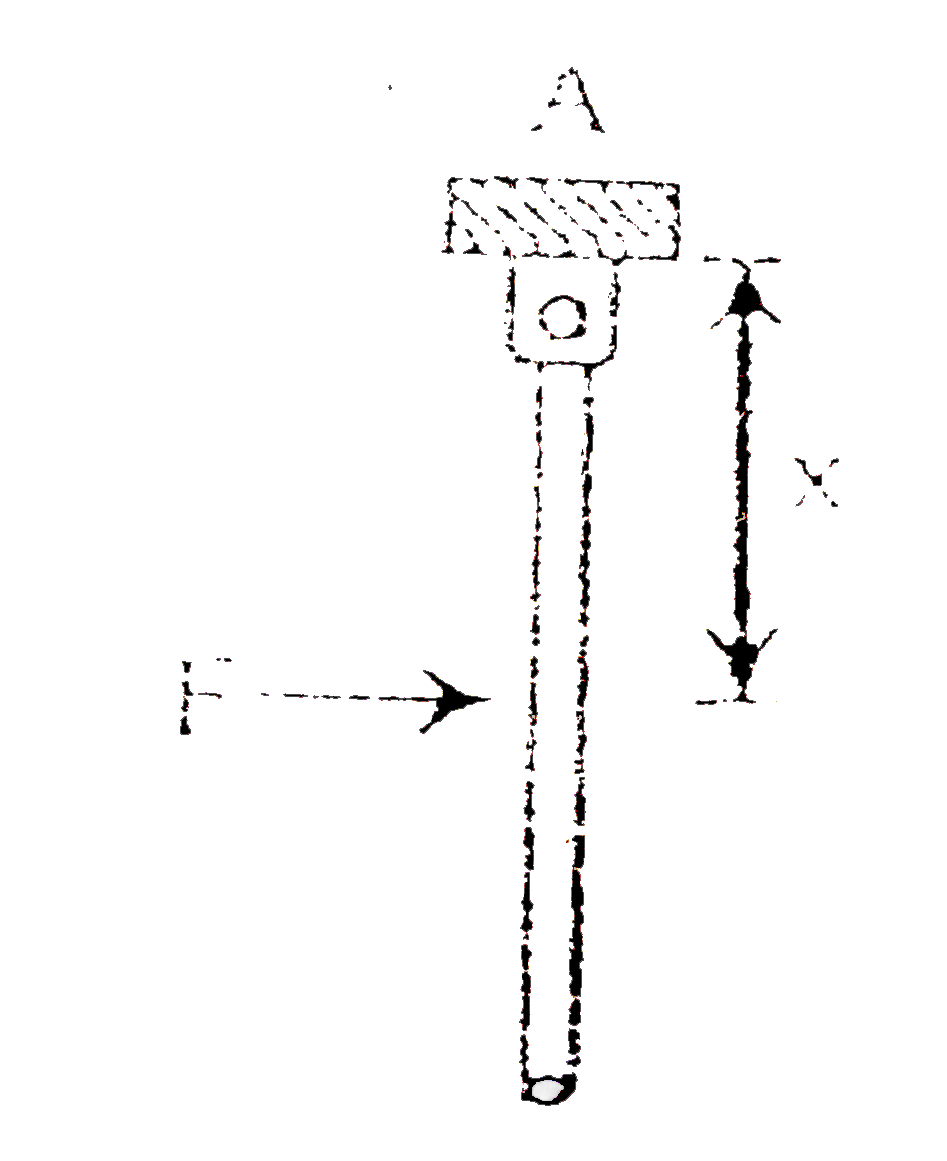
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
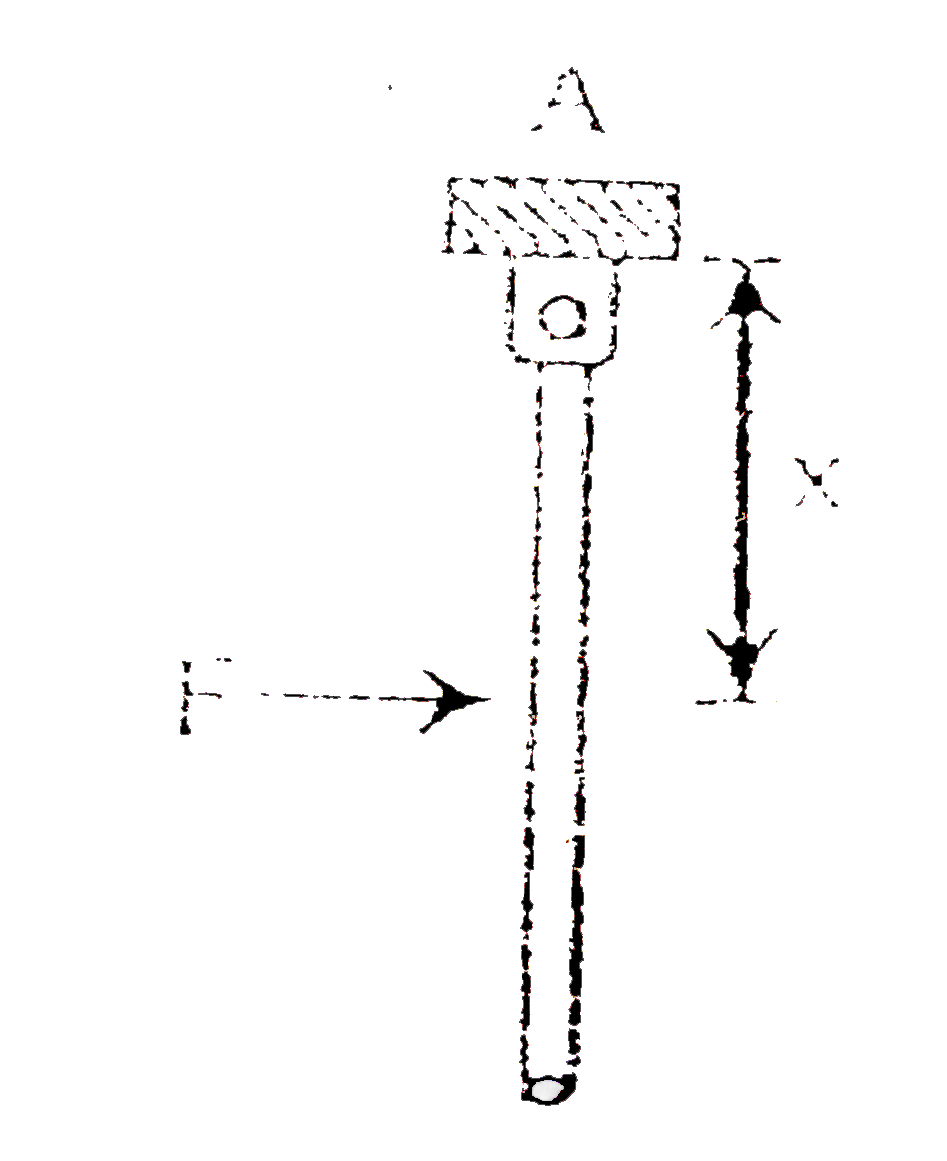
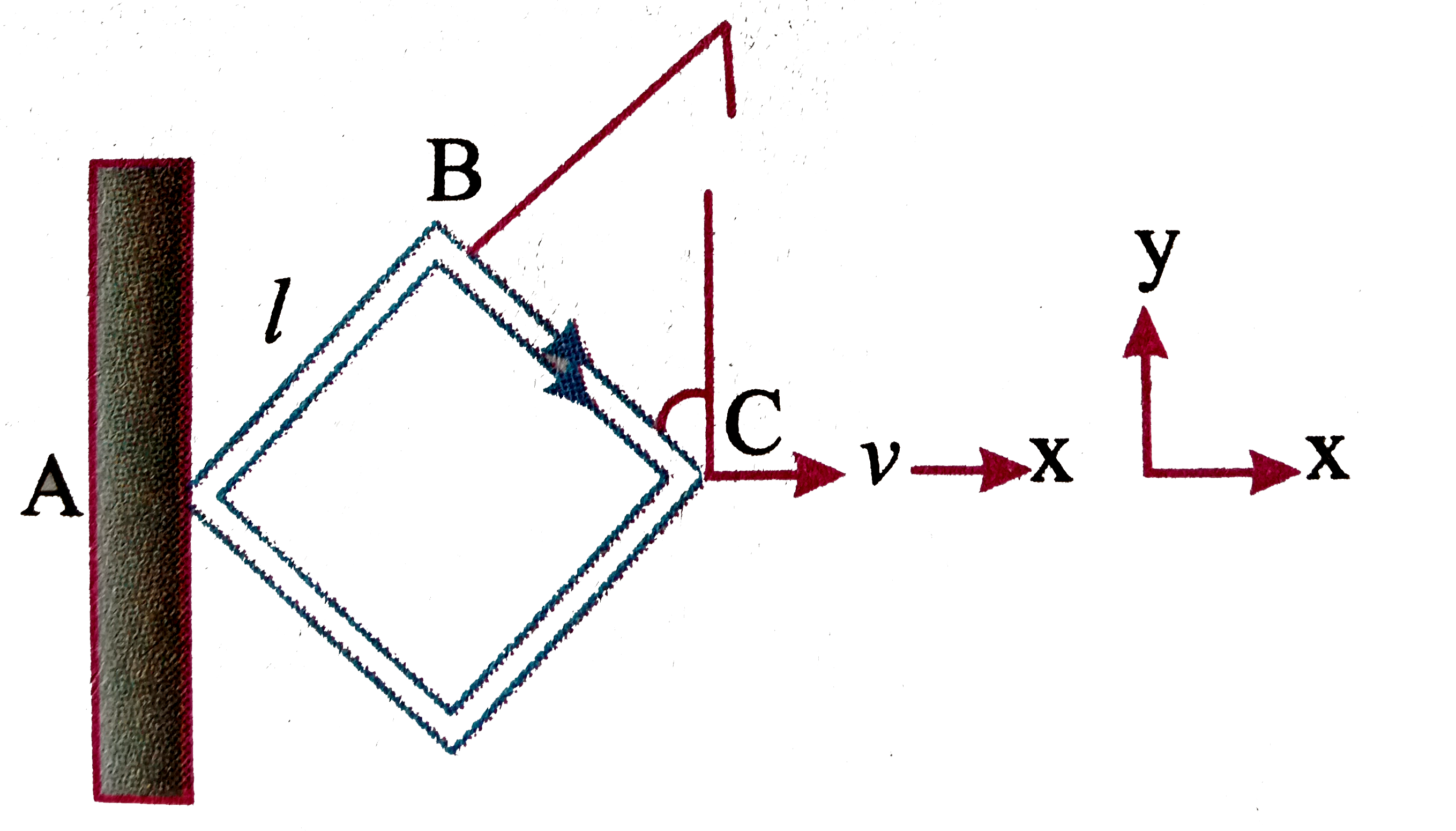
View SolutionFour rods of side length l have been hinged to form a rhombus. Vertex A is fixed to a rigid support, vertex C is being moved along the x-axis with constant velocity V as shown in figure. The rate at which vertex B is nearing the x-axis at the moment the rhombus is in the form of a squarem is
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View Solution
