A ring, cylinder and solid sphere are placed on the top of a rough incline on which the sphere can just roll without slipping. When all of them are released at the same instant from the same position, then
all of them reach the ground at the same instant
the sphere reaches first and the ring at the last
the sphere reaches first and the cylinder and ring reach together
none of the above
The correct Answer is:A
To solve the problem of determining which object (ring, cylinder, or solid sphere) reaches the bottom of a rough incline first when released from the same height, we need to analyze the motion of each object considering both translational and rotational dynamics.
1. Identify Forces Acting on the Objects:
Each object experiences gravitational force acting down the incline (mg sin θ) and frictional force acting up the incline. The frictional force is necessary for rolling without slipping.
2. Set Up the Equations of Motion:
For each object, we can establish the following equations:
- Translational motion: mgsinθ−F=ma
- Rotational motion: F⋅r=I⋅α
Here, F is the frictional force, I is the moment of inertia, r is the radius, a is the linear acceleration, and α is the angular acceleration.
3. Relate Linear and Angular Acceleration:
For rolling without slipping, the relationship between linear acceleration a and angular acceleration α is given by:
a=αr
4. Substitute Angular Acceleration:
From the rotational equation, we can express F in terms of a:
F=I⋅ar2
Substituting this into the translational motion equation gives:
mgsinθ−I⋅ar2=ma
5. Solve for Acceleration a:
Rearranging the equation leads to:
mgsinθ=ma+I⋅ar2
mgsinθ=a(m+Ir2)
Thus, the acceleration a can be expressed as:
a=mgsinθm+Ir2
6. Calculate Moment of Inertia for Each Object:
- Ring: I=mr2
- Cylinder: I=12mr2
- Solid Sphere: I=25mr2
7. Substitute Moments of Inertia:
- For the ring:
aring=mgsinθm+mr2r2=gsinθ1+1=gsinθ2
- For the cylinder:
acylinder=mgsinθm+12mr2/r2=gsinθ1+12=gsinθ32=2gsinθ3
- For the solid sphere:
asphere=mgsinθm+25mr2/r2=gsinθ1+25=gsinθ75=5gsinθ7
8. Compare Accelerations:
- aring=gsinθ2
- acylinder=2gsinθ3
- asphere=5gsinθ7
The order of acceleration from highest to lowest is:
asphere>acylinder>aring
9. Conclusion:
Since the object with the highest acceleration reaches the bottom first, the solid sphere will reach the bottom first, followed by the cylinder, and lastly the ring.
Final Answer:
The order in which they reach the bottom is: Sphere > Cylinder > Ring.
Each object experiences gravitational force acting down the incline (mg sin θ) and frictional force acting up the incline. The frictional force is necessary for rolling without slipping.
For each object, we can establish the following equations:
- Translational motion: mgsinθ−F=ma
- Rotational motion: F⋅r=I⋅α
For rolling without slipping, the relationship between linear acceleration a and angular acceleration α is given by:
a=αr
From the rotational equation, we can express F in terms of a:
F=I⋅ar2
Substituting this into the translational motion equation gives:
mgsinθ−I⋅ar2=ma
Rearranging the equation leads to:
mgsinθ=ma+I⋅ar2
mgsinθ=a(m+Ir2)
Thus, the acceleration a can be expressed as:
a=mgsinθm+Ir2
- Ring: I=mr2
- Cylinder: I=12mr2
- Solid Sphere: I=25mr2
- For the ring:
aring=mgsinθm+mr2r2=gsinθ1+1=gsinθ2
- For the cylinder:
acylinder=mgsinθm+12mr2/r2=gsinθ1+12=gsinθ32=2gsinθ3
- For the solid sphere:
asphere=mgsinθm+25mr2/r2=gsinθ1+25=gsinθ75=5gsinθ7
- aring=gsinθ2
- acylinder=2gsinθ3
- asphere=5gsinθ7
asphere>acylinder>aring
Since the object with the highest acceleration reaches the bottom first, the solid sphere will reach the bottom first, followed by the cylinder, and lastly the ring.
The order in which they reach the bottom is: Sphere > Cylinder > Ring.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


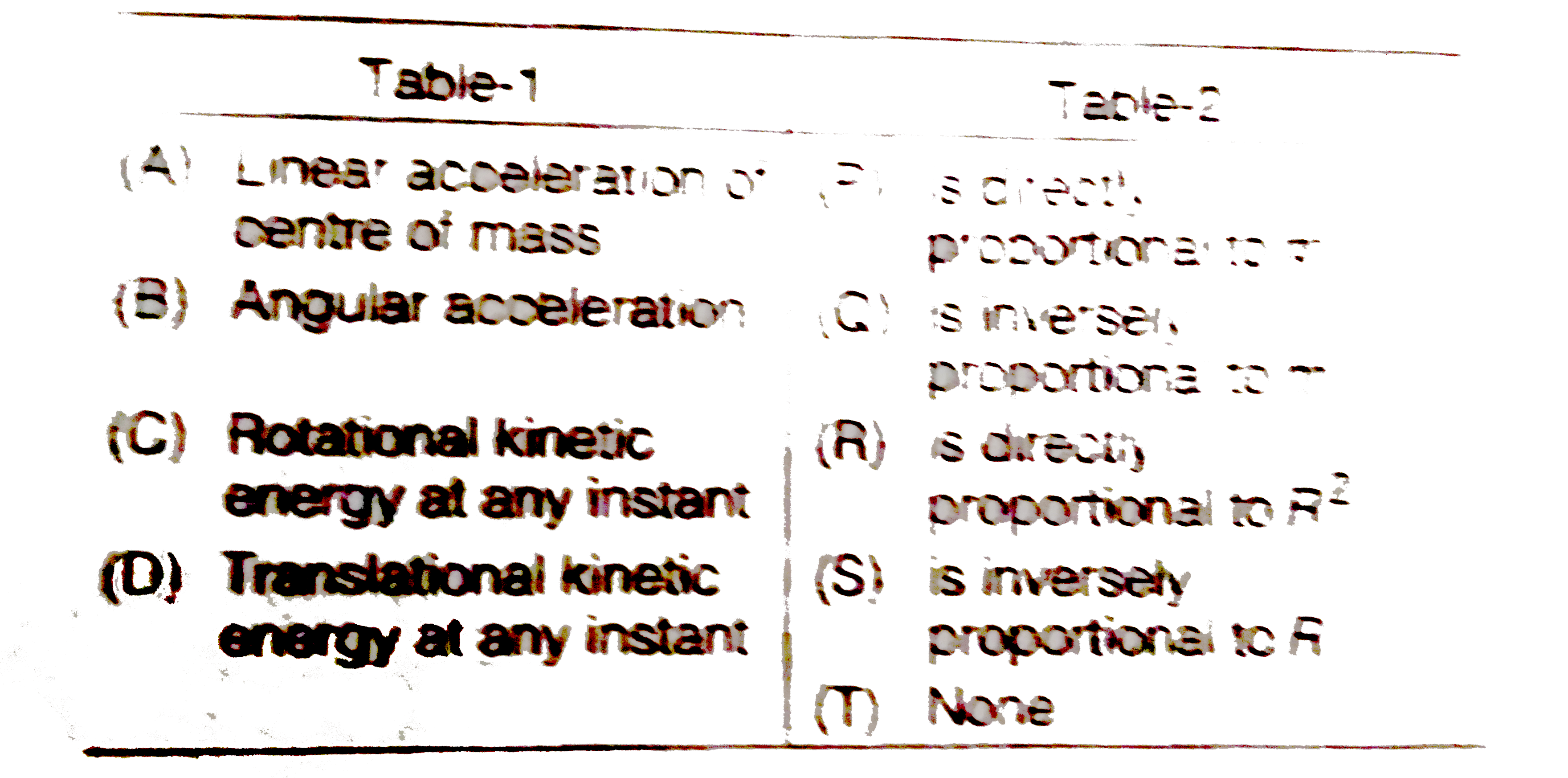 View Solution
View SolutionTwo uniform solid spheres having unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping
View Solution
Knowledge Check
- Question 1 - Select One
Three bodies, a ring, a soild cylinder and a soild sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity ?
ARingBSolid cylinderCSolid sphereDAll reach the ground with same velocity
Two uniform solid spheres having unequal radii are released from rest from the same height on a rough incline. the spheres roll without slipping
View SolutionFrom an inclined plane a sphere, a disc, a ring and a shell are rolled without slipping. The order of their reaching at the base will be
View SolutionThree bodies, a ring, a soild cylinder and a soild sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity ?
View SolutionA solid and a hollow sphere are released from the top of a sufficiently rough inclined plane. The solid sphere has same mass but its radius is half of the radius of hollow sphere. Both are performing pure rolling Which of the following statements is correct regarding their kinetic energy when they reach at the bottom of plane? (K = Kinetic energy)
View SolutionA cylinder is released from rest from the top of an incline of inclination θ and length 'L'. If the cylinder rolls without slipping. What will be its speed when it reaches the bottom?
View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) View Solution
View SolutionA ring, a solid cylinder, a hollow sphere and a solid sphere are released from rest on an inclined plane from same level. If there is no slipping then which one of these will reach the ground at last?
View Solution
