
A ring of mass and radius has a particle of mass attached to it at a point A. the ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring is released from rest when AB is horizontal. find the angular veloicity and the angular acceleration of the body when AB has turned through an angle .
Angular velocity from conservation of mechanical energy
decrease in gravitational PE
increase in rotational KE
or
angular acceleration
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
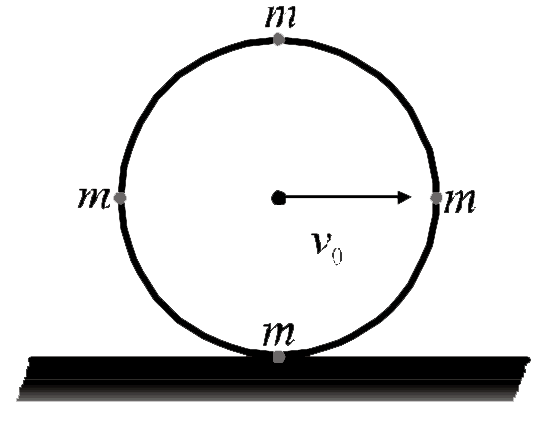
View SolutionA metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View Solution
Knowledge Check
There is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
AT=2π((Rg))BT=2π√(2Rg)CT=π√(2Rg)DT=2π√(3Rg)A ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
AVRB2VRCV2RD√2VRA ring of radius R is rotating about axis of ring such that angular velocity is given as = 5t. Find acceleration of a point P on rim after 5 sec
A5RB25RC√650RDNone of these
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA ring rotates without slipping on a horizontal smooth surface, the ratio of translational energy to the total energy of the ring is
View SolutionA ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
View Solution