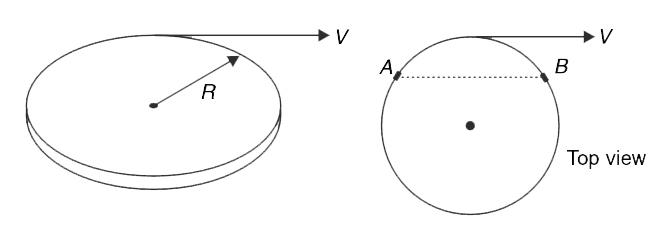
A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
Consider a small prt ACB of the ring that subtends an angle △θ aty te centre as shown in ure. Let the tension in te ring be T

The forces on this small part ACB are
a. tension T by the part of the ring left to A.
b. tension T by the part of the ring right to B,
c. weight (△m)g and
d.∥a∥lforceNbythetab≤<br>ThetensionatAactsalongthetan≥ntatAandtehtensionatBactsalongthetan≥ntatB.AsthesmallpartACBmoveds∈a∘≤ofradiusRataconstantspeedv,itsae≤rationistwoardsthecentre(alongCO)andhasamagnitude(/_\m)^2/R.<br>Resolv∈gtheforcesalongtheradiusCO<br>Tcos(90^0-/_\theta)/2+T cos (90^0-/_\theta)/2)=(v^2/R)<br>or 2Tsin(/_\m)(v^2/R)..........i<br>The≤n>hofthepartACBisR/_\theta.Asthe→talmassoftherig∩ismthemassofthepartACBwillbe/_\m=m(2piR)R/_\theta=(m/_\theta)/(2pi)<br>Pu∈g/_\m∈i.<br>2Tsin(/_\theta)/2=m/(2pi) /_\theta(v^2/R)<br>orT=(mv^2)/(2piR) (/_\theta/2)/(sin(/_\theta/2))<br>As /_\thetaisverysmall,(/_\theta/2)/(sin(/_\theta/2))~~1 and T=(mv^2)/(2piR^2).
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Short Answer
10 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 1
15 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
A chain of mass m and radius R placed on a smooth table is revolving with a speed v about a vertical axis coinciding with the symmetry axis of the chain. Find the tension in the chain.
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View Solution
Knowledge Check
A ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
AVRB2VRCV2RD√2VRA conducting rign of mass 100 gram and radius 0⋅5m is placed on a smooth horizontal plane. The ring carries a current of I=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in figure. The initial angular acceleration of the ring is
 A200πrad/s2B400πrad/s2C800πrad/s2D1200πrad/s2
A200πrad/s2B400πrad/s2C800πrad/s2D1200πrad/s2A small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 AvRB2vRCv2RD3vR
AvRB2vRCv2RD3vR
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA ring of mass M and radius R lies flat on a horizontal table. A light thread is wound around it and its free end is pulled with a constant velocity v.
(a) Two small segment A and B (see fig.) in the ring are rough and have a coefficient of friction μ with the table. Rest of the ring is smooth. Find the speed with which the ring moves.
(b) Find the speed of the ring if coefficient of friction is μ everywhere, for all points on the ring.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
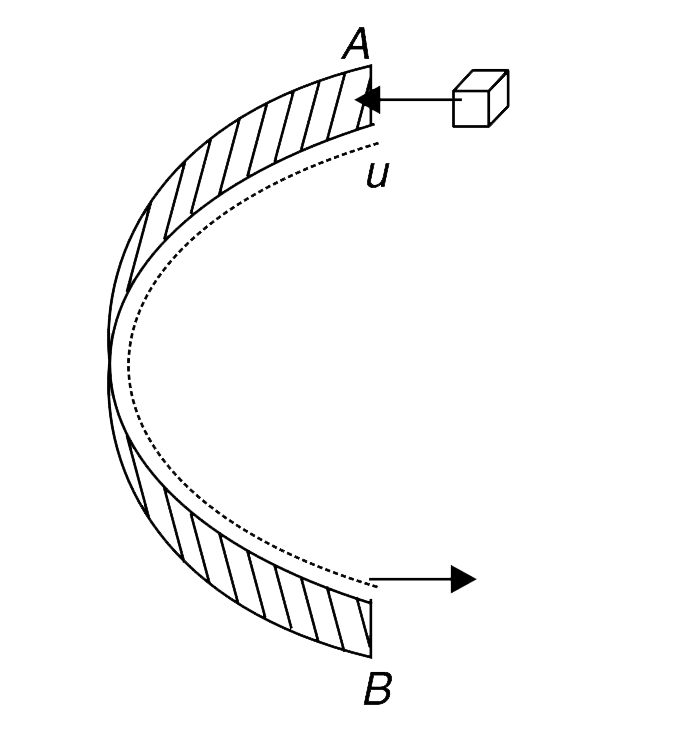
View SolutionA semicircular ring of radius R is fixed on a smooth horizontal table. A small block is projected with speed u so as to enter the ring at end A. Initial velocity of the block is along tangent to the ring at A and it moves on the table remaining in contact with the inner wall of the ring. The coefficient of friction between the block and the ring is μ.
(a) Find the time after which the block will exit the ring at B.
(b) With what speed will the block leave the ring at B.
View Solution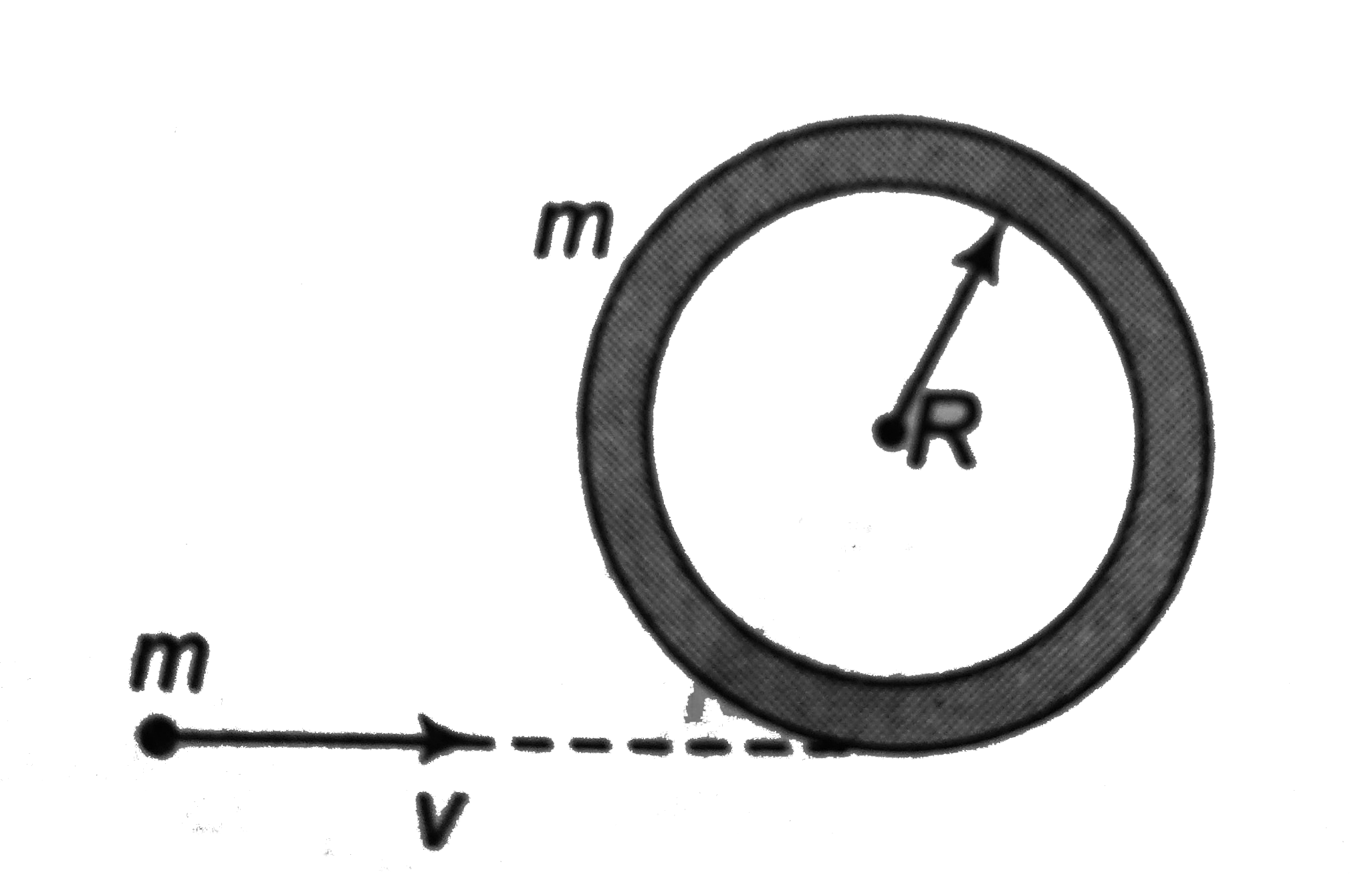
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View Solution