A ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
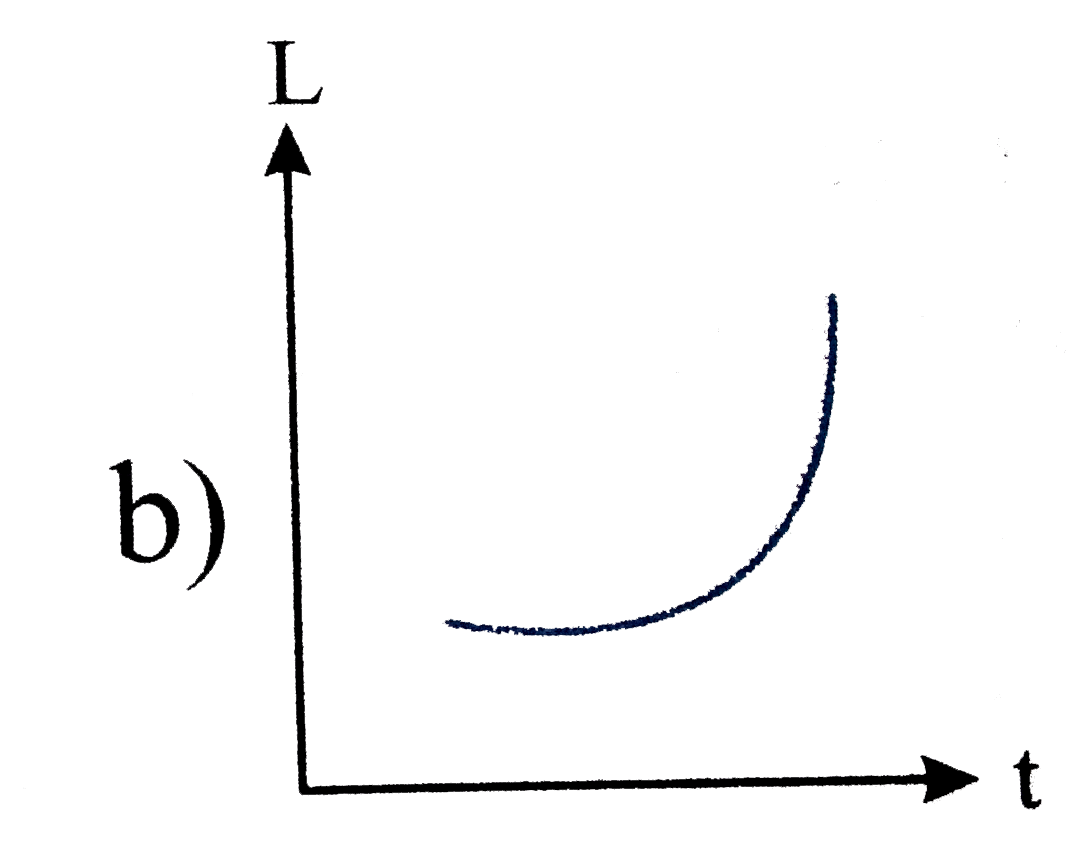


The correct Answer is:D
L=(mgsinθ)Rt, since , τ=ΔLΔt, so, L=τ(Δt)
The curve between L and time t will be a straight line.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


 View Solution
View SolutionA uniform sphere of mass m and radius R starts rolling without slipping down an inclined plane at an angle α to the horizontal. Find the time dependence of the angular momentum of the sphere relative to the point of contact at the initial moment. How will the obtained result change in the case of a perfectly smooth inclined plane?
View Solution
Knowledge Check
- Question 1 - Select One or More
A solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reduced - Question 2 - Select One
A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
ADecreases the rotational and translational motionBDissipates energy as heatCDecreases the rotational motionDConverts translational energy to rotational energy - Question 3 - Select One
A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
Adecreases the rotational and translational motionBdissipates energy as heatCdecreases the rotational motionDconverts translational energy to rotational energy
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
 View Solution
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :
 View Solution
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution

