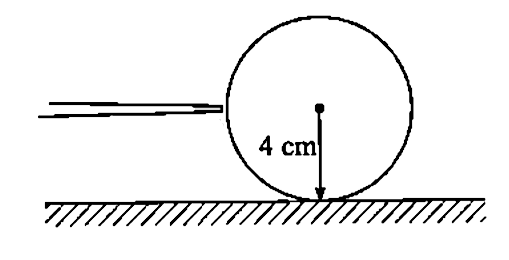
A ring of mass m connecting freely two identical thin hoops of mass M each starts sliding down. The hoops move apart over a rough horizontal surface. Determine the acceleration a of the ring at the initial instant if ∠AO1O2=α (Fig), neglecting the friction between the ring and the hoops.

Step by step video & image solution for A ring of mass m connecting freely two identical thin hoops of mass M each starts sliding down. The hoops move apart over a rough horizontal surface. Determine the acceleration a of the ring at the initial instant if /_AO_(1)O_(2) = alpha (Fig), neglecting the friction between the ring and the hoops. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
A ring of mass m having velocity v0 is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [μ is coefficient of friction between the ring and the plank.]
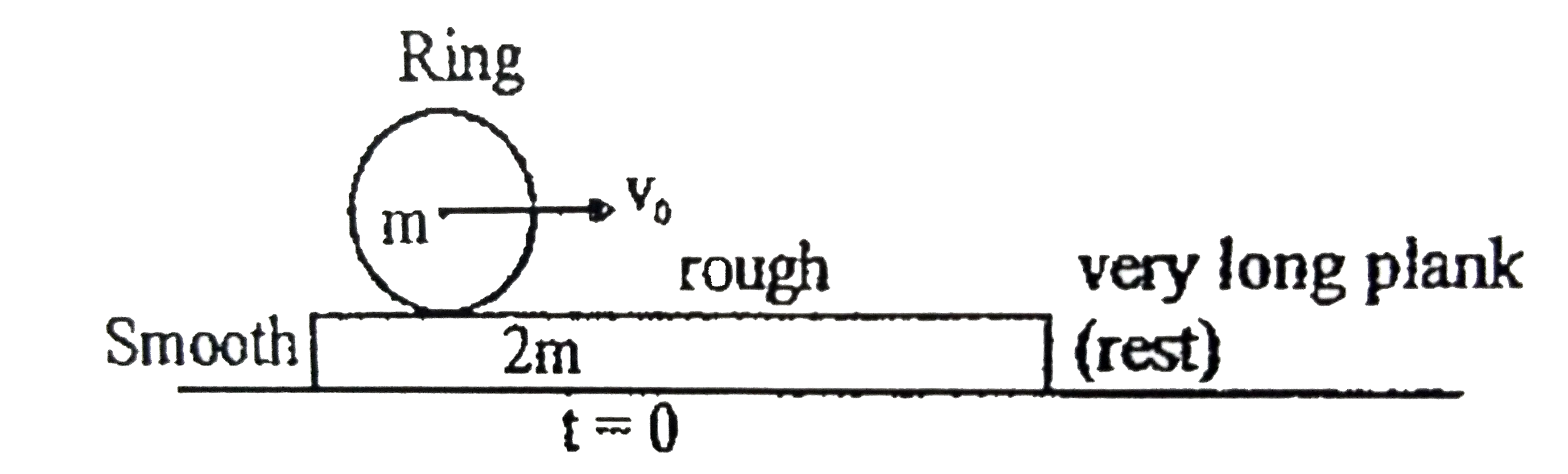 Av0μgBv04μgCv03μgD2v05μg
Av0μgBv04μgCv03μgD2v05μgCube of mass m kept on rough horizontal surface. Two insects each mass m. Moving in the cube with equal acceleration. a0 from D to E and H to F what is the frictional force by ground on the tube.
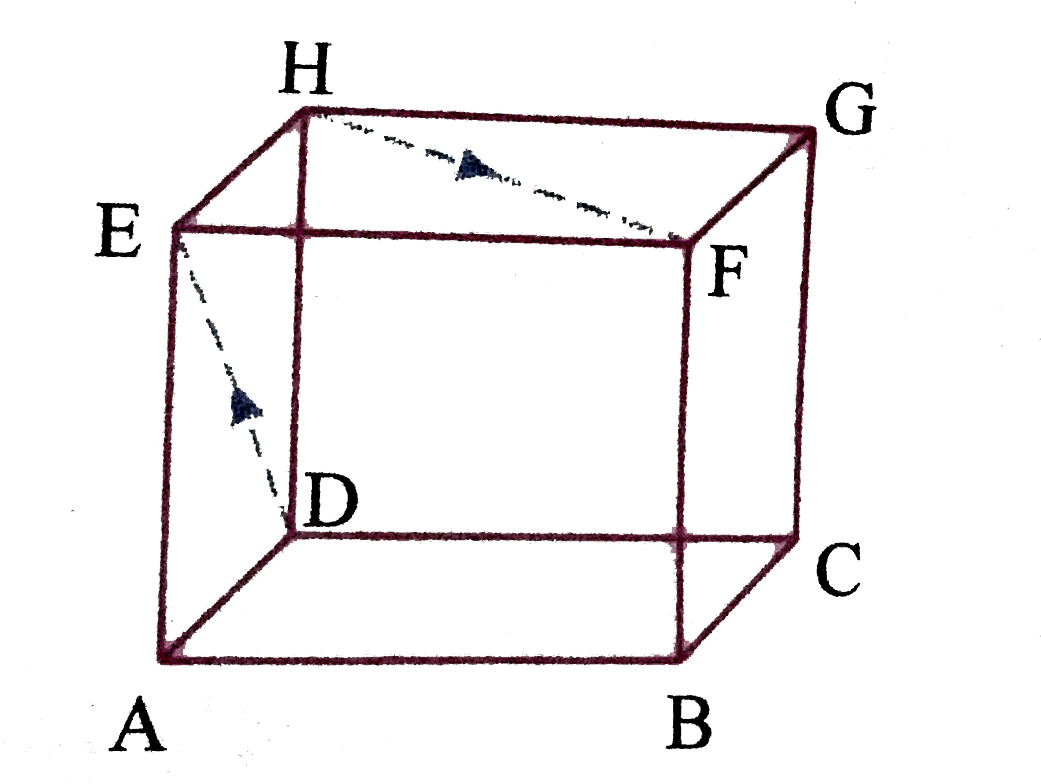 A(m+2m)a0B√5√2ma0C2ma0DMa0√2
A(m+2m)a0B√5√2ma0C2ma0DMa0√2An impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
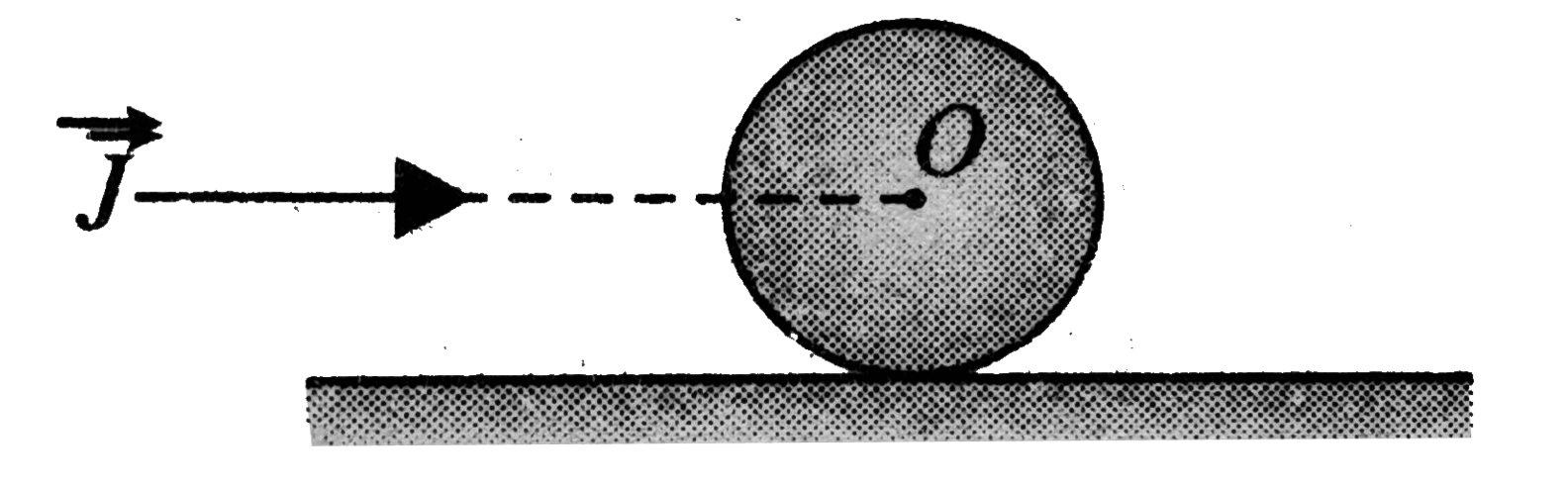 AJ/mBJ/2mCJ/4mDJ/3m
AJ/mBJ/2mCJ/4mDJ/3m
A ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is μ Then

View Solution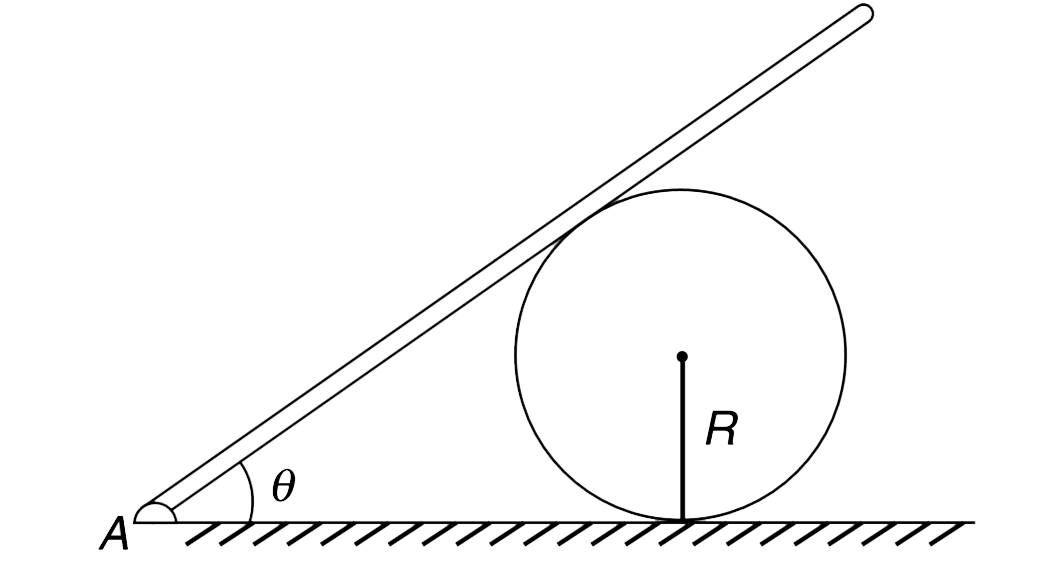
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.
View SolutionTwo identical beads each of mass 'm' can slide freely on a ring of mass M lying on smooth horizontal surface. The masses are brought to diametrically opposite positions and both are imparted with same tangential speed v in same direction. Find the kinetic energy of the ring when beads are about to collide.
View SolutionA uniform ring placed on a rough horizontal surface is given a sharp impulse as shown in the figure-5.130. As a consequence, it acquires a linear velocity of 2m/s. If coefficient of friction between the ring and the horizontal surface is 0.4 :
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
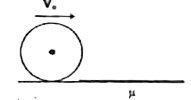
View Solution
