A ring (R), a disc (D), a solid sphere (S) and a hollow sphere with thin walls (H), all having the same mass but different radii, start together from rest at the top of inclined plane and roll down without slipping. Then
all of them will reach the bottom of the incline together
the body with the maximum radius will reach bottom first
they will reach the bottom in the order S,D,H and R
all of them will have the same kinetic energy at bottom of the incline
The correct Answer is:C, D
To solve the problem of determining which object reaches the bottom of the inclined plane first, we need to analyze the motion of each object (ring, disc, solid sphere, and hollow sphere) as they roll down the incline without slipping.
1. Understanding Rolling Motion:
- When an object rolls down an incline without slipping, its acceleration can be expressed as:
a=gsinθ1+IMR2
where g is the acceleration due to gravity, θ is the angle of the incline, I is the moment of inertia of the object, M is the mass, and R is the radius.
2. Moment of Inertia for Each Object:
- For the ring: IR=MR2
- For the disc: ID=12MR2
- For the solid sphere: IS=25MR2
- For the hollow sphere: IH=23MR2
3. Calculating Acceleration for Each Object:
- Ring:
aR=gsinθ1+1=gsinθ2
- Disc:
aD=gsinθ1+12=gsinθ32=2gsinθ3
- Solid Sphere:
aS=gsinθ1+25=gsinθ75=5gsinθ7
- Hollow Sphere:
aH=gsinθ1+23=gsinθ53=3gsinθ5
4. Comparing Accelerations:
- The accelerations calculated are:
- aR=gsinθ2
- aD=2gsinθ3
- aS=5gsinθ7
- aH=3gsinθ5
- To determine which object has the highest acceleration, we can compare the coefficients:
- aS>aH>aD>aR
5. Conclusion on Time Taken:
- Since acceleration is inversely related to the time taken to reach the bottom (higher acceleration means shorter time), we conclude:
- The solid sphere will take the least time, followed by the hollow sphere, then the disc, and finally the ring will take the longest time.
Final Order of Time Taken:
1. Solid Sphere (minimum time)
2. Hollow Sphere
3. Disc
4. Ring (maximum time)
- When an object rolls down an incline without slipping, its acceleration can be expressed as:
a=gsinθ1+IMR2
where g is the acceleration due to gravity, θ is the angle of the incline, I is the moment of inertia of the object, M is the mass, and R is the radius.
- For the ring: IR=MR2
- For the disc: ID=12MR2
- For the solid sphere: IS=25MR2
- For the hollow sphere: IH=23MR2
- Ring:
aR=gsinθ1+1=gsinθ2
- Disc:
aD=gsinθ1+12=gsinθ32=2gsinθ3
- Solid Sphere:
aS=gsinθ1+25=gsinθ75=5gsinθ7
- Hollow Sphere:
aH=gsinθ1+23=gsinθ53=3gsinθ5
- The accelerations calculated are:
- aR=gsinθ2
- aD=2gsinθ3
- aS=5gsinθ7
- aH=3gsinθ5
- aS>aH>aD>aR
- Since acceleration is inversely related to the time taken to reach the bottom (higher acceleration means shorter time), we conclude:
- The solid sphere will take the least time, followed by the hollow sphere, then the disc, and finally the ring will take the longest time.
1. Solid Sphere (minimum time)
2. Hollow Sphere
3. Disc
4. Ring (maximum time)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
A solid sphere rolls down two different inclined planes of the same height but of different inclinations
Athe speed and time of descend will be same.Bthe speed will be same but time of descend will be different.Cthe speed will be different but time are descend will be same.Dspeed and time of descend both are different..
A solid sphere rolls down two different inclined planes of the same height but of different inclinations
View SolutionA solid cylinder and a hollow cylinder, both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which one will reach the bottom first ?
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


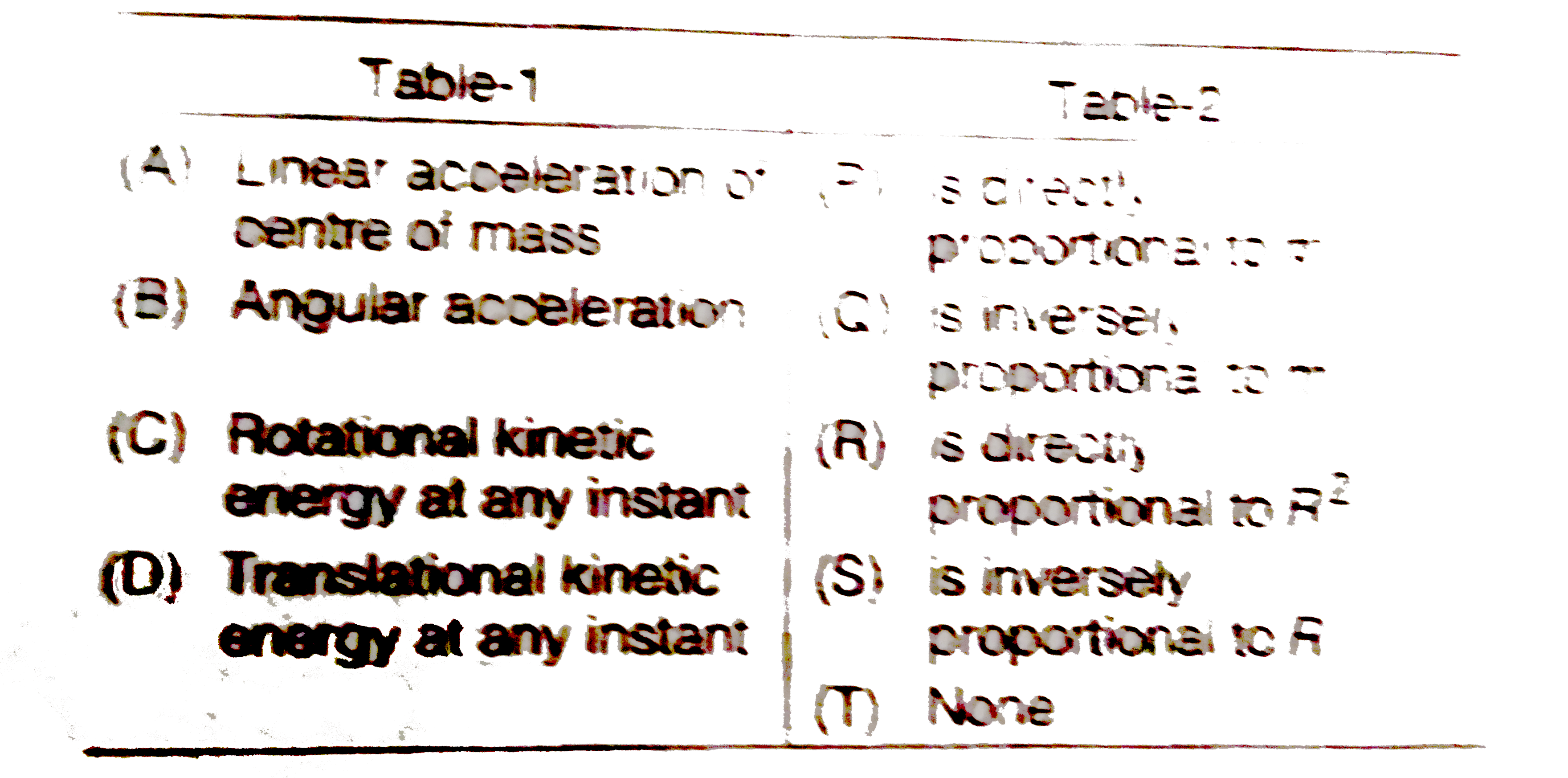
View SolutionTwo uniform solid spheres having unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping
View SolutionA solid cylinder and a solid sphere, both having the same mass and radius, are released from a rough inclined plane of inclination θ one by one. They roll on the inclined plane without slipping. The force of friction that acts
View SolutionA solid sphere and a solid cylinder having the same mass and radius, rolls down the same incline. The ratio of their acceleration will be
View SolutionA solid sphere, a hollow sphere and a disc, all having the same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The least time will be taken in reaching the bottom by
View Solution
