A rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle A of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a (not to scale) speed of v0/4. Find the following:
a. The ratio M/m.
b. The angular velocity of the rod about O.
c. The coefficient of restitution 'e' for the collision.
d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
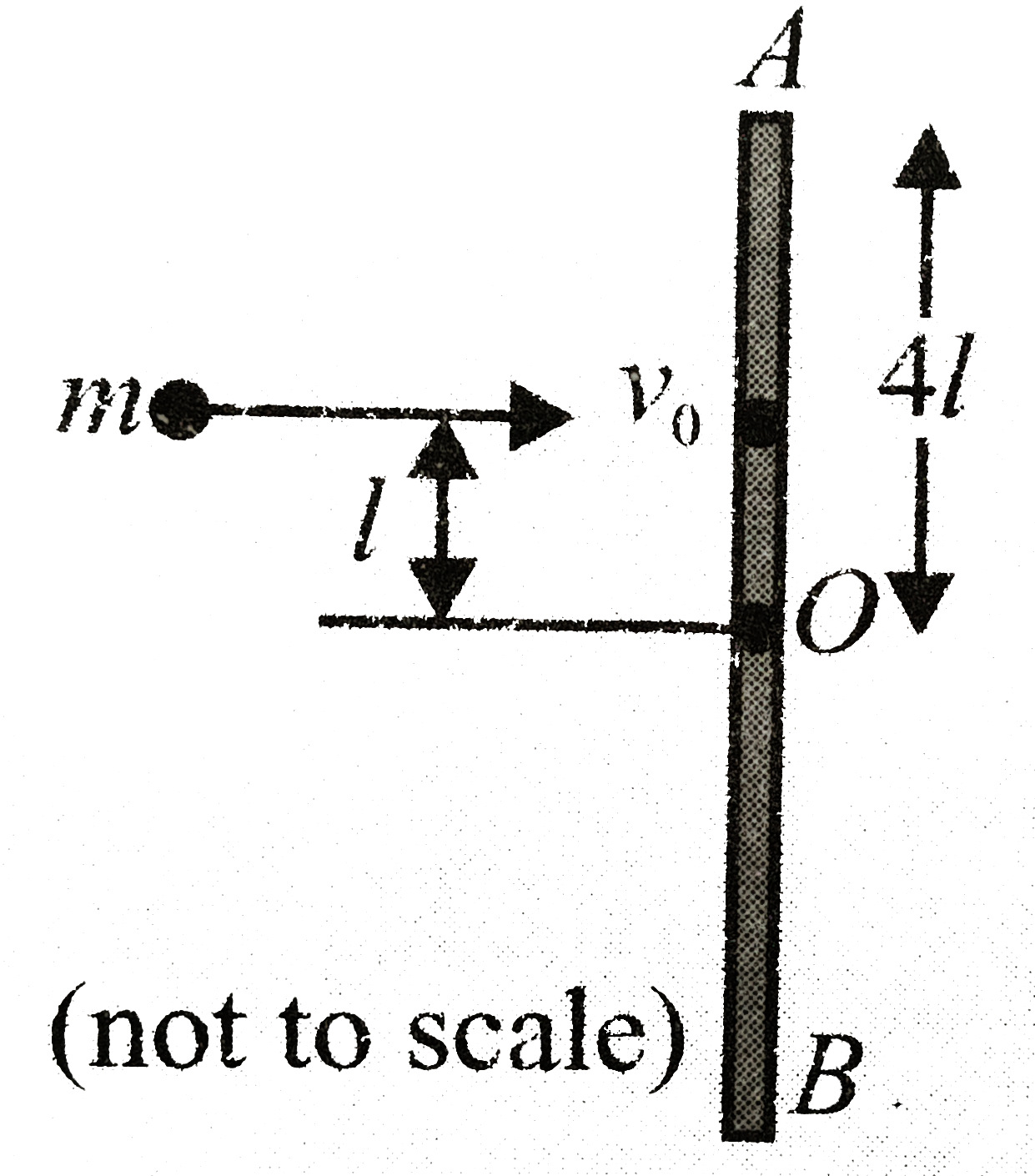
Mm=10
Mm=4
Mm=8
Mm=5
The correct Answer is:A
Conservation of linear momentum,
mv0=mv08−mv04,8m=m−2m
⇒10m=M
⇒Mm=10
conservation of angular momentum about point of collision.
0=M(8l)212ω−Mv08l
⇒ω=3v0128l
using coefficient of restitution equation
(v2−v1)=e(u1=u2)
[(v08+ωl)−(−v04)]=I[v0−0]
⇒e=51128
Velocity at end A
vA=v08+ω4l=28128v0
⇒vA=732v0
velocity at end B
vB=v08−ω4l=4128v0=132v0
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
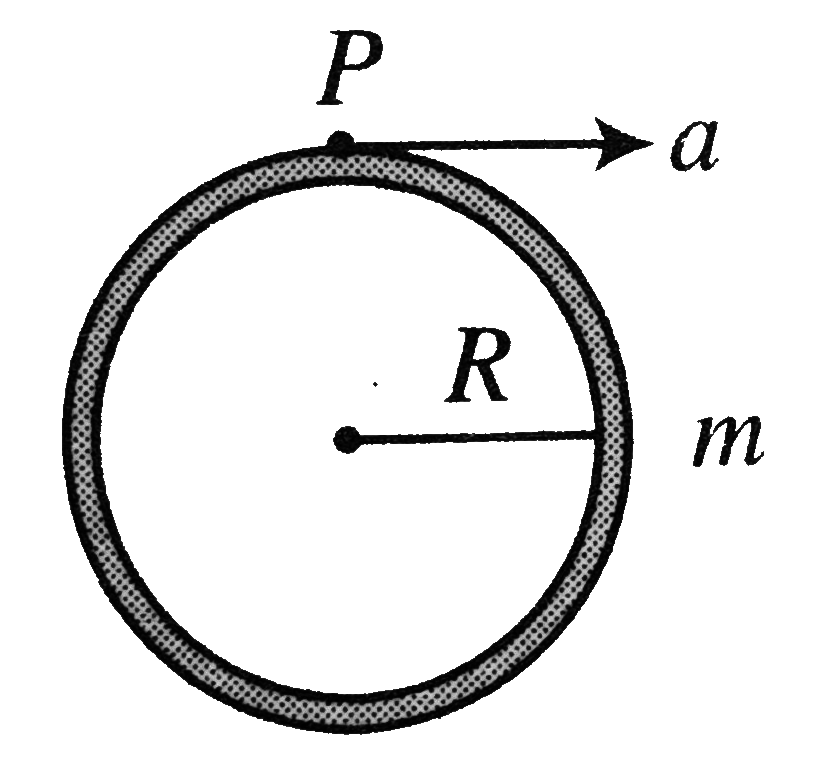
A smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
View SolutionA solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.

View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of A mass m and velocity v_(0) strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v_(0)//8 and the particle rebounds back with a (not to scale) speed of v_(0)//4 . Find the following: a. The ratio M//m . b. The angular velocity of the rod about O . c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, v_(A) and v_(B) respectively.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C of the system constituting 'the rod plus the particle'.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the angular momentum of the particle and of then about the centre of mass C before the collision.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v_(0) parallel to the initial position of the rod. (a) Calculate the acceleration of the centre of the rod immediately after the particle is projected. (b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
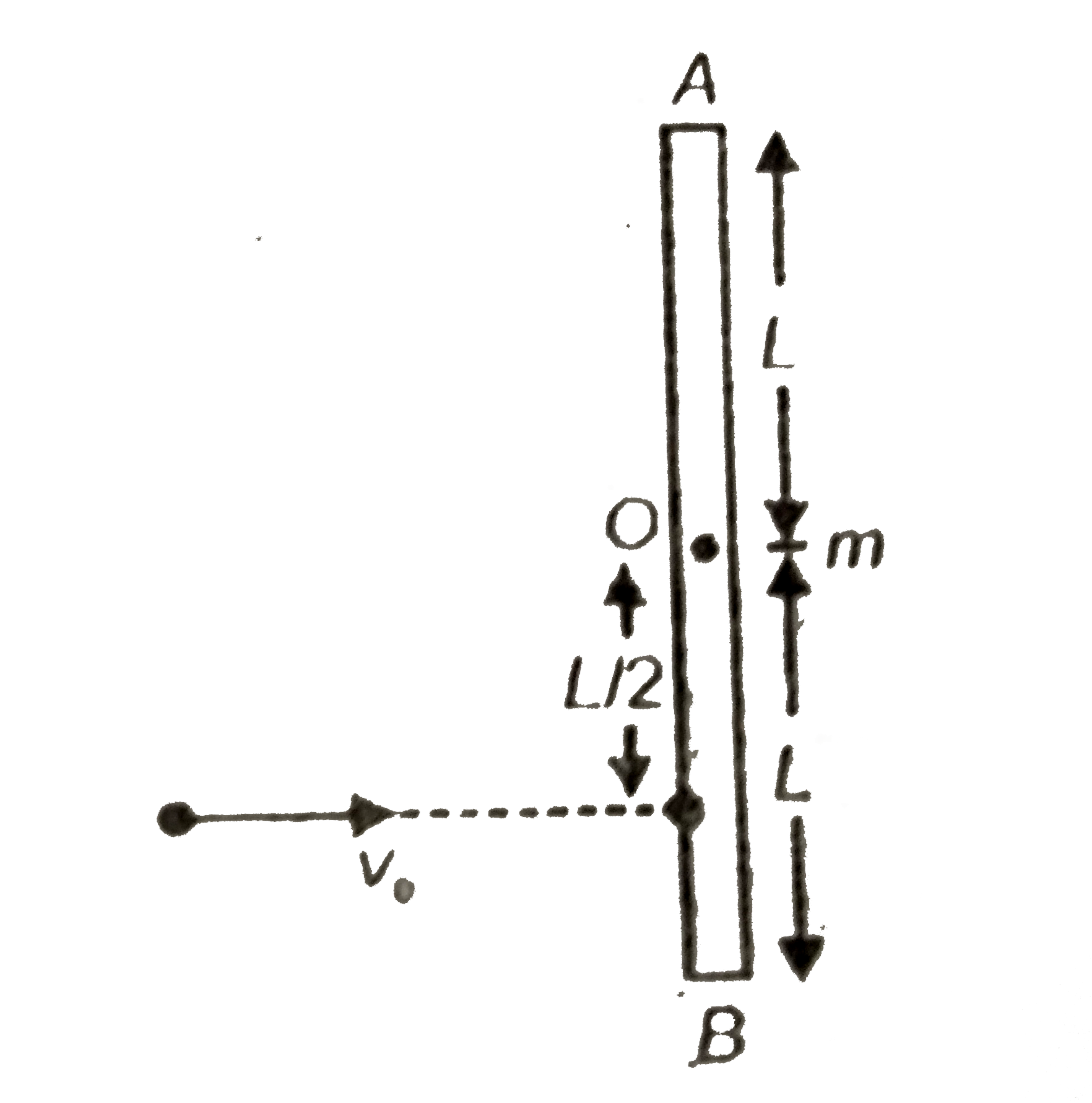
Angular velocity of rod just after collision is
View SolutionA uniform rod of length lambda lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out. The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View Solution
