A rod of 10 cm length is moving perpendicular to uniform magnetic field of intensity 5×10−4Wbm−2. If the acceleration of the rod is 5ms−2, then the rate of increase of induced emf is
25×10−4Vs−1
2.5×10−4Vs−1
20×10−4Vs−1
20×10−4Vs−1
The correct Answer is:B
To solve the problem step by step, we will follow the given parameters and apply the relevant formulas.
Step 1: Identify the given parameters
- Length of the rod (L) = 10 cm = 0.1 m (conversion from cm to m)
- Magnetic field intensity (B) = 5×10−4 Wb/m²
- Acceleration (a) = 5m/s2
Step 2: Write the formula for induced EMF
The formula for the motional EMF (E) induced in a rod moving through a magnetic field is given by:
E=B⋅V⋅L
where:
- E = induced EMF
- B = magnetic field intensity
- V = velocity of the rod
- L = length of the rod
Step 3: Relate velocity to acceleration
Since the rod is accelerating, we can express the velocity (V) in terms of acceleration (a) and time (t):
V=a⋅t
Step 4: Substitute the expression for velocity into the EMF formula
Substituting V=a⋅t into the EMF formula gives:
E=B⋅(a⋅t)⋅L
Step 5: Differentiate the EMF with respect to time to find the rate of increase of EMF
To find the rate of increase of induced EMF, we differentiate E with respect to time (t):
dEdt=B⋅a⋅L
Step 6: Substitute the known values into the differentiated formula
Now, we can substitute the values of B, a, and L:
- B=5×10−4Wb/m2
- a=5m/s2
- L=0.1m
Thus,
dEdt=(5×10−4)⋅(5)⋅(0.1)
Step 7: Calculate the result
Calculating the above expression:
dEdt=5×10−4⋅5⋅0.1=2.5×10−4V/s
Final Answer
The rate of increase of induced EMF is:
dEdt=2.5×10−4V/s
---
- Length of the rod (L) = 10 cm = 0.1 m (conversion from cm to m)
- Magnetic field intensity (B) = 5×10−4 Wb/m²
- Acceleration (a) = 5m/s2
The formula for the motional EMF (E) induced in a rod moving through a magnetic field is given by:
E=B⋅V⋅L
where:
- E = induced EMF
- B = magnetic field intensity
- V = velocity of the rod
- L = length of the rod
Since the rod is accelerating, we can express the velocity (V) in terms of acceleration (a) and time (t):
V=a⋅t
Substituting V=a⋅t into the EMF formula gives:
E=B⋅(a⋅t)⋅L
To find the rate of increase of induced EMF, we differentiate E with respect to time (t):
dEdt=B⋅a⋅L
Now, we can substitute the values of B, a, and L:
- B=5×10−4Wb/m2
- a=5m/s2
- L=0.1m
dEdt=(5×10−4)⋅(5)⋅(0.1)
Calculating the above expression:
dEdt=5×10−4⋅5⋅0.1=2.5×10−4V/s
The rate of increase of induced EMF is:
dEdt=2.5×10−4V/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A coil of area 500 cm2 having 1000 turns is put perpendicular to a magnetic field of intensity 4×10−5T. if it is rotated by 180∘ in 0.1 s, the induced emf produced is
View SolutionA rectangular coil of area 50cm2 and 100 turns is placed perpendicular to a magnetic field of 10−2Wb/m2. If the coil is withdrawn from the field in 40 ms, calculate the emf induced.
View SolutionA conductor of length 5 cm is moved paralllel to itself with a speed of 2m/s, perpendicular to a uniform magnetic field of 10−3Wb/m2. the induced emf generated is
View SolutionA conductor of length 5 cm is moved paralllel to itself with a speed of 2m/s, perpendicular to a uniform magnetic field of 10−3Wb/m2. the induced emf generated is
View SolutionA rectangular coil of dimensions 4 cm x 5 cm with number of turns 20 is placed with its plane perpendicular to a uniform magnetic field of 5 T. If it is moved with a speed of 2 m/s in the field parallel to its length, the e.m.f induced is
View SolutionRod PQ of length 2l is rotating about one end P in a uniform magnetic field B which is perpendicular to the plane of rotation of the rod . Point M is the mid- point of the rod. Find the induced emf between M and Q if the potential between P and Q is 100V.
 View Solution
View SolutionRod PQ of length 2l is rotating about one end P in a uniform magnetic field B which is perpendicular to the plane of rotation of the rod . Point M is the mid- point of the rod. Find the induced emf between M and Q if the potential between P and Q is 100V.
 View Solution
View SolutionA conducting rod of length / is rotating about point Pin a uniform transverse magnetic field B0 as shown in the figure. If angular speed of the rod is ω0 then the magnitude of induced emf across the ends of the rod will be (PA=2l3andPB=l3)
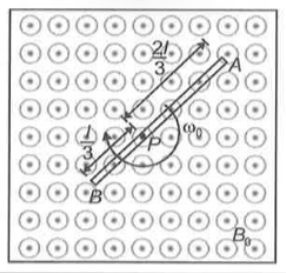 View Solution
View SolutionA wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the emf induced in the wire is 2 V, then the magnitude of the field in tesla is
View SolutionA rectangular coil of 300 turns has an average area of average area of 25cm×10cm the cooil rotates with a speed of 50cps in a uniform magnetic field of strength 4×10−2T about an axis perpendicular of the field. The peak value of the induced e.m.f. is (in volt)
View Solution

