A rod of length L and mass M is acted on by two unequal forces $F_{1}$ and $F_{2} (< F)$ as shown in the figure.

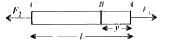
The tension in the rod at a distance y from the end A is given by

A

$F_{1} (1 - \frac{y}{L}) + F_{2} (\frac{y}{L})$

B

$F_{2} (1 - \frac{y}{L}) + F_{1} (\frac{Y}{L})$

C

$(F_{1} - F_{2}) \frac{y}{L}$

D

None of these

Text Solution

Verified by Experts

The correct Answer is:A

Net force on the rod $= F_{1} - F_{2}$
As mass of the rod is M , so acceleration of the rod is
$a = \frac{(F_{1} - F_{2})}{M}$
Now considering the motion of the rod [ whose mass is equal to $(m / L)$ y] then the equation of motion is
$F_{1} - T = \frac{M}{L} y \times a$
where T is the tension in the rod at B .
$or F_{1} - T = \frac{M}{L} y \times (\frac{F_{1} - F_{2}}{M})$
$or T = F_{1} (1 - \frac{y}{L}) + F_{2} (\frac{y}{L})$
second method : to calculate tension at B we can also consider the motion of the other of the rod i.e., BC . then the equation of motion will be
$T - F_{2} = \frac{M}{L} (l - y) \times a$
$or T = F_{2} \frac{M}{L} (L - y) \times \frac{(F_{1} - F_{2})}{M}$ ( using (i))
$or T = F_{1} (1 - \frac{y}{L}) + F_{2} (\frac{y}{L})$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZero
BF
C $\frac{F (L - y)}{L}$
D $\frac{F (l - y)}{M}$
Question 2 - Select One or More
Two forces $F_{1} and F_{2}$ are acting on a rod abc as shown in figure.

Aif $F_{1} = F_{2}$ then $τ_{a} = τ_{b} = τ_{c}$ ( for both forces)
Bif $F_{1} = F_{2}$ then $τ_{a} = τ_{c} \neq τ_{b}$ ( for both forces)
Cif $F_{1} \neq F_{2}$ then $τ_{a} \neq τ_{b} \neq τ_{c}$ ( for both forces)
Dif $F_{1} \neq F_{2}$ then $τ_{a} = τ_{c} \neq τ_{b}$ ( for both forces)
Question 3 - Select One
A rod length $L$ and mass $M$ is placed along the $x$ -axis with one end at the origin, as shown in the figure above. The rod has linear mass density $λ = \frac{2 M}{L^{2}} x,$ where $x$ is the distance from the origin. Which of the following gives the $x$ -coordinate of the rod's center of mass?
A $\frac{2}{3} L$
B $\frac{1}{4} L$
C $\frac{1}{3} L$
D $\frac{1}{2} L$

MTG GUIDE-LAWS OF MOTION-NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) ( NEWTON.S LAWS OF MOTION)

Home
Ask Doubt
Profile