A homogeneous rod of length L is acted upon by two forces F1andF2 applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F1 is applied?
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the System
We have a homogeneous rod of length L with two forces F1 and F2 applied at its ends in opposite directions. We need to find the force F at a cross-section located at a distance l from the end where F1 is applied.
Step 2: Identify the Net Force
The net force acting on the rod can be expressed as:
Fnet=F2−F1
This net force will cause the entire rod to accelerate.
Step 3: Relate Net Force to Acceleration
Using Newton's second law, we can relate the net force to the mass and acceleration of the rod:
Fnet=m⋅a
Here, the mass m of the rod can be expressed in terms of its density λ and length L:
m=λ⋅L
Thus, we can write:
F2−F1=λ⋅L⋅a(1)
Step 4: Analyze the Small Portion of the Rod
Now, consider a small portion of the rod with length l from the end where F1 is applied. The forces acting on this small portion are F (the force at the cross-section) and F1.
Step 5: Apply Newton's Second Law to the Small Portion
For this small portion, we can write:
F−F1=λ⋅l⋅a0(2)
where a0 is the acceleration of the small portion.
Step 6: Relate Accelerations
Since the entire rod is accelerating uniformly, the acceleration a0 of the small portion can be expressed in terms of the total acceleration a:
a0=a⋅lL
Step 7: Substitute Acceleration in Equation (2)
Substituting a0 into equation (2):
F−F1=λ⋅l⋅(a⋅lL)
Step 8: Substitute a from Equation (1)
From equation (1), we can express a:
a=F2−F1λ⋅L
Substituting this into the previous equation gives:
F−F1=λ⋅l⋅(F2−F1λ⋅L⋅lL)
Step 9: Simplify the Equation
Canceling λ from both sides:
F−F1=lL⋅(F2−F1)⋅lL
Thus, we can rearrange to find F:
F=F1+lL⋅(F2−F1)
Final Answer
The force F at the cross-section at a distance l from the end where F1 is applied is:
F=F1+lL⋅(F2−F1)
We have a homogeneous rod of length L with two forces F1 and F2 applied at its ends in opposite directions. We need to find the force F at a cross-section located at a distance l from the end where F1 is applied.
The net force acting on the rod can be expressed as:
Fnet=F2−F1
This net force will cause the entire rod to accelerate.
Using Newton's second law, we can relate the net force to the mass and acceleration of the rod:
Fnet=m⋅a
Here, the mass m of the rod can be expressed in terms of its density λ and length L:
m=λ⋅L
Thus, we can write:
F2−F1=λ⋅L⋅a(1)
Now, consider a small portion of the rod with length l from the end where F1 is applied. The forces acting on this small portion are F (the force at the cross-section) and F1.
For this small portion, we can write:
F−F1=λ⋅l⋅a0(2)
where a0 is the acceleration of the small portion.
Since the entire rod is accelerating uniformly, the acceleration a0 of the small portion can be expressed in terms of the total acceleration a:
a0=a⋅lL
Substituting a0 into equation (2):
F−F1=λ⋅l⋅(a⋅lL)
From equation (1), we can express a:
a=F2−F1λ⋅L
Substituting this into the previous equation gives:
F−F1=λ⋅l⋅(F2−F1λ⋅L⋅lL)
Canceling λ from both sides:
F−F1=lL⋅(F2−F1)⋅lL
Thus, we can rearrange to find F:
F=F1+lL⋅(F2−F1)
The force F at the cross-section at a distance l from the end where F1 is applied is:
F=F1+lL⋅(F2−F1)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.3
19 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Knowledge Check
A rope of length L is pulled by a constant force F. What is the tension in the rope at a distance x from the end where the force is applied ?
AFL/xBF(L−x)/LCFL/(L−x)DFx/(L−x)A rigid rod of length 2L is acted upon by some forces. All forces labelled F have the same magnitude. Which cases have a non-zero net torque acting on the rod about its centre ?
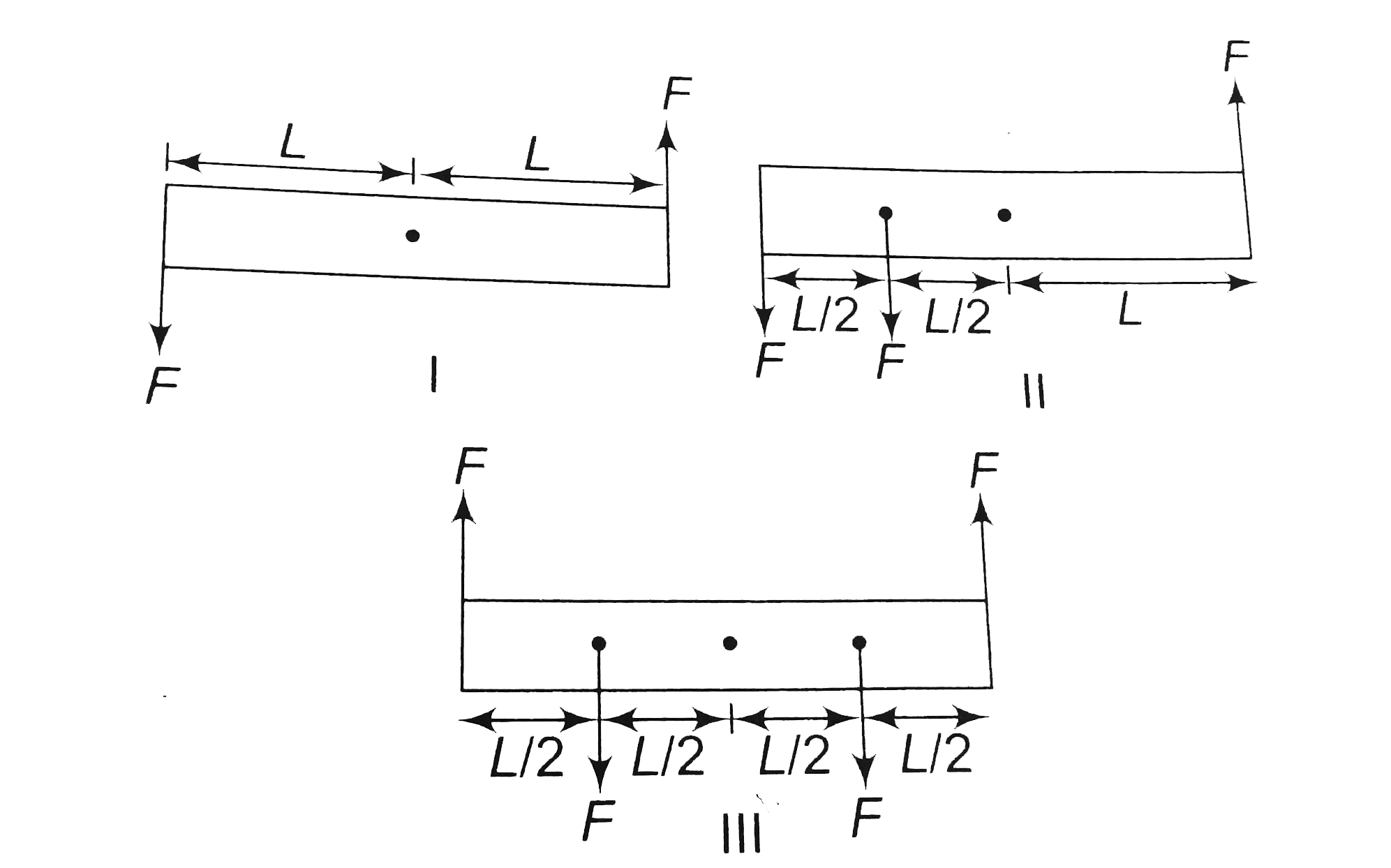 .AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
.AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
A uniform rod of length l is applied upon by two forces at its either end as shown. Surface is smooth. Which of the following option is correct ?
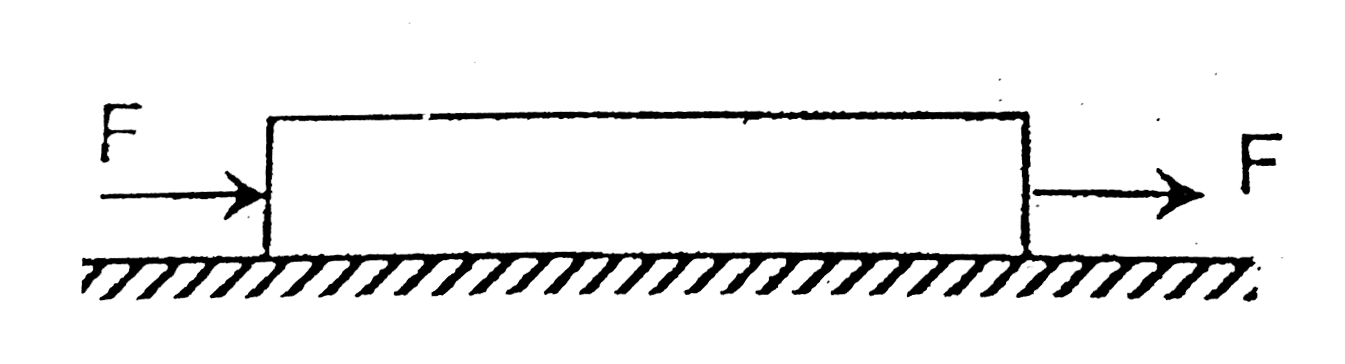
View SolutionA rod of length L and mass M is acted on by two unequal force F1andF2(<F1) as shown in the following figure.

The tension in the rod at a distance y from the end a is given by
View SolutionA rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Expression Tx of tension at a point at distance x from the end A is
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA uniform rope of length L, resting on a frictionless horizontal table is pulled at one end by a force F. What is the tension in the rope at a distance x form the end where the force is applied?
View Solution


