A rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
The correct Answer is:A, B, D
Restoring torque
τ=−(klθ)l−(kl2θ)l2=−54kl2θ
Now, (ml23)α=−(54kl2)θ
f=12π√∣∣∣αθ∣∣∣=12π√15k4m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
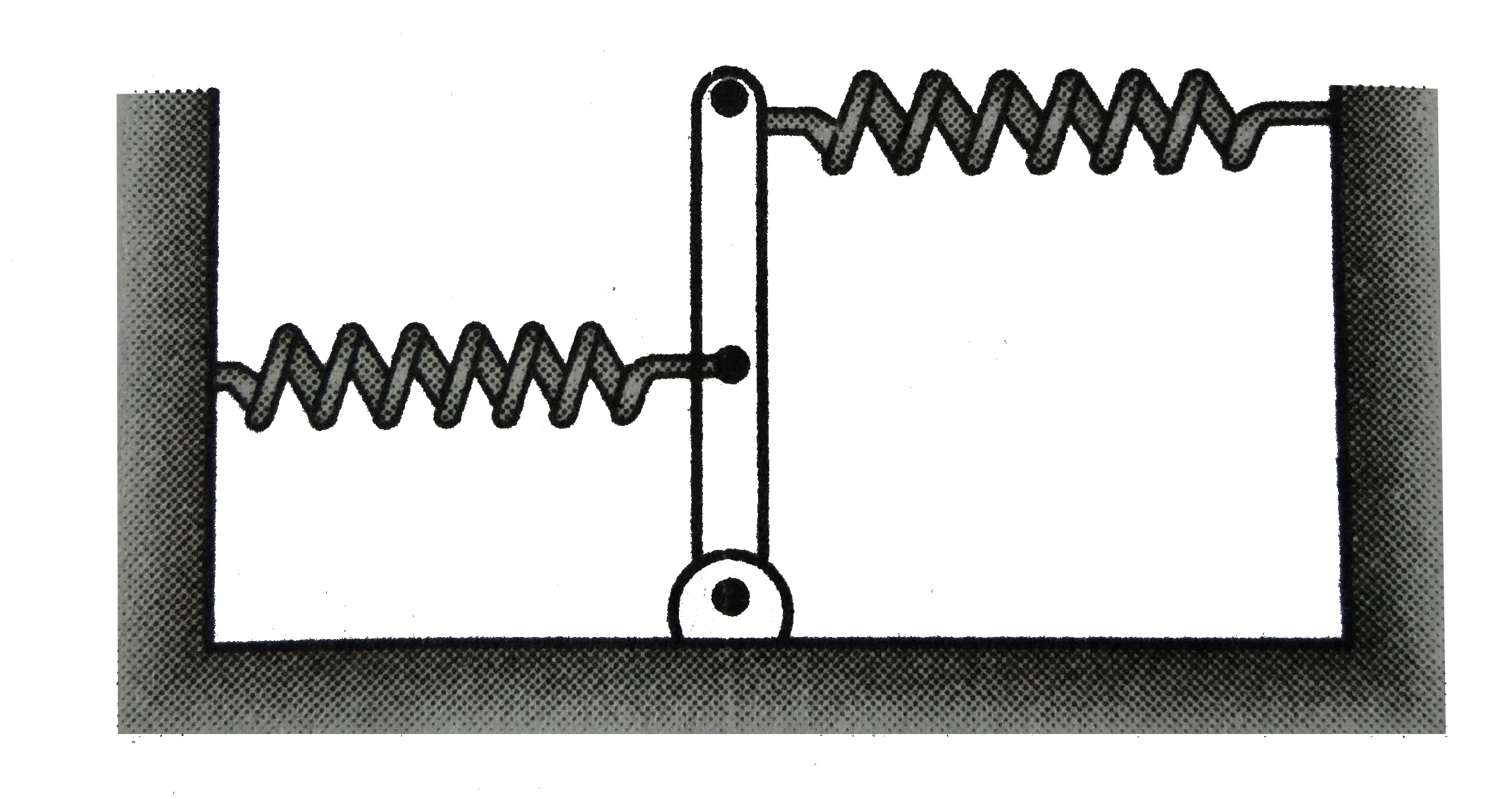
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
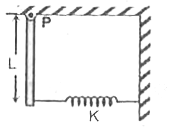
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View Solution
Knowledge Check
Two spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
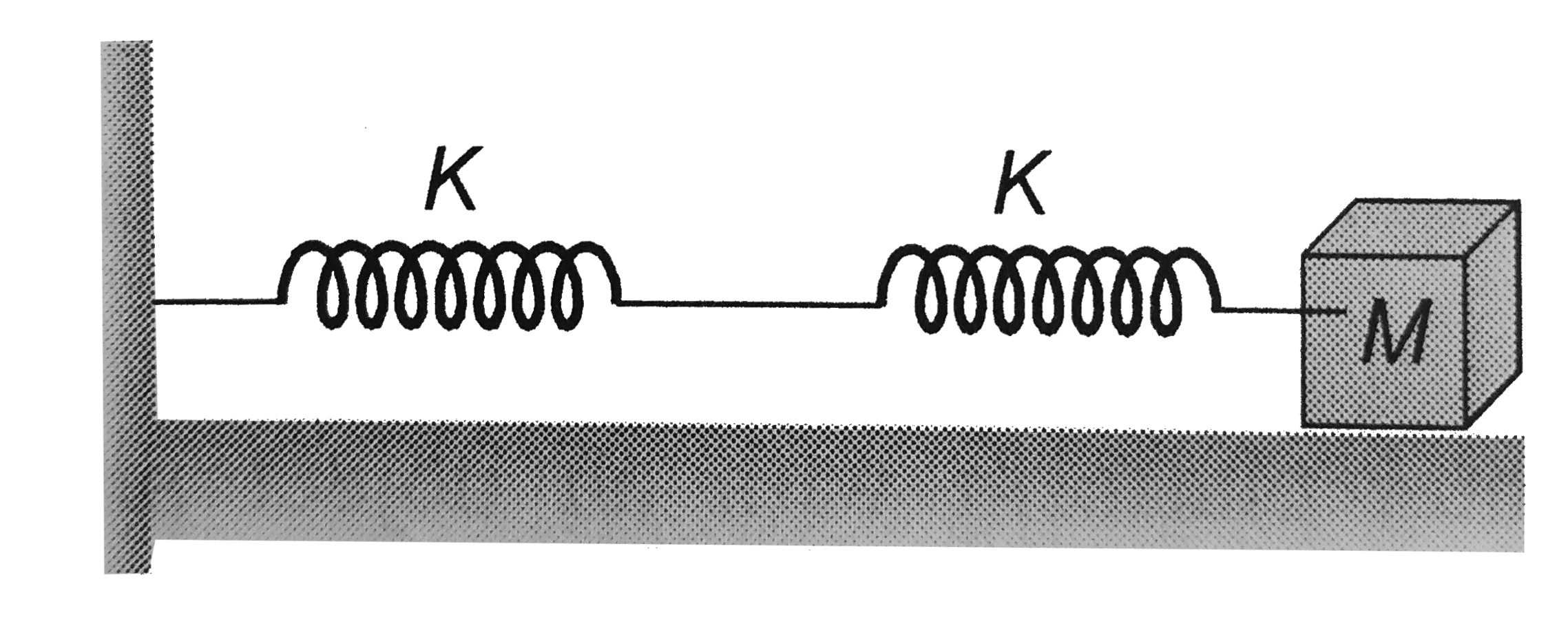 A12π√k2MB12π√kMC12π√2kMD12π√Mk
A12π√k2MB12π√kMC12π√2kMD12π√MkA uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 A12π√2kMB12π√kMC12π√6kMD12π√24kM
A12π√2kMB12π√kMC12π√6kMD12π√24kMTwo springs are joined and connected to mass m as shown. If the springs separately have force constants K1 and K2 , then frequency of oscillation of mass m is
 A12π√K1K2(K1+K2)mB2π√(K1+K2)mK1K2C2π√K1K2mD12π√mK1+K2
A12π√K1K2(K1+K2)mB2π√(K1+K2)mK1K2C2π√K1K2mD12π√mK1+K2
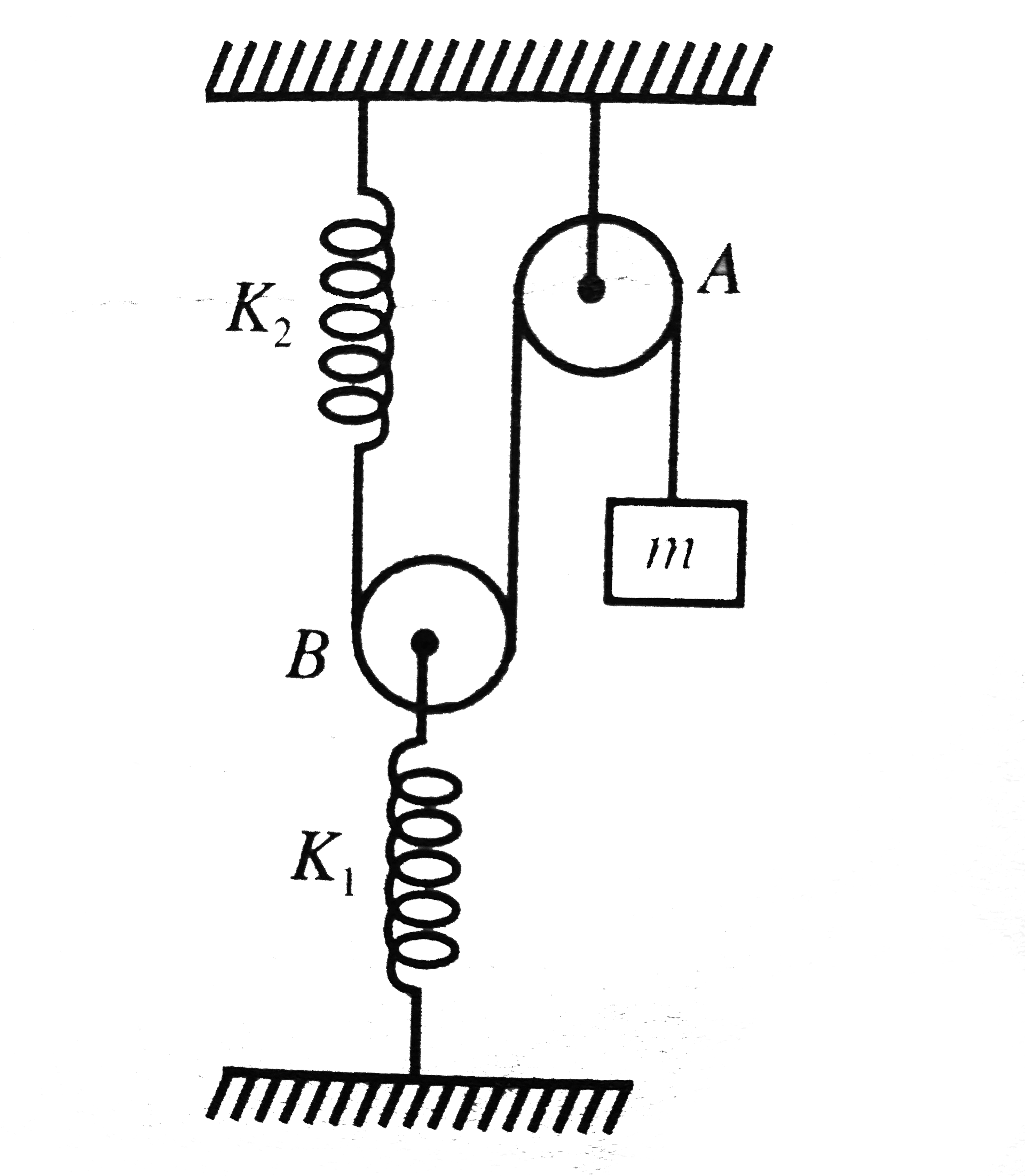
A light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
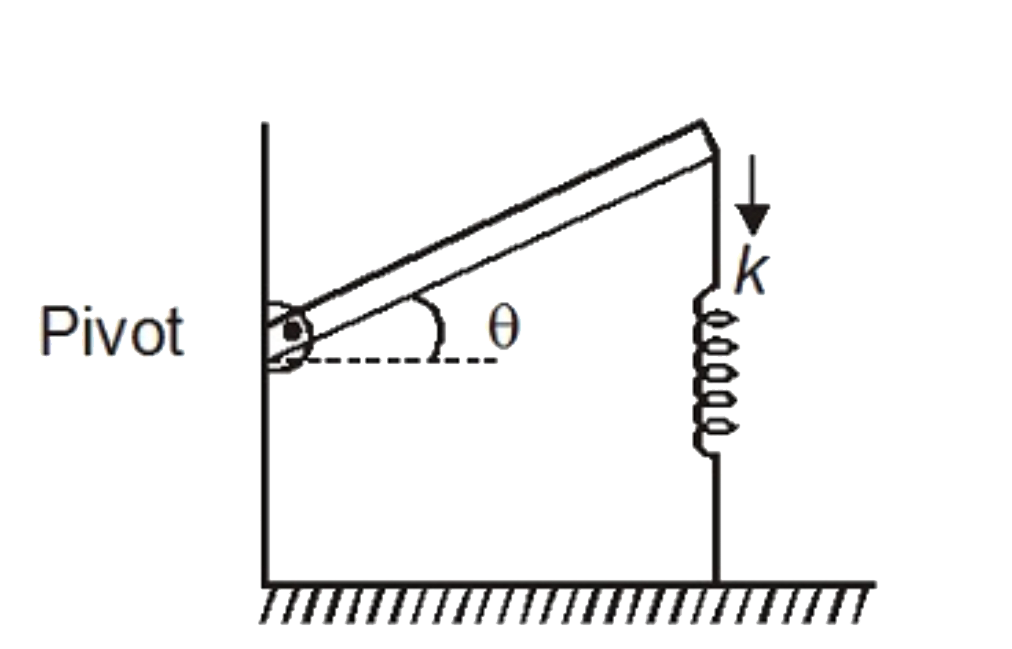
View Solution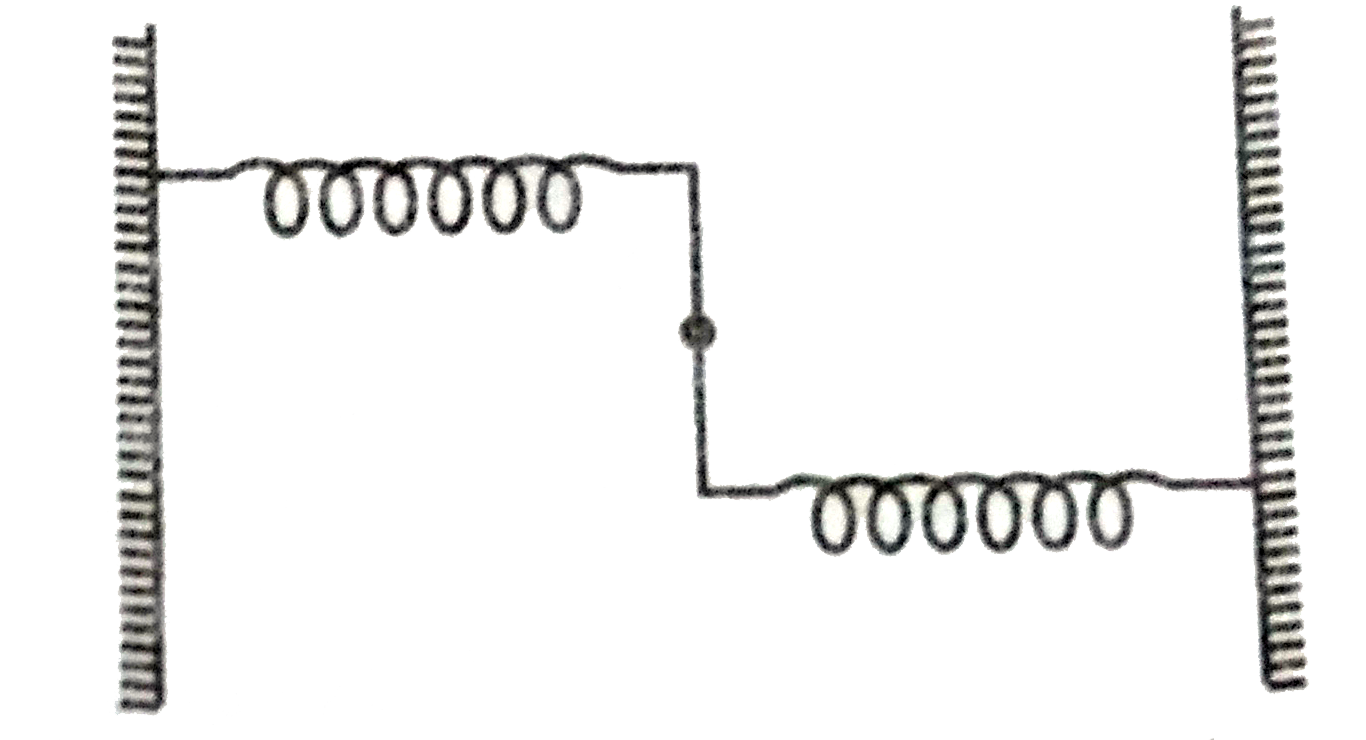
A uniform rod of length l and mass M is pivoted at the centre. Its two ends are attached to two ends are attached to two springs of equal spring constant k. the springs are fixed to rigid support as shown in figure and the rod is free to oscillate in the horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscillation is
View SolutionIn the figure all spring are identical having spring constant k and mass m each .The block hav also mass m .The frequency of oscillation of the block is
View SolutionThe arrangement shown of a uniform rod of length l and mass m, pivoted at the centre and its two ends attached to two springs of spring constant K1 and K2 . The other end of springs are fixed to two rigid supports the rod which is free to rotate in the horizontal plane , is pushed by a small angle in one direction and released . Teh frequency of oscillation of the rod is
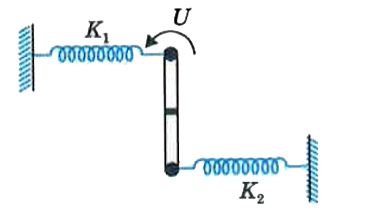
View Solution
