A rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
2ms−1
1ms−1
4ms−1
1.5ms−1
The correct Answer is:D
To solve the problem, we need to find the velocity of the end of the rod in contact with the surface when the rod makes an angle of 37∘ with the horizontal and the velocity of the center of mass (COM) is 2m/s.
1. Understand the Geometry of the Rod:
- The rod is making an angle of 37∘ with the horizontal.
- The length of the rod is L.
- The center of mass (COM) of the rod is located at a distance of L/2 from either end.
2. Identify the Velocities:
- The velocity of the center of mass (COM) is given as VCOM=2m/s downward.
- Let the angular velocity of the rod be ω.
3. Determine the Velocity Components:
- The velocity of the point P (the end of the rod in contact with the surface) has two components:
- A vertical component due to the rotation of the rod.
- A horizontal component due to the motion of the center of mass.
4. Vertical Component of Velocity:
- The vertical component of the velocity of point P can be expressed as:
VP,vertical=ωL2cos(37∘)−VCOM
- Since the rod is in contact with the surface, this vertical component should equal zero:
ωL2cos(37∘)−2=0
- Rearranging gives:
ωL2cos(37∘)=2
5. Horizontal Component of Velocity:
- The horizontal component of the velocity of point P is given by:
VP,horizontal=ωL2sin(37∘)
6. Relate the Two Components:
- From the vertical velocity equation, we can express ω:
ω=4Lcos(37∘)
- Substitute this into the horizontal component:
VP,horizontal=(4Lcos(37∘))L2sin(37∘)=2sin(37∘)cos(37∘)=2tan(37∘)
7. Calculate the Velocity of Point P:
- Since tan(37∘)=34:
VP,horizontal=2⋅34=32m/s=1.5m/s
Final Answer:
The velocity of the end of the rod in contact with the surface is 1.5m/s.
- The rod is making an angle of 37∘ with the horizontal.
- The length of the rod is L.
- The center of mass (COM) of the rod is located at a distance of L/2 from either end.
- The velocity of the center of mass (COM) is given as VCOM=2m/s downward.
- Let the angular velocity of the rod be ω.
- The velocity of the point P (the end of the rod in contact with the surface) has two components:
- A vertical component due to the rotation of the rod.
- A horizontal component due to the motion of the center of mass.
- The vertical component of the velocity of point P can be expressed as:
VP,vertical=ωL2cos(37∘)−VCOM
- Since the rod is in contact with the surface, this vertical component should equal zero:
ωL2cos(37∘)−2=0
- Rearranging gives:
ωL2cos(37∘)=2
- The horizontal component of the velocity of point P is given by:
VP,horizontal=ωL2sin(37∘)
- From the vertical velocity equation, we can express ω:
ω=4Lcos(37∘)
- Substitute this into the horizontal component:
VP,horizontal=(4Lcos(37∘))L2sin(37∘)=2sin(37∘)cos(37∘)=2tan(37∘)
- Since tan(37∘)=34:
VP,horizontal=2⋅34=32m/s=1.5m/s
The velocity of the end of the rod in contact with the surface is 1.5m/s.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
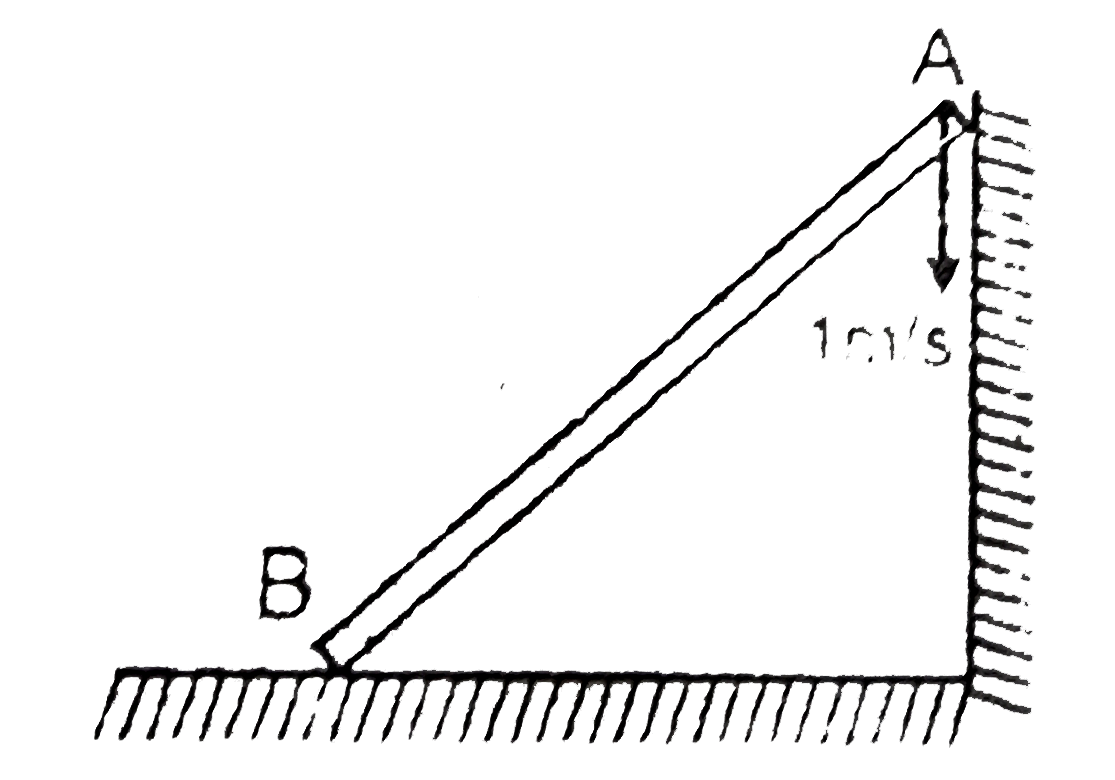
A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
View SolutionA uniform rod of length l is kept vertically on a rough horizontal surface at x = 0 . It is rotated slightly and released . When the rod finally falls on the horizontal surface , the lower end will remain at

View SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The velocity of centre of mass of rod is :
View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

View SolutionA rod of mass m is released on smooth horizontal surface making angle θ with horizontal. Then which of the following statement is correct ?
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View Solution
