A rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

The fall in postion of the CM of the rod, h=12(1−cosθ)
In the process, decrease in E is equal to increase in rotational
KE of the rod, so mgh=12Iω2
or mg12(3gl(1−cosθ))
The velocity of the CM of the rod VCM=ωr is
√3gl(1−cosθ)×l2=√3gl(1−cosθ)4
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
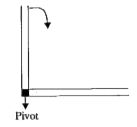
A half metre scale is pivoted about a horizontal fiictionless pin through one end as shown in Fig. The scale is released from rest in a vertical position. At the instant when the scale is horizontal what is (i) its angular speed and (ii) the magnitude of the angular acceleration.(Given length of rod =1/2 m)
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA slender rod of mass m and length L is pivoted about a horizontal axis through one end and released from rest at an angle of 30∘ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is

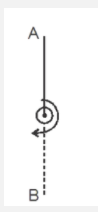
View SolutionA uniform rod is rotating about a horizontal axis as shown. The rod is hinged at one of the ends. The rod is released from a vertical position by slightly pushing it. As the rod moves from A to B
View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View Solution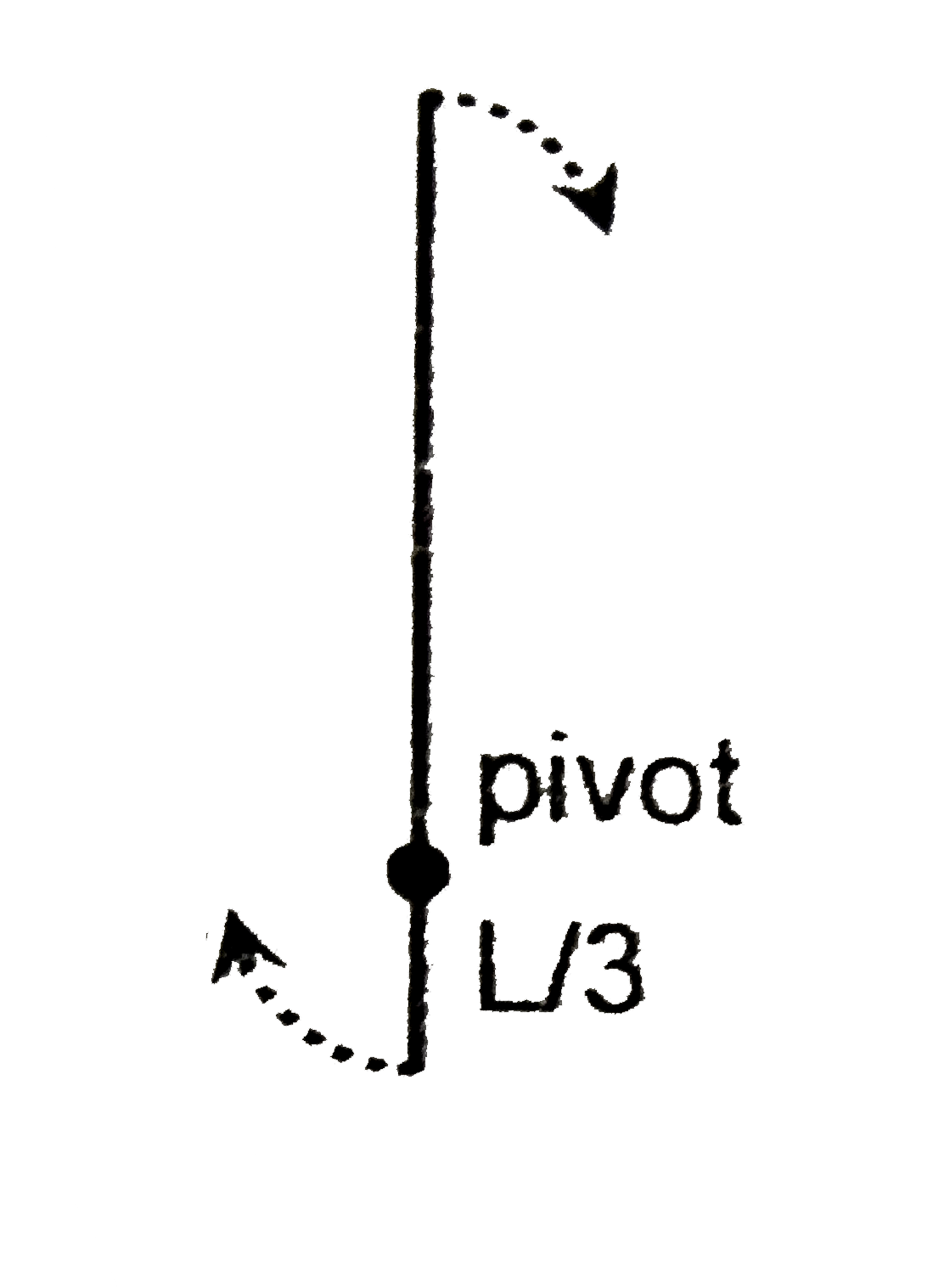
A uniform rod of mass M and length L is free to rotate about a frictionless pivot located L/3 from one end. The rod is released from rest incrementally away from being perfectly vertical, resulting in the rod rotating clockwise about the pivot. when the rod is horzontal what is the magnitude of the tangential acceleration of its center of mass?
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
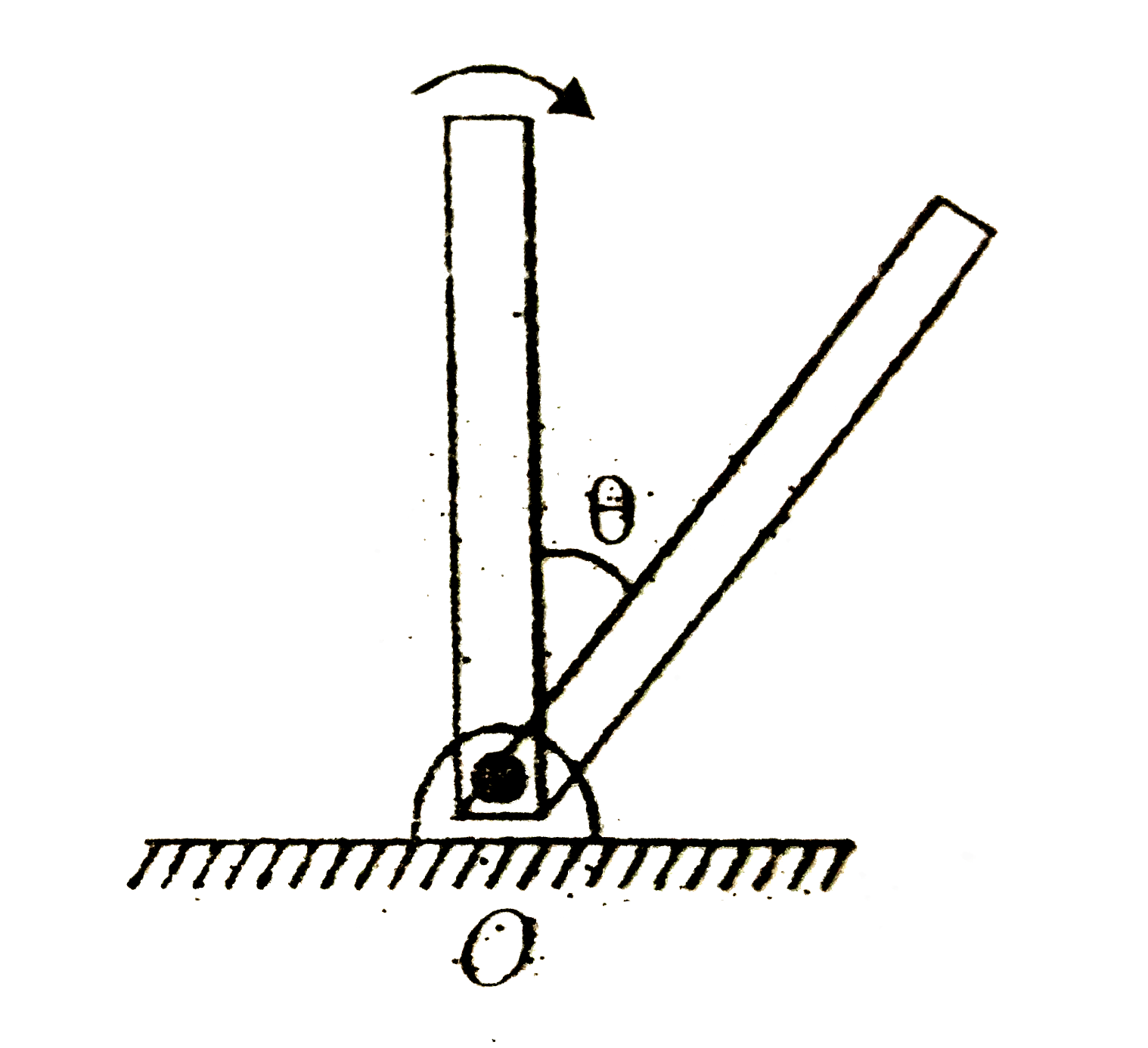
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
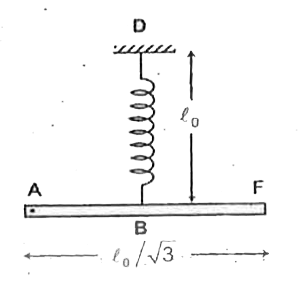
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View Solution
