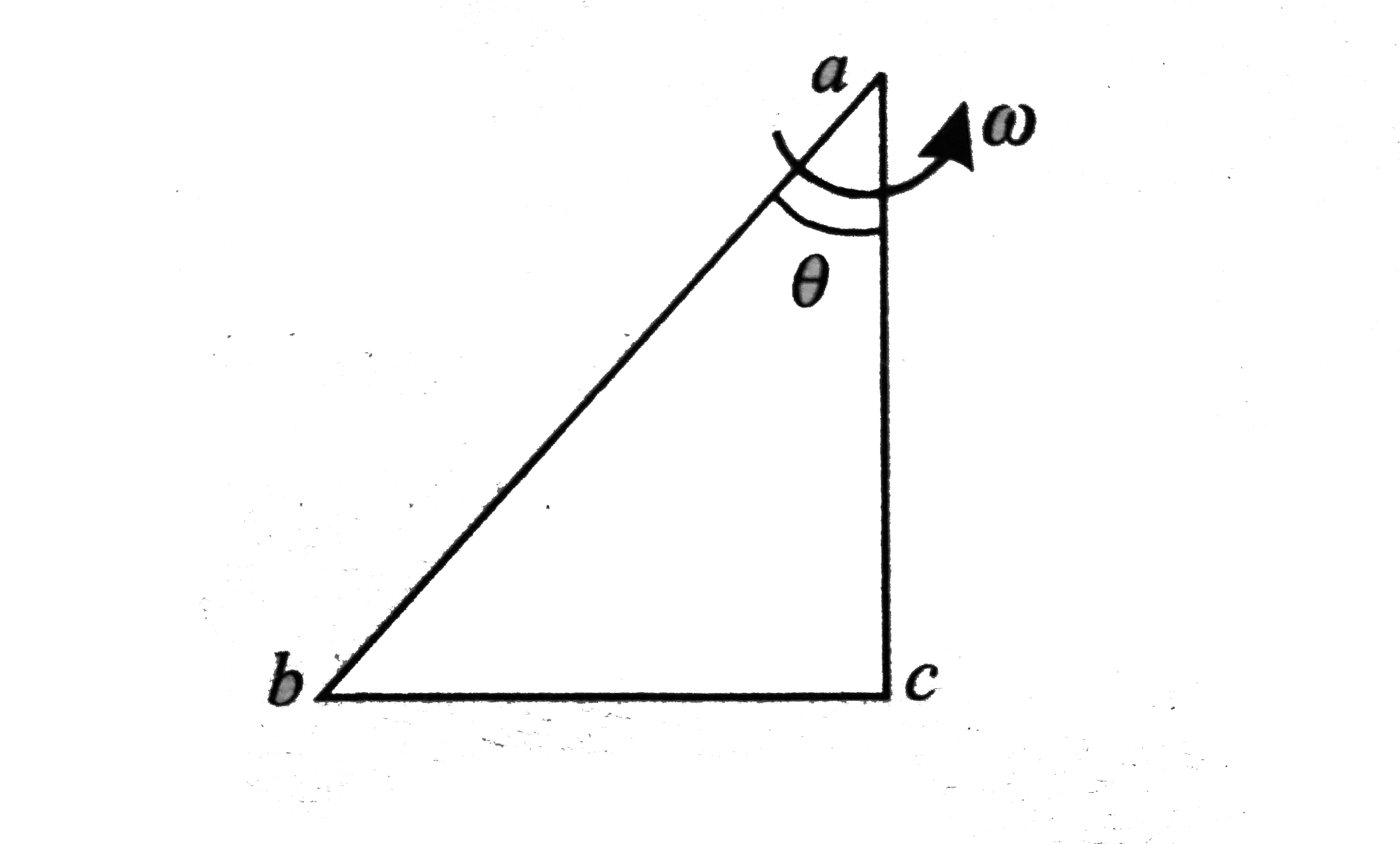
A rod of length L rotates in the form of a conical pendulum with an Angular velocity ω about its axis as shown in Fig. 3.165. The rod makes an angle θ with the axis. The magnitude of the motional emf developed across the two emf of the rod is

(a) 12BωL2
(b) 12BωL2tan2θ
( c) 12BωL2cos2θ
(d) 12BωL2sin2θ
The correct Answer is:D
(d) ε=∫(→v×→B).→dl

→ε=∫[(lsinθ)ωˆk)×B(−ˆj)].[dlsinθ(−ˆi)+dlcosθ(−gat(j))]
→ε=∫[Bωsinθ−ˆi].[dlsinθ(−ˆi)+dlcosθ(−ˆj)]
=−Bωsin2θ∫L0ldl=−12Bωsin2θL2
→ε=Vb−Va=−12BωL2sin2θ
Negative sign indicates that end b will be negative w.r.t.a.
Alternate Method:
Consider two more conductors ac and bc. This comletes a closed loop. The net emf inducd in this closed loop should be zero, as net flux through this loop always remains zero.
eab+ebc+eca=0
but ebc=12Bω(Lsinθ)2,eca=0 putting the values, we get
eab=−12Bω(Lsinθ)2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
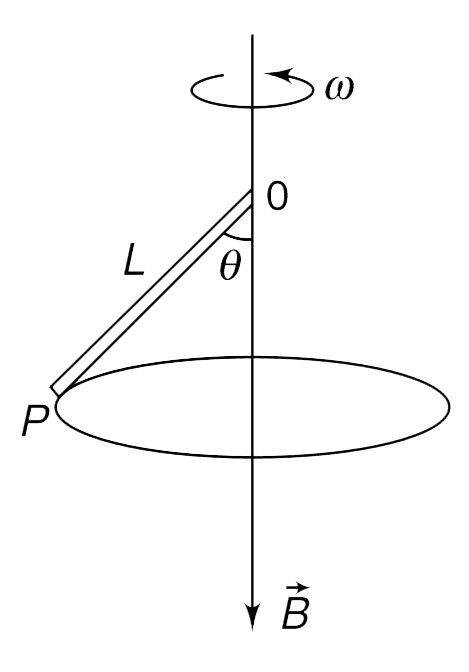
A conducting rod (OP) of length L rotates in form of a conical pendulum with an angular velocity ω about a fixed vertical axis passing through its end O. There is a uni- form magnetic field B in vertically downward direction. The rod makes an angle θ with the direction of the magnetic field. Calculate the emf induced across the ends of the rod. Which end is positive?
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
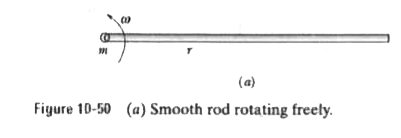
View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
A copper rod of length l rotates an angular velocity ω in a uniform magnetic field B as show in figure . What is the induced emf across its ends ?
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.

View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
View Solution
