A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
To solve the problem of a rod of mass M and length L being struck by a particle of mass m moving perpendicular to the rod, we will use the principles of conservation of linear momentum and conservation of angular momentum.
1. Identify Initial Conditions:
- The rod is initially at rest on a frictionless surface.
- The particle of mass m is moving with a velocity v perpendicular to the rod.
2. Conservation of Linear Momentum:
- The initial momentum of the system (only the particle is moving) is given by:
pi=mv
- After the collision, the combined system (rod + particle) will have a center of mass velocity Vcm. The total mass of the system is M+m.
- Thus, the final momentum of the system is:
pf=(M+m)Vcm
- By conservation of momentum:
mv=(M+m)Vcm(1)
3. Determine the Angular Momentum:
- The angular momentum before the collision is due to the particle striking the rod. The distance from the pivot (the end of the rod) to the line of action of the particle's momentum is L2.
- The initial angular momentum Li is:
Li=mv(L2)
- After the collision, the system rotates about the center of mass. The angular momentum Lf of the system after the collision can be expressed as:
Lf=Icmω+m(Vcm+ωL2)(L2)
- Here, Icm is the moment of inertia of the system about the center of mass.
4. Calculate the Moment of Inertia:
- The moment of inertia of the rod about its end is:
Irod=13ML2
- The moment of inertia of the particle at a distance L from the pivot is:
Iparticle=mL2
- Therefore, the total moment of inertia Icm is:
Icm=13ML2+mL2
5. Setting Up the Angular Momentum Equation:
- By conservation of angular momentum:
mv(L2)=(13ML2+mL2)ω+m(Vcm+ωL2)(L2)
6. Substituting Vcm:
- From equation (1), we can express Vcm:
Vcm=mvM+m
- Substitute Vcm into the angular momentum equation and solve for ω.
7. Final Expression for Angular Velocity:
- After simplification, we find:
ω=6mv(M+4m)L
Final Answer:
The angular velocity ω acquired by the combined system is:
ω=6mv(M+4m)L
- The rod is initially at rest on a frictionless surface.
- The particle of mass m is moving with a velocity v perpendicular to the rod.
- The initial momentum of the system (only the particle is moving) is given by:
pi=mv
- After the collision, the combined system (rod + particle) will have a center of mass velocity Vcm. The total mass of the system is M+m.
- Thus, the final momentum of the system is:
pf=(M+m)Vcm
- By conservation of momentum:
mv=(M+m)Vcm(1)
- The angular momentum before the collision is due to the particle striking the rod. The distance from the pivot (the end of the rod) to the line of action of the particle's momentum is L2.
- The initial angular momentum Li is:
Li=mv(L2)
- After the collision, the system rotates about the center of mass. The angular momentum Lf of the system after the collision can be expressed as:
Lf=Icmω+m(Vcm+ωL2)(L2)
- Here, Icm is the moment of inertia of the system about the center of mass.
- The moment of inertia of the rod about its end is:
Irod=13ML2
- The moment of inertia of the particle at a distance L from the pivot is:
Iparticle=mL2
- Therefore, the total moment of inertia Icm is:
Icm=13ML2+mL2
- By conservation of angular momentum:
mv(L2)=(13ML2+mL2)ω+m(Vcm+ωL2)(L2)
- From equation (1), we can express Vcm:
Vcm=mvM+m
- Substitute Vcm into the angular momentum equation and solve for ω.
- After simplification, we find:
ω=6mv(M+4m)L
The angular velocity ω acquired by the combined system is:
ω=6mv(M+4m)L
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View Solution
Knowledge Check
A rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
A3√2V7LB√2V7LC√2V3LD3V7LA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 A6v05LB12v05LC2v05LD3v07L
A6v05LB12v05LC2v05LD3v07LA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is vlBangular velocity of the system after collision is v2lCthe loss in kinetic enerlgy of the system as a whole as a result of the collision is mv26Dthe loss in kinetic energy of the system as a whole as a result of the collision is 7mv224
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.
View SolutionTwo particles A and B, each of mass m, are connected by a light rod of length L lying on a smooth horizontal surface. A particle of mass m moving with speed v0 strikes to the end of rod and sticks to A as shown . Find
(a) the velocity of the center of mass,
(b) the angular velocity about the center of mass of system (A+B+ particle) and
(c) the linear speeds of A and B immediately after collision.
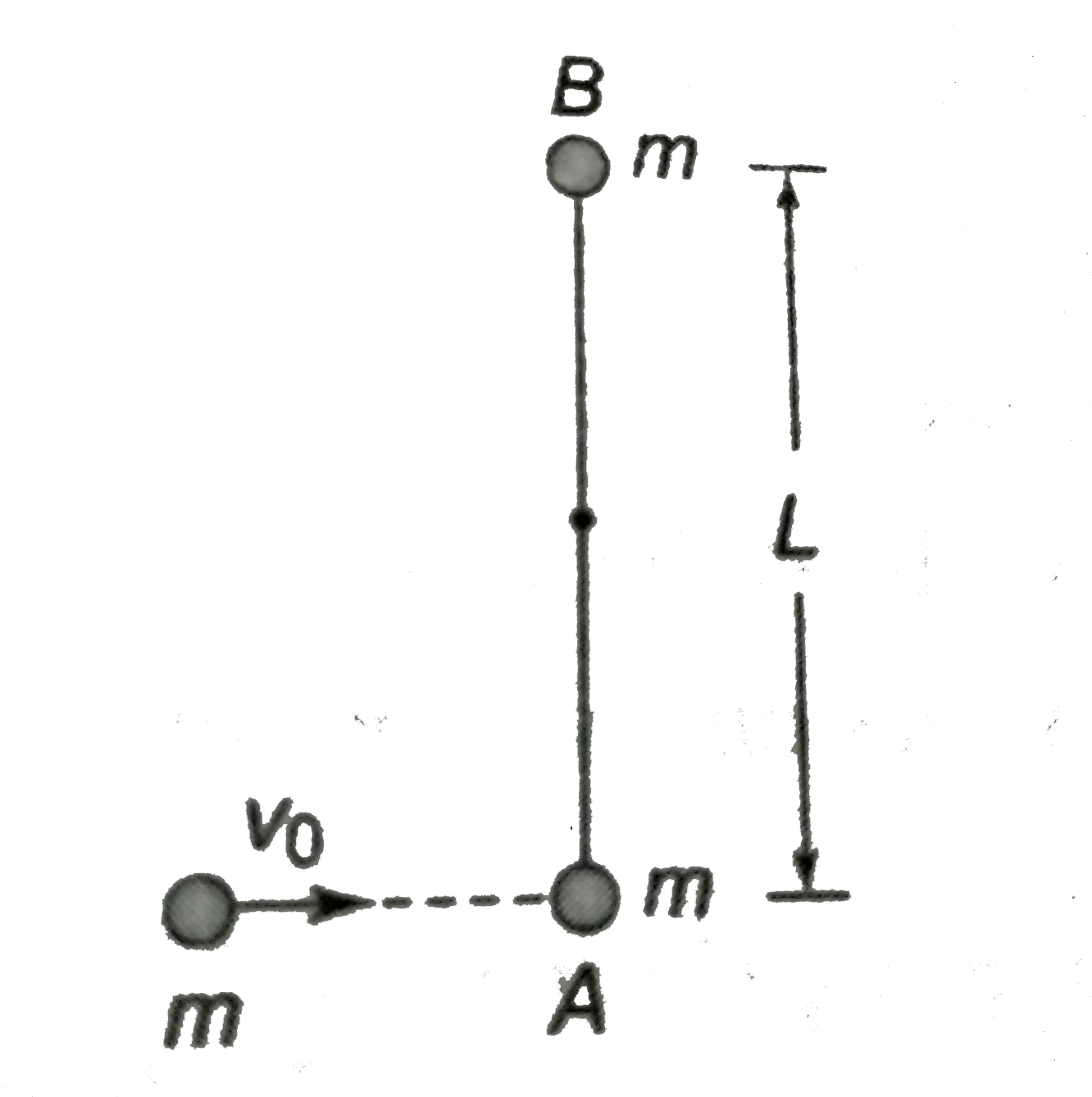
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end. A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
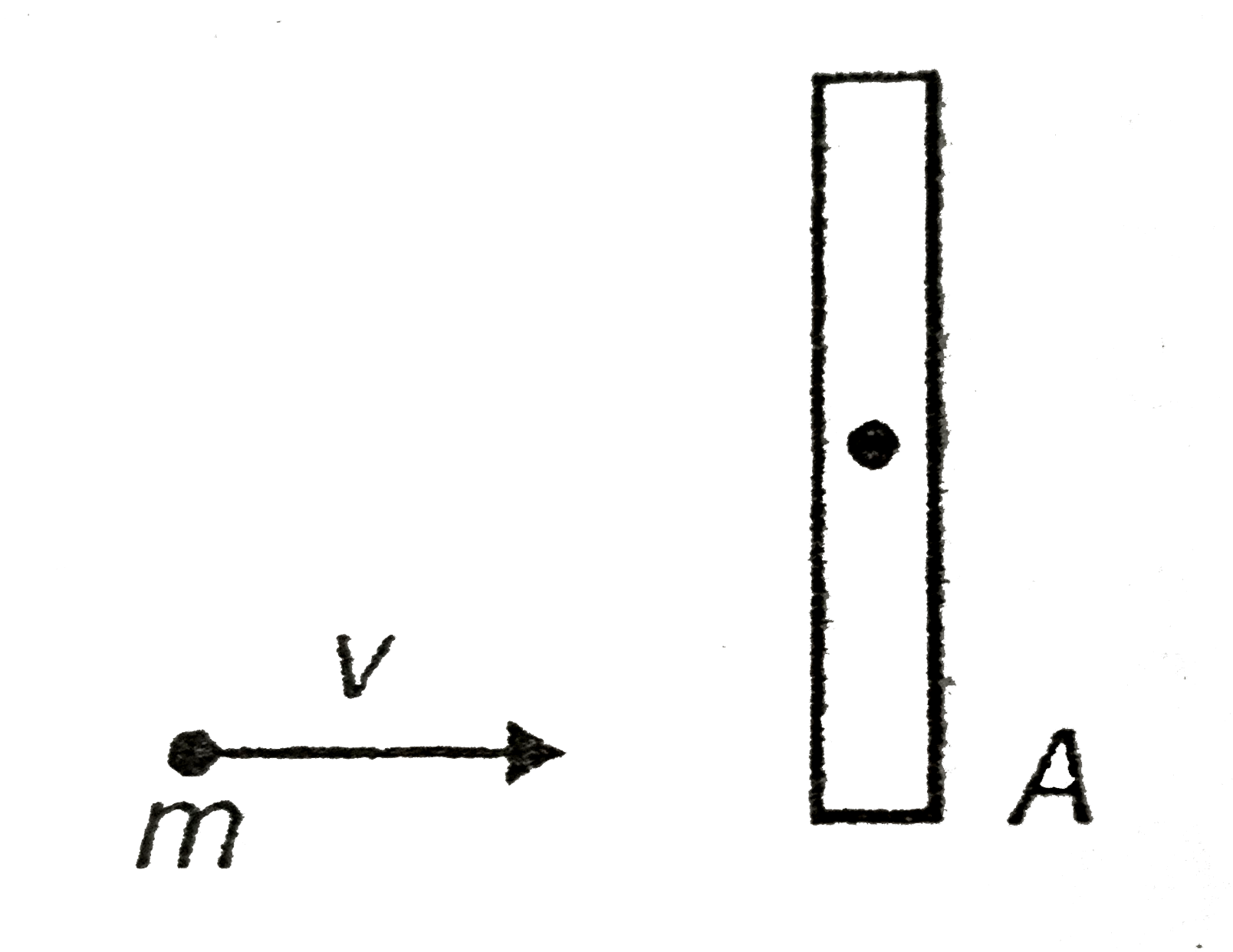
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View Solution
