A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficeint between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

Forces acting on the rod are as shown in the figure.
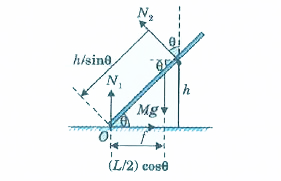
Roller is smooth so only normal force N2 acts perpendicular to the rod. N1 and f are normal reaction and friction from the floor. Mg is weight of rod acting at a distance L/2 from the bottom end O.
The is a case of equilibrium.
Vertical equilibrium ⇒N1+N2cosθ=Mg ......(i)
Horizontal equilibrium ⇒f=N2sinθ ......(ii)
Rotational equilibrium about point O
⇒N2hsinθ=MgL2cosθ
⇒N2=MgLsinθcosθ2h ......(iii)
Substituting equation (iii) in equation (i) we get the following:
⇒N1+(MgLsinθcosθ2h)cosθ=Mg
⇒N1=Mg=MgLsinθcos2θ2h .....(iv)
Rod is on the verge of slipping.
f=μN1
Using equation (ii) we can rewrite the above relation as following:
N2sinθ=μN1
Substituting from equations (iii) and (iv) we get the following:
MgLsinθcosθ2hsinθ=μ(Mg−MgLsinθcos2θ2h)
⇒μ=Lcosθsin2θ2h−Lcos2θsinθ
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

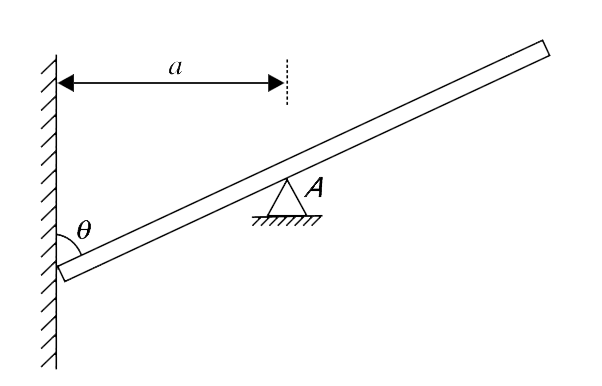
View SolutionA uniform rod of length b can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is μ. Distance of support from the wall is a.
(a) Find the ratio ab if the maximum value of θ is θ1.
(b) Find the ratio ab if the minimum value of θ is θ2.
View Solution
Knowledge Check
A uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of theseA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.A(√2−1)mgB(√2+1)mgC(√3+1)mgD(√2+3)mgA uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
Aits center of mass moves vertically downwards on a straight lineBIts center of mass remains in restCthe rod rotates about a vertical axisDBoth a and c are correct
A uniform rod of length 1m having mass 1kg rests against a smooth wall at an angle of 30∘ with the ground. Calculate the force exerted by the ground on the rod. Take g=10ms−2.
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
View SolutionThere is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
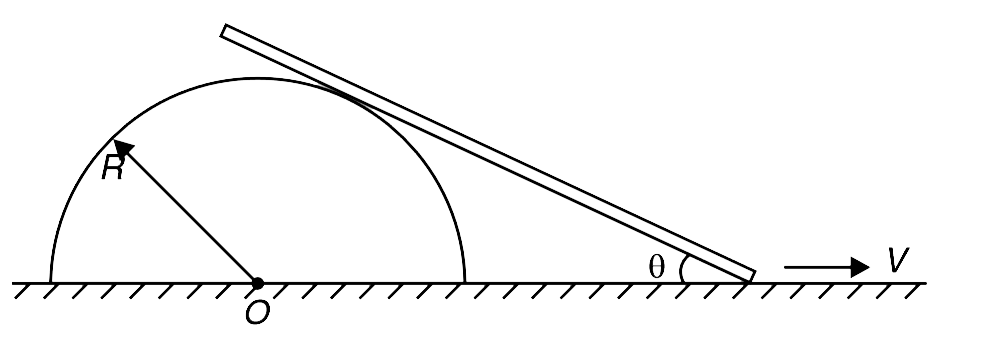
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View Solution