A rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
To solve the problem, we need to analyze the collision between the particle and the rod, applying the principles of conservation of momentum and conservation of angular momentum. Here’s a step-by-step solution:
Step 1: Understand the System
We have a rod of mass m and length L resting on a frictionless surface. A particle of mass m is moving with speed v and strikes the end of the rod perpendicularly.
Step 2: Conservation of Linear Momentum
Since there are no external forces acting on the system, the linear momentum before and after the collision must be conserved.
Initial momentum Pi:
Pi=mv
Final momentum Pf:
Pf=mu+mvcm
where u is the velocity of the particle after the collision, and vcm is the velocity of the center of mass of the rod after the collision.
Setting initial momentum equal to final momentum:
mv=mu+mvcm
We can simplify this to:
v=u+vcm(Equation 1)
Step 3: Conservation of Angular Momentum
Next, we apply the conservation of angular momentum about the center of mass of the rod. The initial angular momentum Li is due to the particle striking the rod.
Initial angular momentum:
Li=mv⋅L2
Final angular momentum Lf:
Lf=mvcm⋅L2+Icmω
where Icm is the moment of inertia of the rod about its center of mass, which is 112mL2, and ω is the angular velocity of the rod.
Setting initial angular momentum equal to final angular momentum:
mv⋅L2=mvcm⋅L2+112mL2ω(Equation 2)
Step 4: Coefficient of Restitution
Given that the coefficient of restitution e=1, we can relate the velocities before and after the collision:
e=Velocity of separationVelocity of approach
The velocity of separation is:
vcm+L2ω−u
The velocity of approach is:
v
Setting up the equation:
vcm+L2ω−u=v(Equation 3)
Step 5: Solve the Equations
Now we have three equations (1, 2, and 3) with three unknowns: u, vcm, and ω.
From Equation 1:
u=v−vcm(Substituting into Equation 2)
Substituting u into Equation 2:
mv⋅L2=mvcm⋅L2+112mL2ω
Cancelling m and rearranging gives:
v⋅L2−vcm⋅L2=112L2ω
Now substituting vcm from Equation 1 into this equation will allow us to solve for ω.
After some algebra, we find:
ω=12v5L
Final Answer
The angular velocity ω acquired by the rod is:
ω=12v5L
We have a rod of mass m and length L resting on a frictionless surface. A particle of mass m is moving with speed v and strikes the end of the rod perpendicularly.
Since there are no external forces acting on the system, the linear momentum before and after the collision must be conserved.
Pi=mv
Pf=mu+mvcm
where u is the velocity of the particle after the collision, and vcm is the velocity of the center of mass of the rod after the collision.
mv=mu+mvcm
We can simplify this to:
v=u+vcm(Equation 1)
Next, we apply the conservation of angular momentum about the center of mass of the rod. The initial angular momentum Li is due to the particle striking the rod.
Li=mv⋅L2
Lf=mvcm⋅L2+Icmω
where Icm is the moment of inertia of the rod about its center of mass, which is 112mL2, and ω is the angular velocity of the rod.
mv⋅L2=mvcm⋅L2+112mL2ω(Equation 2)
Given that the coefficient of restitution e=1, we can relate the velocities before and after the collision:
e=Velocity of separationVelocity of approach
vcm+L2ω−u
The velocity of approach is:
v
vcm+L2ω−u=v(Equation 3)
Now we have three equations (1, 2, and 3) with three unknowns: u, vcm, and ω.
u=v−vcm(Substituting into Equation 2)
mv⋅L2=mvcm⋅L2+112mL2ω
Cancelling m and rearranging gives:
v⋅L2−vcm⋅L2=112L2ω
ω=12v5L
The angular velocity ω acquired by the rod is:
ω=12v5L
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View Solution
Knowledge Check
A uniform rod of mass m and length L is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass m collides with the rod with a speed V0. The coefficient of restitution for the collision is e=12. If hinge reaction during the collision is zero then the value of x is :
 ANo such value of x is possibleBx=L2Cx=2L3Dx=L
ANo such value of x is possibleBx=L2Cx=2L3Dx=LA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 A6v05LB12v05LC2v05LD3v07L
A6v05LB12v05LC2v05LD3v07LA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.
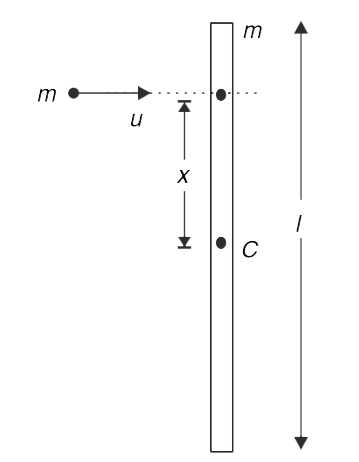
View SolutionA uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x=l√6 from the centre C of the rod. Collision is elastic.
(a) Find the speed of the centre of the rod and the particle after the collision.
(b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision?
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View Solution
