A rod of mass m is supported on a wedge of mass M shown in fig. Find the accelerations of rod a and wedge A in the arrangment. The friction between all contact surfaces in negligible.

The rod is constrained to move in the vertical direction (with the help of the guids) and the wedge will move along the surface in the horizontal direction. Initially, the system is held at rest.
Constraint relation: Approach 1 Let the acceleration of m w.r.t gound be a vertically downwards and acceleration of M w.r.t ground be A horizontally towards right.
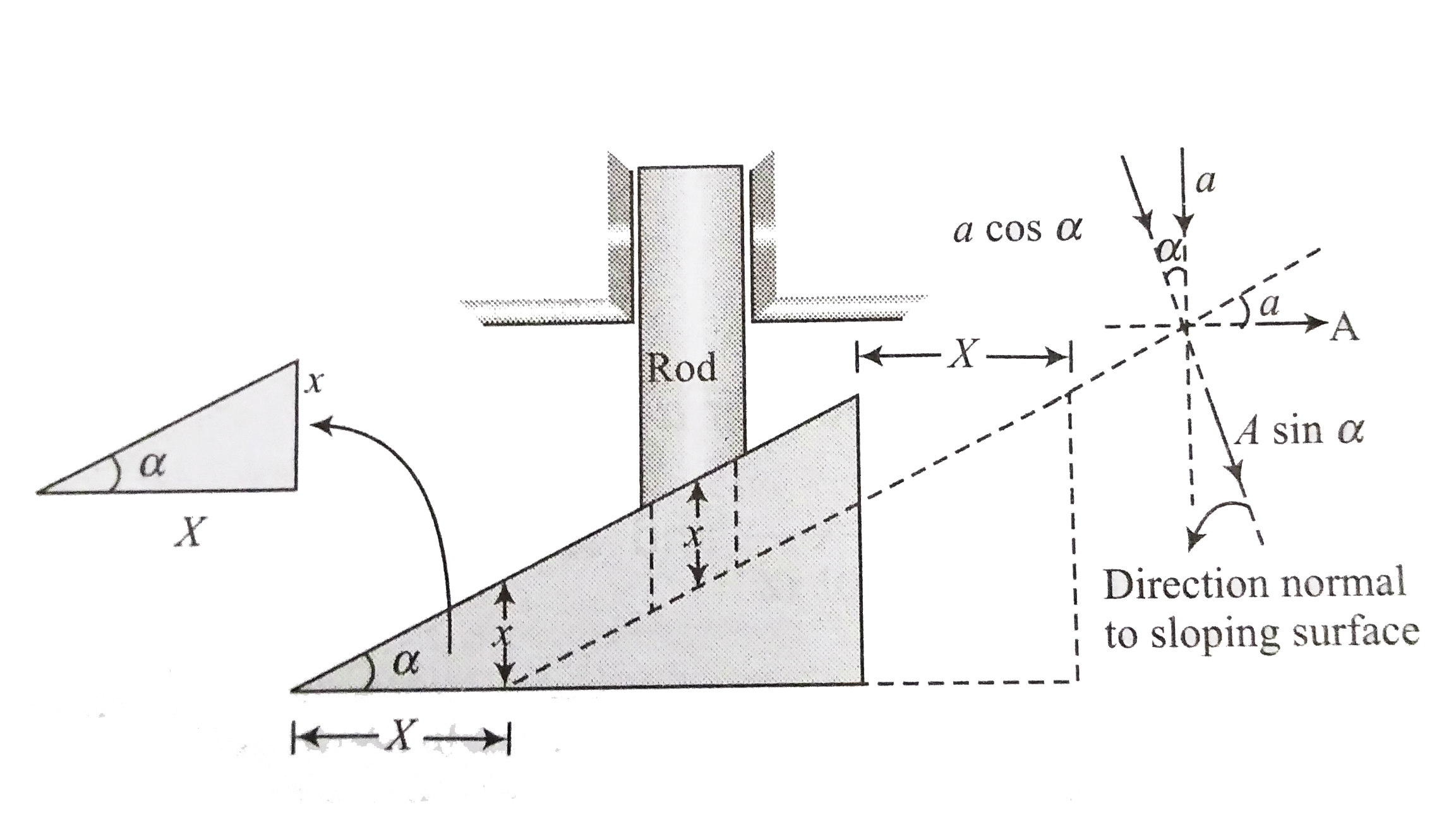
The motion of the system is constrained by the fact that the "bottom face of the rod must always be in contact with the inclined plane. If in time t, X is the displacement of the wedge and x is the displacement of the rod, then the constraint demands that
From fig. we have xX=tanα
∴x=Xtanα ...(i) Here α remains constant.
Differentating (i) w.r.t twice, we get
(d2xdt2)=(d2Xdt2)tanα [tanα=constant]
Hence, a=Atanα
Approch 2: The fact that the rod (or a particle on the wedge and the wedge must not lose contact is usually called wedge constraints. For this, the component of the acceleration of the rod perpendicular to the wedge plane = component of acceleration of the wedge perpendicular to wedge plane.
acosα=Asinα⇒a=Atanα
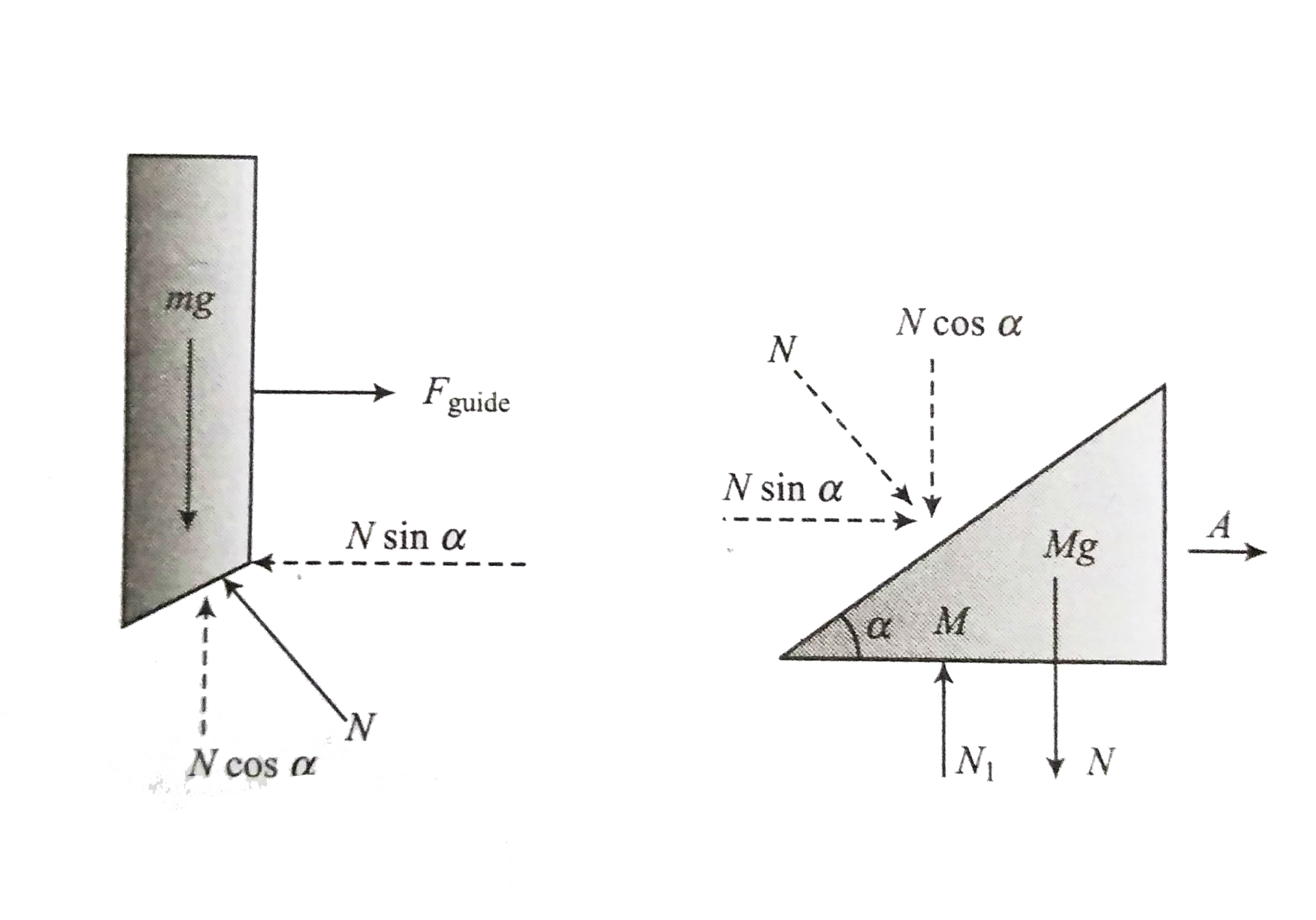
The force acting on the rod are:
 ,
,
∗ The weight mg, vertically downwars
∗ The normal force N, normal to the bottom surface of the horizontal component of N as for the rod ahorizontal=0.
Motion in vertical direction
mg−Ncosα=ma...(ii)
and the force acting on the wedge are
⋅ The weight, Mg
∗ N, reaction of N acting on the rod
∗N1, Normal force by the surface
The force equation are
N1−Mg−Ncosα=0 ...(iii)
and Nsinα=MA ...(iv)
Solving the above equation for a and A, we get
a=mgtanαmtanα+Ncotα and Amgmtanα+Mcotα.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Find the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.

View SolutionA rod 'A' constrained to move in vertical direction rests on a wedge B, as shown in the Fig. Find the accelerations of rod A and wedge B instantaneously after system is released from rest, neglecting friction at all the contact surfaces.
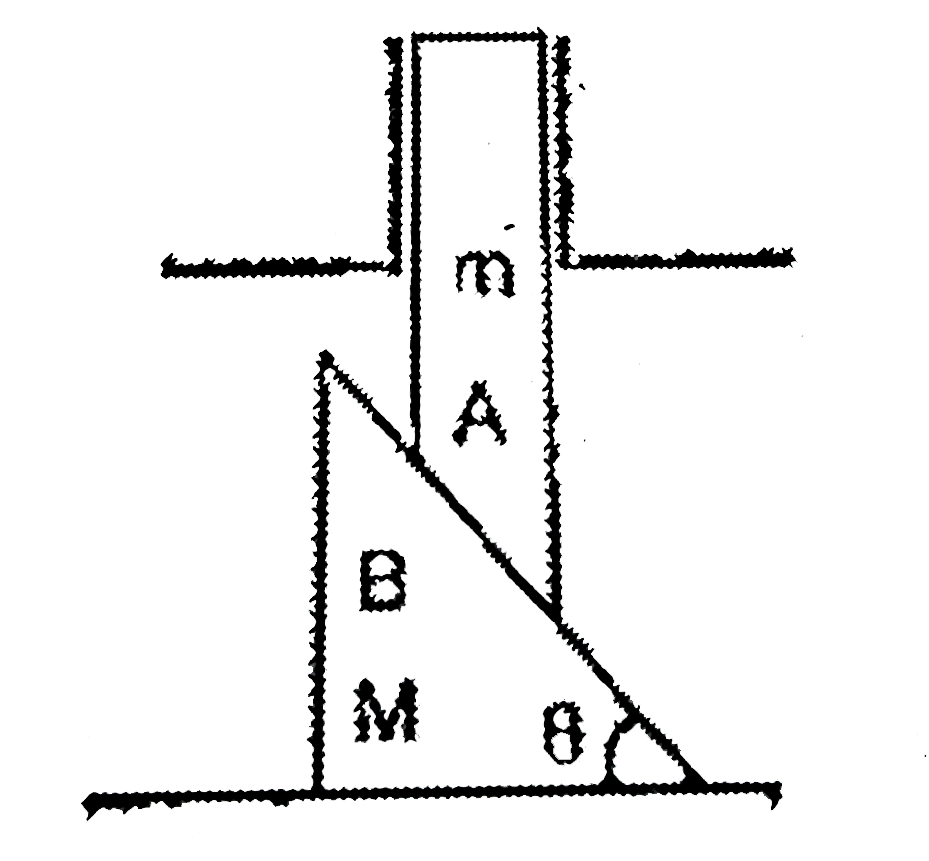
View Solution
Knowledge Check
A block of mass m=5kg is placed on the wedge of mass M=32kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. Spring and pulley are ideal)
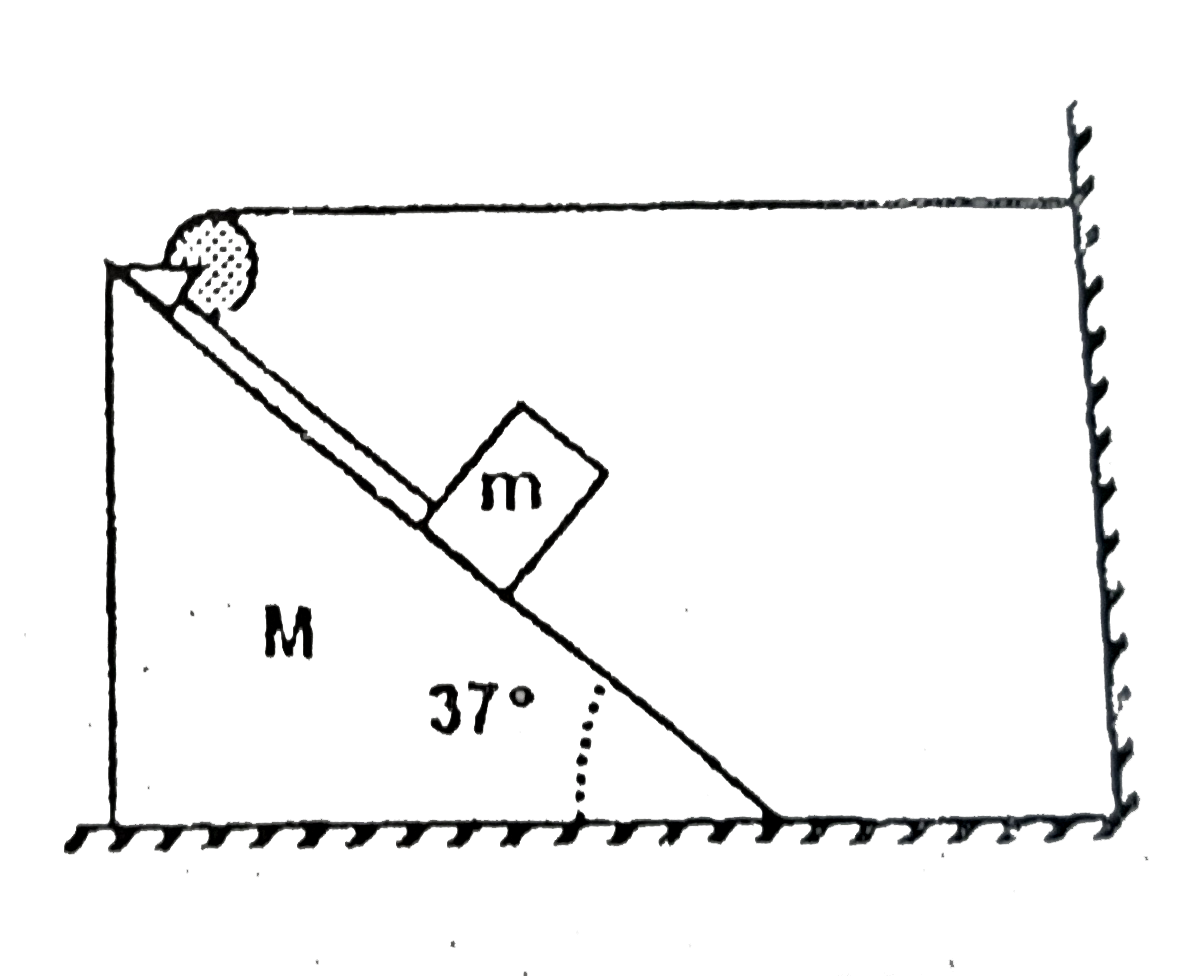 A12m/s2B34m/s2C43m/s2D35m/s2
A12m/s2B34m/s2C43m/s2D35m/s2A block of mass m=5 kg is placed on the wedge of mass M=32 kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. String and pulley are ideal )
 A12m/s2B35m/s2C43m/s2D34m/s2
A12m/s2B35m/s2C43m/s2D34m/s2All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
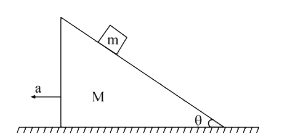 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
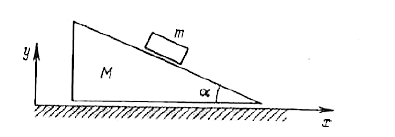
A block of mass m is placed on wedge of mass M (Fig.). Find the accelerations of the block and the wedge in the reference system fixed to the table, and the reaction. Friction is to be neglected.
Analyse the limiting case when the wedge remains stationary.
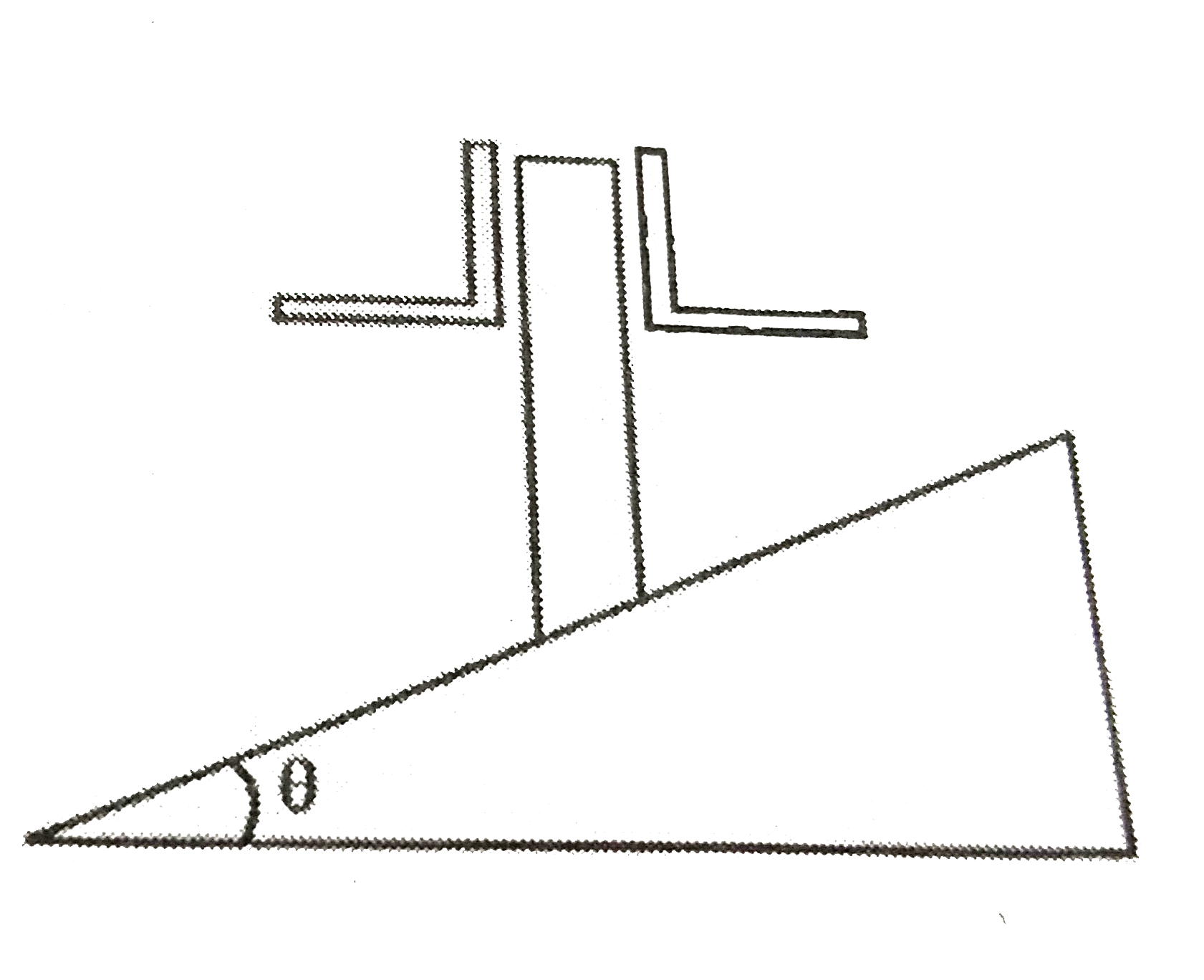
View SolutionFind the acceleration of rod A and wedge B in the arrangement shown in fig if the ratio of the mass of wedge to that of the rod equals η and the friction between the contact surfaces are negligible.
View SolutionFind the acceleration of rod A and wedge B in the arrangement shown in figure if the mass of rod equal that of the wedge and the friction between all contact surfaces is negligible Take angle of wedge as 45∘&g=9.8m/s2

View SolutionA plank of mass m rests symmetrically on two wedges B and C of mass M. What is the acceleration of the plank? Neglect friction between all the contact surfaces.

View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
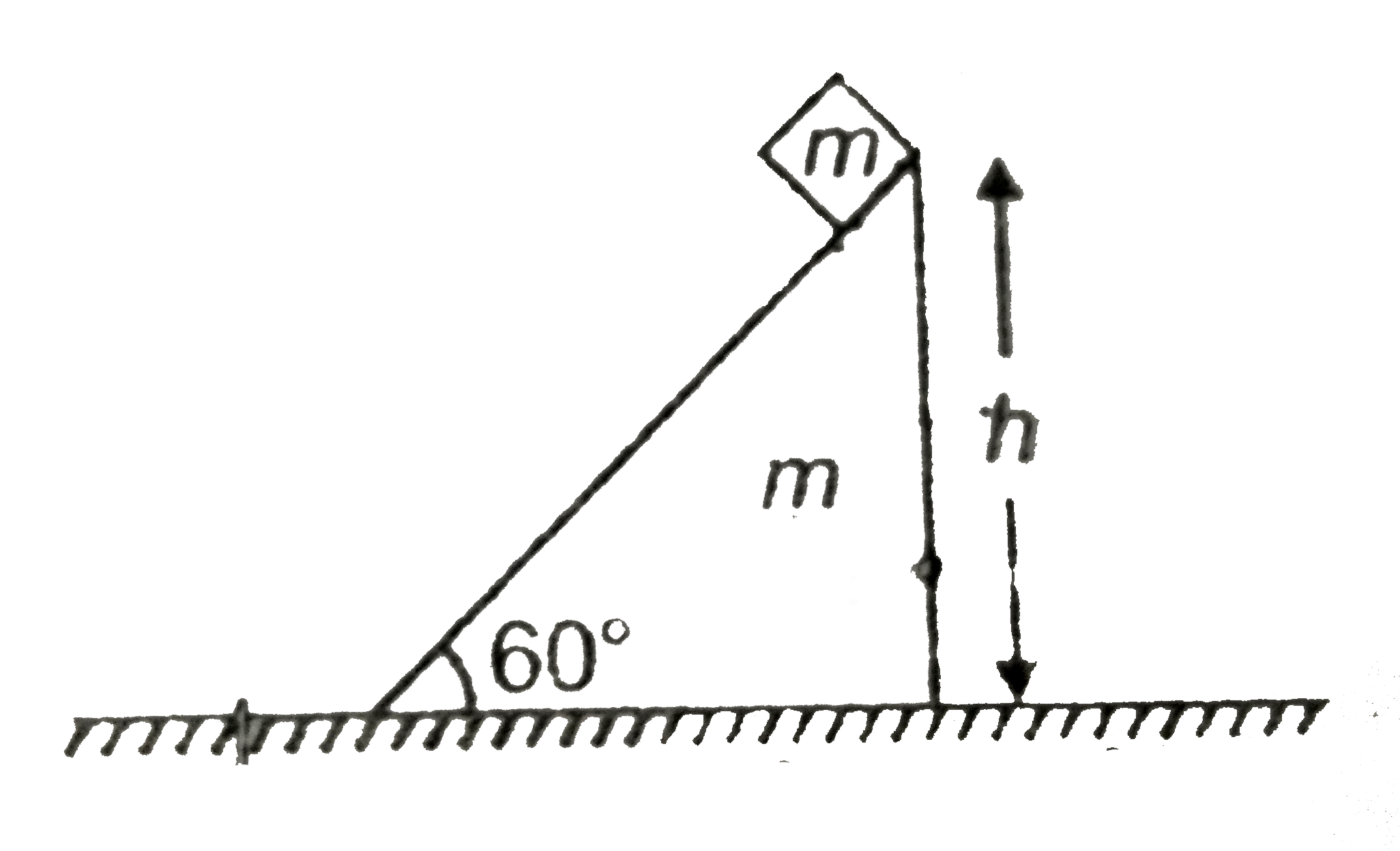
View Solution
