A rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. However, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
2ML29
3ML216
7ML218
none of these
The correct Answer is:C

S= area of cross-section
ρx=ρ0+(2ρ0−ρ0L)x=ρ0+ρ0Lx
Now, M=∫L0dM=∫L0(Sdx)(ρ0+ρ0Lx)
=ρ0S(3L2)
∴ρ0S=2M3L ..(i)
Now, I=∫L0dI=∫L0(dM)x2
=∫L0(Sdx)(ρ0+ρ0Lx)(x2)
After substituting velue of ρ0S from eq (i) then we find
I=718ML2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View Solution
Knowledge Check
The moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
AI4BI2C2ID4IMoment of inertia of a thin uniform rod about an axis passing through one end perpendicular to its length is I . Then moment of inertia the same rod about the central axis perpendicular to its plane is
AI/4B2IC4ID3 IThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
AI4BI2C2ID4I
The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
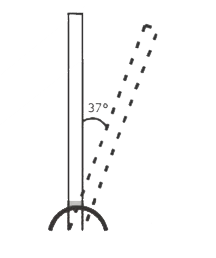
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionIn the figure a uniform rod of mass 'm' and length 'l' is hinged at one end and the other end is connected to a light vertical of spring constant 'k' as shown in figure. The spring has extension such that rod is equilibrium when it is horizontal . The rod rotate about horizontal axis passing through end 'B'. Neglecting friction at the hinge find (a) extension in the spring (b) the force on the rod due to hinge.
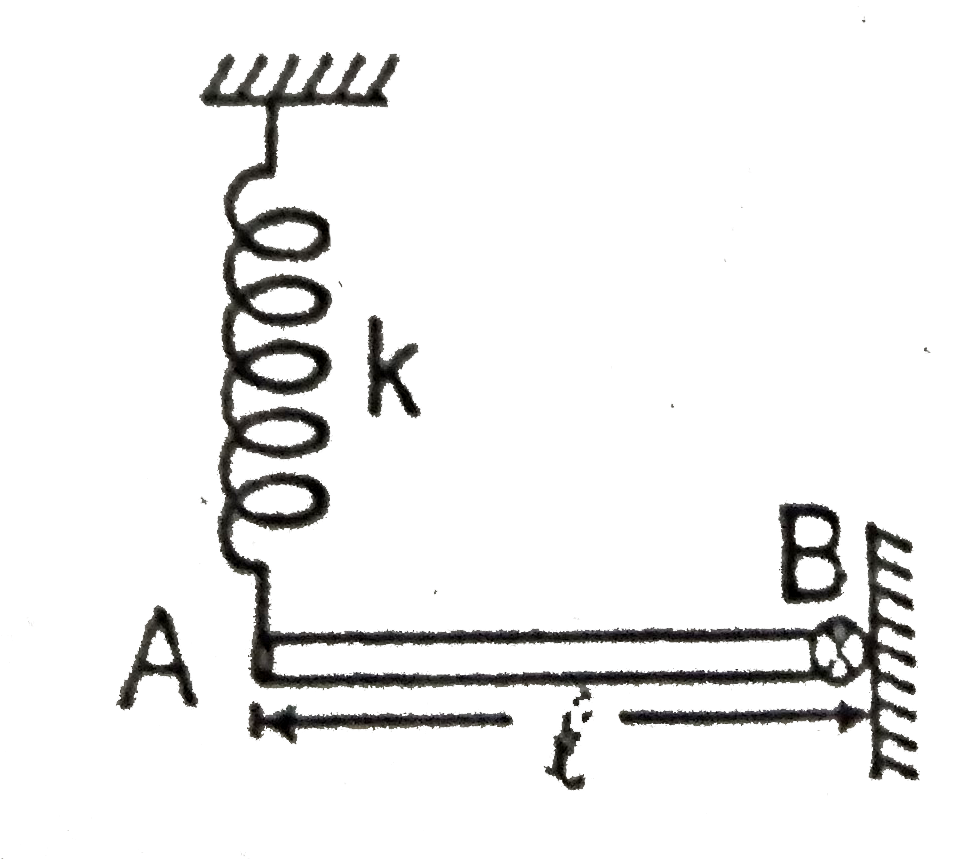
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View Solution
