A rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient offriction between chain and inclined plane is μ, the maximum length of the lianging part to prevent the chain from falling vertically is:
To solve the problem of finding the maximum length of the hanging part of a chain on a rough inclined plane, we can follow these steps:
Step 1: Understand the System
We have a uniform chain of length L that is partially on an inclined plane inclined at 30∘ to the horizontal and partially hanging off the edge. We need to find the maximum length X of the hanging part of the chain such that it does not fall vertically.
Step 2: Define Variables
Let:
- X = length of the hanging part of the chain
- L−X = length of the part of the chain on the inclined plane
- M = mass of the entire chain
- m=XLM = mass of the hanging part of the chain
- M−m=L−XLM = mass of the part on the incline
Step 3: Forces Acting on the Chain
1. The weight of the hanging part of the chain is Wh=m⋅g=XLMg.
2. The weight of the part on the incline is Wi=(M−m)⋅g=(1−XL)Mg.
Step 4: Frictional Force
The frictional force Ff acting on the part of the chain on the incline can be calculated as:
Ff=μ⋅N
where N is the normal force. The normal force is equal to the component of the weight of the chain on the incline:
N=(M−m)gcos(30∘)=(1−XL)Mg⋅√32
Thus,
Ff=μ⋅(1−XL)Mg⋅√32
Step 5: Balance Forces
For the chain to be in equilibrium and not fall, the tension T in the chain must balance the forces acting on it:
T=Wh=XLMg
And the forces acting downwards due to the weight of the chain on the incline and friction must be equal to the tension:
T=Wi⋅sin(30∘)+Ff
Substituting the expressions we have:
XLMg=(1−XL)Mg⋅12+μ⋅(1−XL)Mg⋅√32
Step 6: Simplifying the Equation
Cancel Mg from both sides:
XL=(1−XL)(12+μ⋅√32)
Let k=12+μ⋅√32:
XL=(1−XL)k
Let y=XL:
y=(1−y)k
y+ky=k
y(1+k)=k
y=k1+k
Step 7: Substitute Back for X
Thus, the maximum length of the hanging part is:
X=L⋅12+μ⋅√321+(12+μ⋅√32)
Final Answer
The maximum length of the hanging part of the chain X is given by:
X=L(12+μ⋅√32)1+12+μ⋅√32
We have a uniform chain of length L that is partially on an inclined plane inclined at 30∘ to the horizontal and partially hanging off the edge. We need to find the maximum length X of the hanging part of the chain such that it does not fall vertically.
Let:
- X = length of the hanging part of the chain
- L−X = length of the part of the chain on the inclined plane
- M = mass of the entire chain
- m=XLM = mass of the hanging part of the chain
- M−m=L−XLM = mass of the part on the incline
1. The weight of the hanging part of the chain is Wh=m⋅g=XLMg.
2. The weight of the part on the incline is Wi=(M−m)⋅g=(1−XL)Mg.
The frictional force Ff acting on the part of the chain on the incline can be calculated as:
Ff=μ⋅N
where N is the normal force. The normal force is equal to the component of the weight of the chain on the incline:
N=(M−m)gcos(30∘)=(1−XL)Mg⋅√32
Thus,
Ff=μ⋅(1−XL)Mg⋅√32
For the chain to be in equilibrium and not fall, the tension T in the chain must balance the forces acting on it:
T=Wh=XLMg
And the forces acting downwards due to the weight of the chain on the incline and friction must be equal to the tension:
T=Wi⋅sin(30∘)+Ff
Substituting the expressions we have:
XLMg=(1−XL)Mg⋅12+μ⋅(1−XL)Mg⋅√32
Cancel Mg from both sides:
XL=(1−XL)(12+μ⋅√32)
Let k=12+μ⋅√32:
XL=(1−XL)k
Let y=XL:
y=(1−y)k
y+ky=k
y(1+k)=k
y=k1+k
Thus, the maximum length of the hanging part is:
X=L⋅12+μ⋅√321+(12+μ⋅√32)
The maximum length of the hanging part of the chain X is given by:
X=L(12+μ⋅√32)1+12+μ⋅√32
Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block is given velocity 10 m/s along the fixed inclined as shown in figure from the bottom of the inclined plane. Find the total distance travelled along the inclined plane. If the coefficient of friction is equal to 0.5

View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
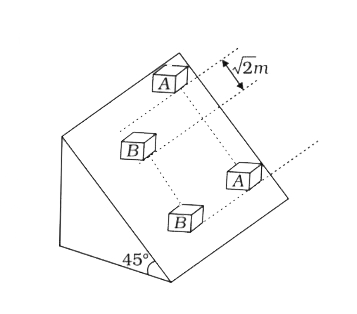
View SolutionA ball is dropped on a smooth inclined plane and is observed to move horizontally after the impact. The coefficient of restitution between the plane and ball is e. The inclination of the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is the 1/√3. What is the acceleration of the block ?
View SolutionAn inclined plane is inclined at θ with horizontal as shown in (figure).Write a unit vector in the direction parallel (ˆa) and perpendicular (ˆb) to inclined plane,in standard xy coordinate system.
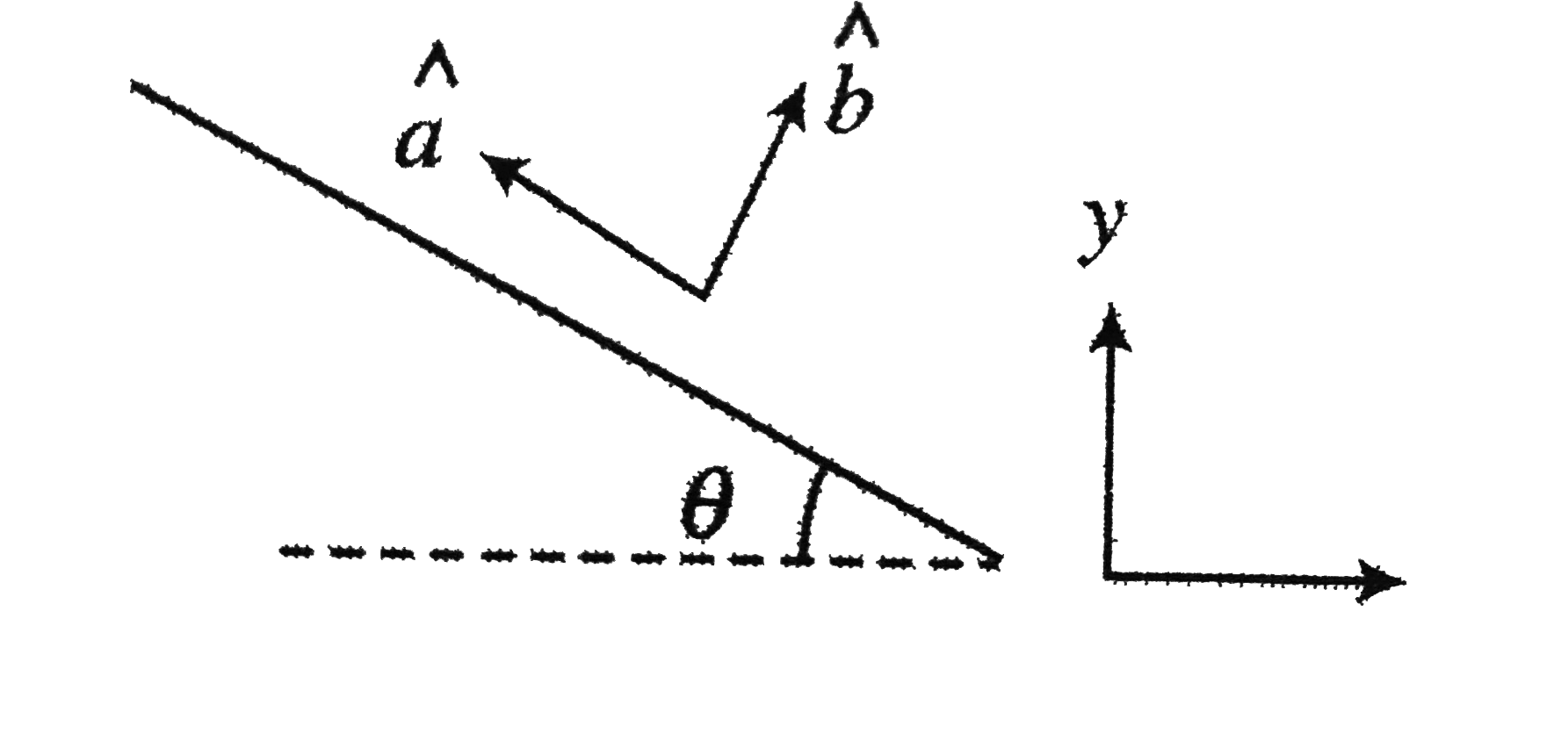
View Solution
