A particle starts from rest from the top of an inclined plane and again comes to rest on reaching the bottom most point of the inclined plane. If the coefficient of friction on some part of inclined plane is 3tanθ and rest portion is smooth then the ratio of the rough length of the inclined to smooth length is 1:n1 then value of n is .....?
The correct Answer is:6
To solve the problem, we need to analyze the motion of the particle on the inclined plane, considering the effects of friction and the smooth portion of the incline. Here’s the step-by-step solution:
Step 1: Understand the Setup
The particle starts from rest at the top of an inclined plane and comes to rest at the bottom. There are two sections of the incline: a rough section with a coefficient of friction of 3tanθ and a smooth section.
Step 2: Define Variables
Let:
- L = length of the rough portion
- nL = length of the smooth portion (where n is the ratio we need to find)
- g = acceleration due to gravity
- θ = angle of the incline
Step 3: Forces Acting on the Particle
On the rough portion:
- The gravitational force component along the incline: mgsinθ
- The frictional force opposing the motion: f=μN=3tanθ⋅mgcosθ
Where N=mgcosθ is the normal force.
Step 4: Net Force on the Rough Portion
The net force acting on the particle while it is on the rough portion can be expressed as:
Fnet=mgsinθ−f=mgsinθ−3tanθ⋅mgcosθ
Fnet=mgsinθ−3mgsinθcosθcosθ=mgsinθ−3mgsinθ=−2mgsinθ
Step 5: Acceleration on the Rough Portion
Using Newton's second law, F=ma:
ma=−2mgsinθ
a=−2gsinθ
Step 6: Motion on the Rough Portion
Using the equation of motion v2=u2+2as for the rough portion where initial velocity u=0:
0=0+2(−2gsinθ)L
This gives us the final velocity at the end of the rough portion.
Step 7: Motion on the Smooth Portion
On the smooth portion, the only force acting is the component of gravity:
F=mgsinθ
The acceleration on this portion is:
a=gsinθ
Step 8: Using the Work-Energy Principle
The work done by gravity on the entire incline must equal the work done against friction on the rough portion:
Work done by gravity=mg(htotal)=mg(Lsinθ+nLsinθ)
Work done against friction=f⋅L=3tanθ⋅mgcosθ⋅L
Step 9: Setting Up the Equation
Equating the work done by gravity and work done against friction:
mg(L+nL)sinθ=3tanθ⋅mgcosθ⋅L
Cancelling mg from both sides:
(L+nL)sinθ=3tanθ⋅cosθ⋅L
Using tanθ=sinθcosθ:
(L+nL)sinθ=3sinθ⋅L
Step 10: Solving for n
Dividing both sides by sinθ (assuming sinθ≠0):
L+nL=3L
1+n=3
n=2
Final Answer
The value of n is 2.
---
The particle starts from rest at the top of an inclined plane and comes to rest at the bottom. There are two sections of the incline: a rough section with a coefficient of friction of 3tanθ and a smooth section.
Let:
- L = length of the rough portion
- nL = length of the smooth portion (where n is the ratio we need to find)
- g = acceleration due to gravity
- θ = angle of the incline
On the rough portion:
- The gravitational force component along the incline: mgsinθ
- The frictional force opposing the motion: f=μN=3tanθ⋅mgcosθ
The net force acting on the particle while it is on the rough portion can be expressed as:
Fnet=mgsinθ−f=mgsinθ−3tanθ⋅mgcosθ
Fnet=mgsinθ−3mgsinθcosθcosθ=mgsinθ−3mgsinθ=−2mgsinθ
Using Newton's second law, F=ma:
ma=−2mgsinθ
a=−2gsinθ
Using the equation of motion v2=u2+2as for the rough portion where initial velocity u=0:
0=0+2(−2gsinθ)L
This gives us the final velocity at the end of the rough portion.
On the smooth portion, the only force acting is the component of gravity:
F=mgsinθ
The acceleration on this portion is:
a=gsinθ
The work done by gravity on the entire incline must equal the work done against friction on the rough portion:
Work done by gravity=mg(htotal)=mg(Lsinθ+nLsinθ)
Work done against friction=f⋅L=3tanθ⋅mgcosθ⋅L
Equating the work done by gravity and work done against friction:
mg(L+nL)sinθ=3tanθ⋅mgcosθ⋅L
Cancelling mg from both sides:
(L+nL)sinθ=3tanθ⋅cosθ⋅L
Using tanθ=sinθcosθ:
(L+nL)sinθ=3sinθ⋅L
Dividing both sides by sinθ (assuming sinθ≠0):
L+nL=3L
1+n=3
n=2
The value of n is 2.
Topper's Solved these Questions
Similar Questions
If the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View SolutionA block is kept on a inclined plane of inclination q of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is μ
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m start slipping from top of inclined plane at B and comes to rest when reaches to lowest point A of inclined plane, if BC = 2AC and friction coefficient of part AC is 'mu = ktan(theta)' then find value of k
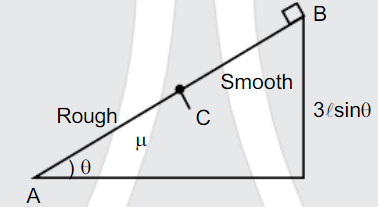 A2B43832C3D43833
A2B43832C3D43833 - Question 2 - Select One
A body takes twice the time to slides down a rough inclined plane at 45° to an identical smooth inclined plane. What is the coefficient of friction of rough plane?
A0.75B0.5C0.25D0.15 - Question 3 - Select One
A block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friction is μ)
A√2gl(μcosθ−sinθ)B√2gl(sinθ−μcosθ)C√2gl(sinθ+μcosθ)D√2gl(cosθ+μsinθ)

A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.View SolutionA smooth block is released from rest on a 45∘ inclined plane and it slides a distance 'd'. The time taken to slide is n times that on a smooth inclined plane. The coefficient of friction
View SolutionAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View Solution

