A rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
The volumetric stain
δVV=−PB
where P=ρgh
then−δVV=ρghB………..i
Since the volume of the sphere is V=4/3πr3, we have
δVV=3δrr……….ii
Using eqn i and ii we have
δr=ρgh3B
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.2
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.3
9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A spherical small ball of density ρ is gently released in a liquid of density σ(ρ>σ).The initial acceleration of the free fell of the ball will be
View SolutionA ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.
View Solution
Knowledge Check
A ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
Awith an increasing accelerationBwith a decreasing accelerationCwith a constant accelerationDwith zero accelerationWhen a rubber ball of volume v, bulk modulus K is at a depth h in water then decreases in its volume is
AhρgvKBhρgv2KChρgv3KDhρgv4KThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
A uniform ring of radius R and made up of a wire of cross - sectional radius r is rotated about its axis with a frequency f. If density of the wire is ρ and young's modulus is Y . Find the fractional change in radius of the ring .
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View Solution
A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
Find the force exerted by the liquid with density 2ρ on the ball
View SolutionAn object is taken to a depth of 2km inside an ocean. Percentage change in volume is 1.39%. Find bulk modulus
View Solution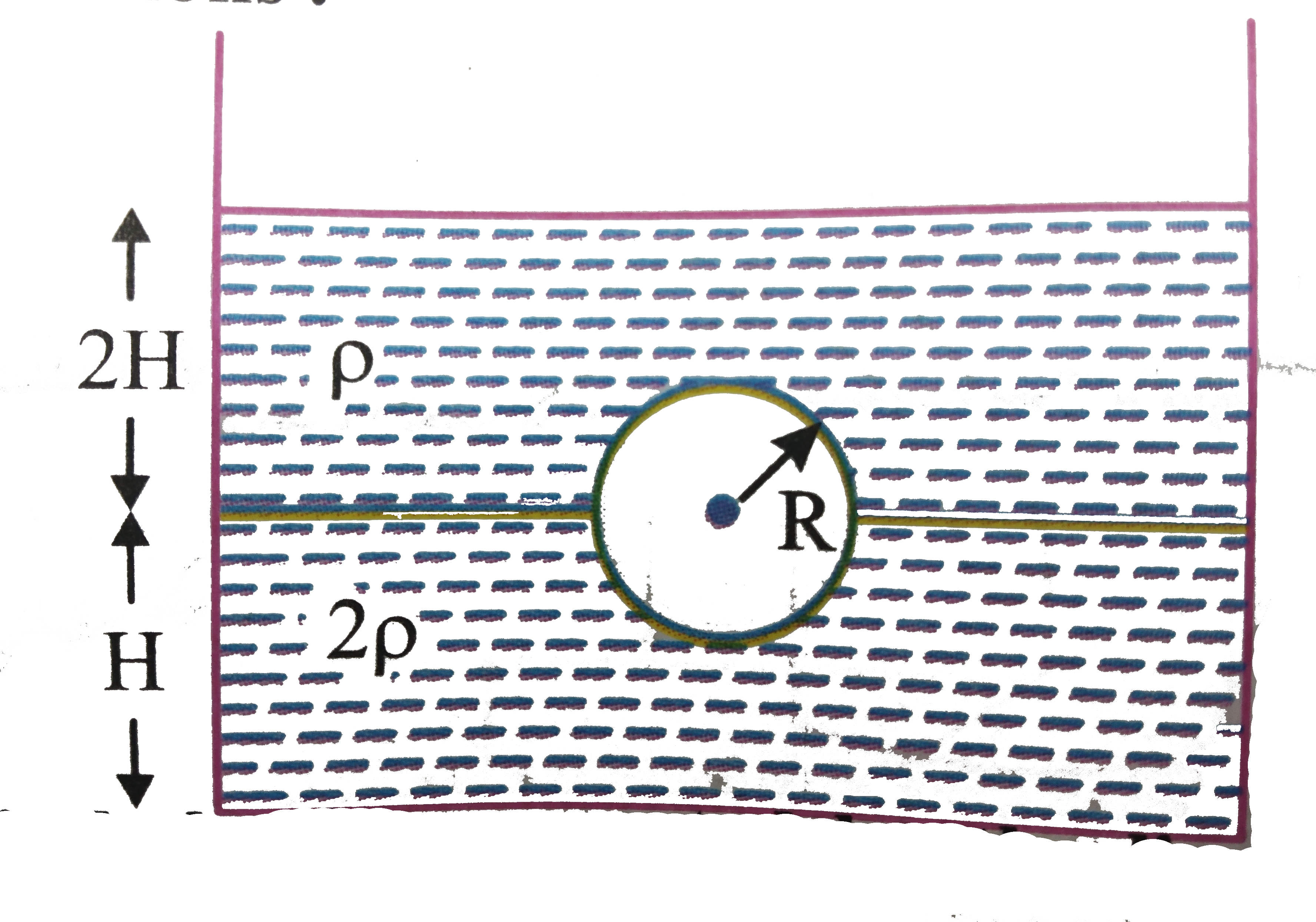
A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
If a hole is drilled at the bottom of the vessel then volume of the ball immersed inliquid with density ρ will
View Solution
