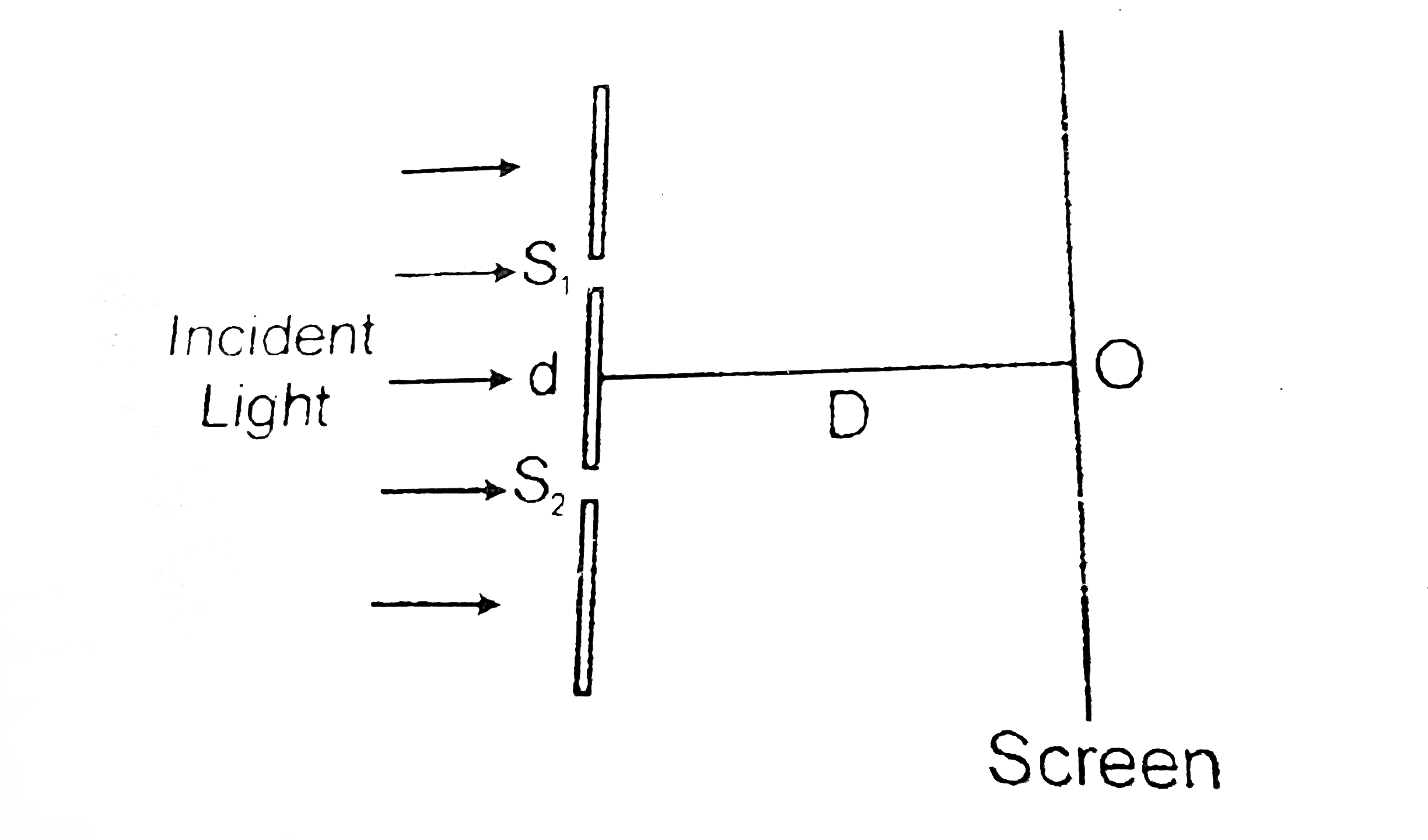
A screen is at distance D=80 cm form a diaphragm having two narrow slits S1 and S2 which are d=2 mm apart.
Slit S1 is covered by a transparent sheet of thickness
t1=2.5μm slit S2 is covered by another sheet of thickness
t2=1.25μm as shown if Fig. 2.52.
Both sheets are made of same material having refractive index μ=1.40
Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength λ=5000Å is incident normally on the diaphragm.
Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (μw=4/3)

Path difference at C.
Δx=t1(μ−1)−t2(μ−1)
μ(t1−t2)−(t1−t2)
(t1−t2(t1−(t2)
=(2.5−1.25)(1.4×34×101)=1.25×240=2.5400
⇒Δx=116μm
ϕ=2πλΔx=2π×45000×3×10−10×116×10−6=π3
Imax=4I0
Intensity at C, Ic=2I0(1+cos(π)3)=3I0
∴ Required raito =ICImax=34
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Solved Examples10videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.112videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
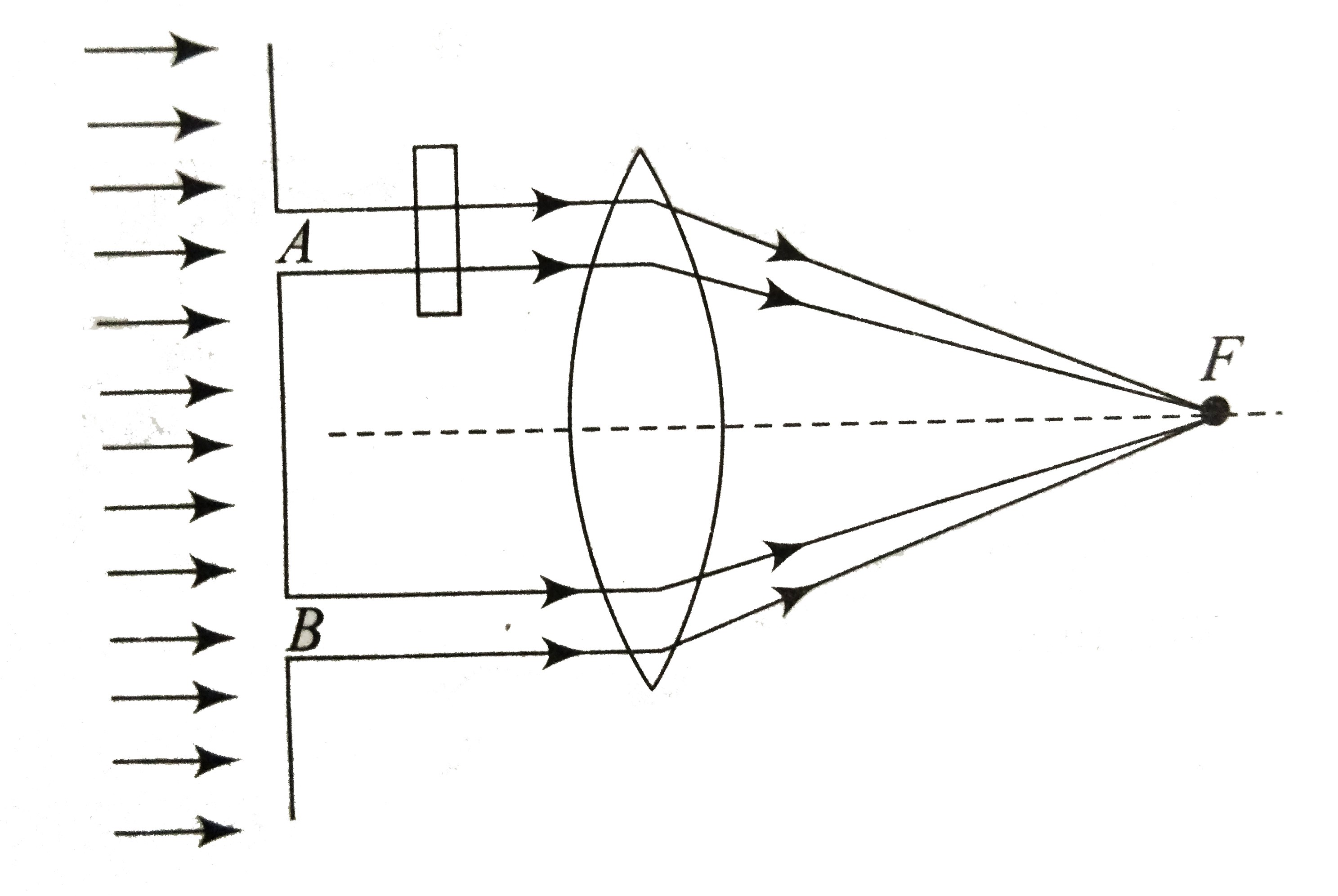 05:55View Solution
05:55View SolutionTwo coherent sources of light of intensity ratio β produce interference pattern. Prove that in the interferencepattern
Imax−IminImax+(Imin)=2√β1+β
where Imax and Imin are maximum and mininum intensities in the resultant wave.09:51View SolutionThree distinct current wires intersect a finite rectangular plane ABCD. The current is left wire and the loop is l1 . The direction of current in left most wire and righy most loop is downards as shown in the figure. The current l2through middle wire is adjusted so that the path integal of the total magnetic field along the perimeter of the rectangle is zero , that is ,∮ABCDA→B.d→s=0 then the current I2 is
 09:51View Solution
09:51View SolutionA screen is at distance D = 80 cm form a diaphragm having two narrow slits S_(1) and S_(2) which are d = 2 mm apart. Slit S_(1) is covered by a transparent sheet of thickness t_(1) = 2.5 mu m slit S_(2) is covered by another sheet of thikness t_(2) = 1.25 mu m as shown if Fig. 2.52. Both sheets are made of same material having refractive index mu = 1.40 Water is filled in the space between diaphragm and screen. Amondichromatic light beam of wavelength lambda = 5000 Å is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (mu_(w) = 4//3)
09:51View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
09:47View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
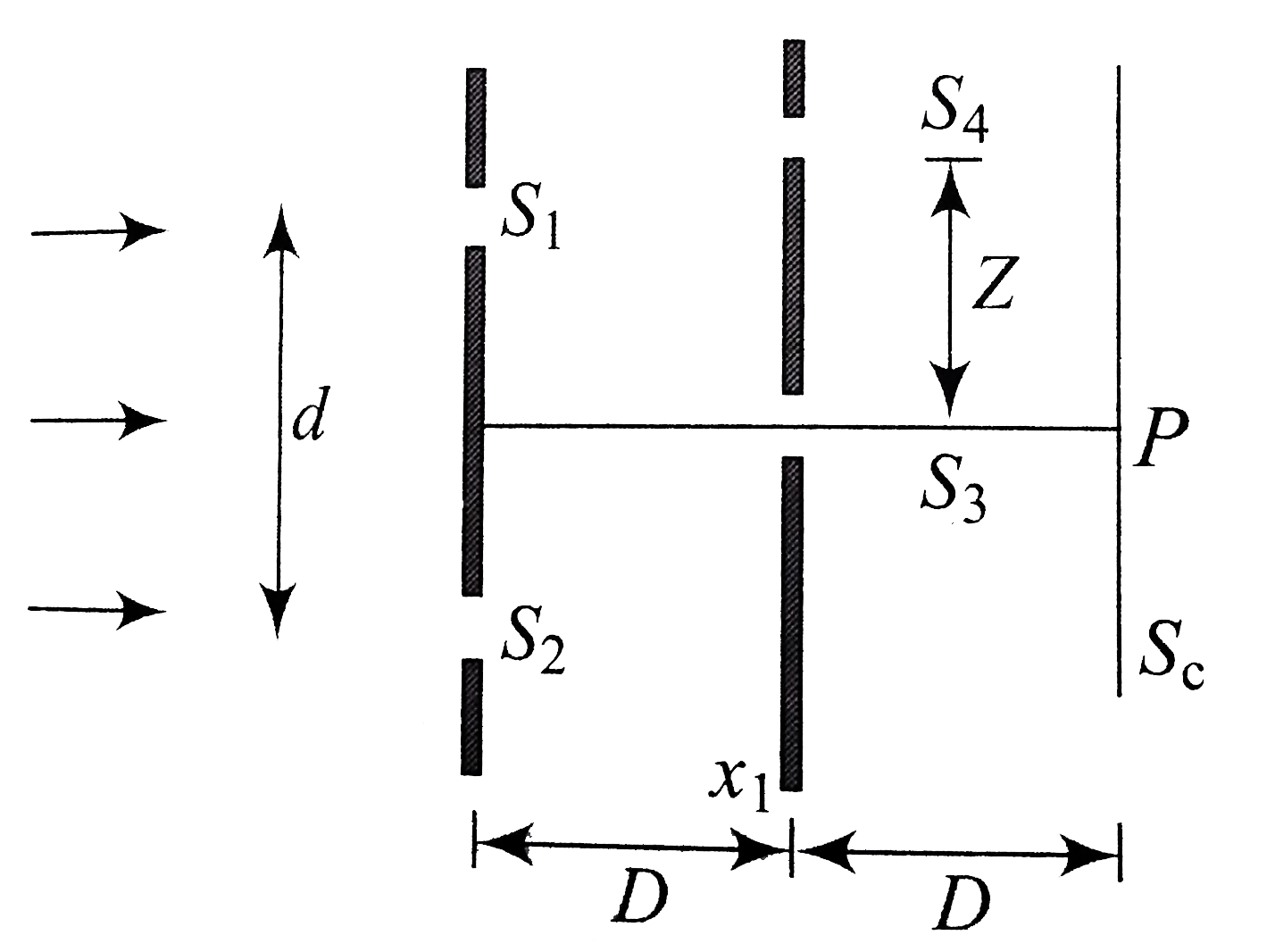
If z=λDd06:52View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
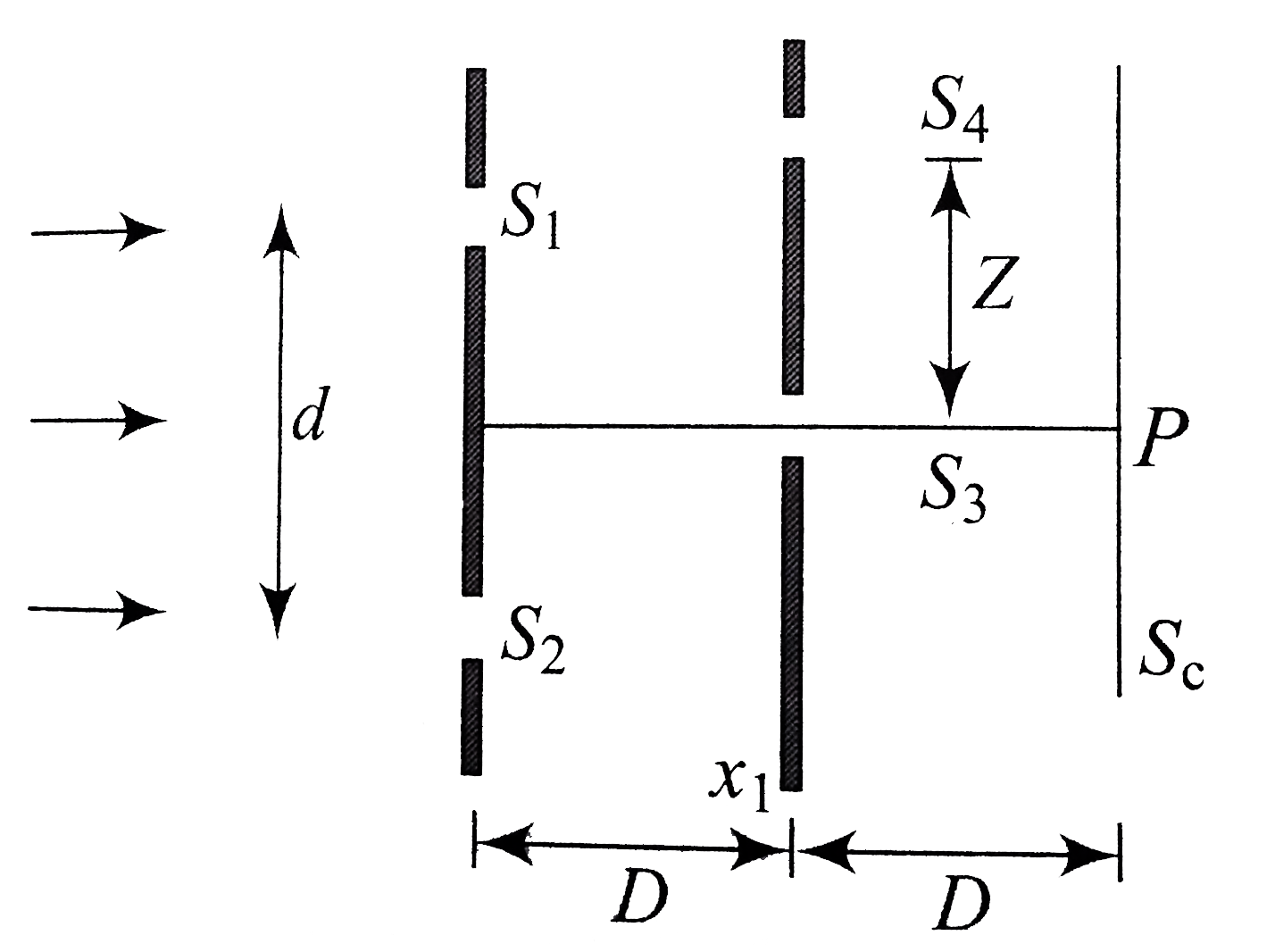
If z=λD4d05:06View SolutionIn a YDSE two him transparent sheet are used in front of the slits S_(1) & S_(2) having mu_(1)=1.6 and mu_(2)=1.4 respectively.If both sheets have thickness t ,the central maximum is observed at a distance of 5mm from center O .Now the sheets are replaced by another two sheets each of refractive index (mu_(1)-mu_(2))/(2) but having thickness t_(1)&t_(2)=(t_(1)-t_(2))/(2) .Now central maximum is observed at distance of 8mm from center O on the same side as before.Find the thickness t_(1) (in mu m) [Given:d=1mm,D=1m]
04:11View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
After placing the film of slit S1, the intensity at point O screen is :View SolutionTwo transparent sheets of thickness t1 and t2 and refractive indexes μ1 and μ2 are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

[D[(μ1−1)t1−(μ2−1)t2]d,(μ2−1)t2]07:58View SolutionTwo slits S_(1) and S_(2) illuminated by a white light source give a white central maxima. A transparent sheet of refractive index 1.25 and thickness t_(1) is placed in front of S_(1) . Another transparent sheet of refractive index 1.50 and thickness t_(2) is placed in front of S_(2) . If central maxima is not effected, then ratio of the thickness of the two sheets will be :
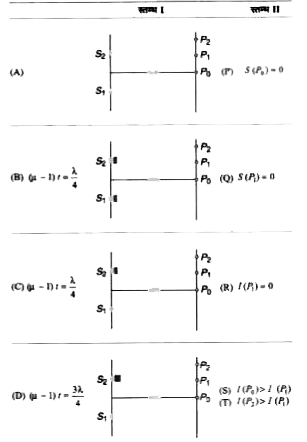
View SolutionColumn I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits S1 and S2 . In each of these cases S1P0=S2P0,S1P1−S2P1=λ/4 and S1P2−S2P2=λ/3, where λ is the wavelength of the light used. In the cases B,C and D, a transparent sheet of refractive index μ and thickness t is pasted on slit S1 . The thicknesses of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by δ(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation.
View Solutionस्तम्भ I में स्टैण्डर्ड यंग द्वि - स्लिट विन्यास की चार परिस्थितयाँ दिखाई गई है | जिनमें स्लिट S1 तथा S2 स्क्रीन से काफी दूरी पर है | प्रत्येक परिस्थिति में S1P0=S2P0,S1P1−S2P1=λ/4 और S1P2−S2P2=λ/3, जहाँ λ प्रकाश की तरंगदैर्ध्य है | B, C व D परिस्थितियों में स्लिट S1 के सामने μ अपवर्तनांक और t मोटाई की पारदर्शी शीट रखी गई है | इन सीटों की मोटाई प्रत्येक परिस्थिति में भिन्न - भिन्न है | स्क्रीन के किसी बिंदु P पर दोनों स्लिट से पहुँच रही प्रकाश तरंगों के फेज - अंतर को S( P ) से निरूपित किया गया है | तथा प्रकाश की तीव्रता को I ( P ) से निरूपित किया गया है | स्तम्भ I की प्रत्येक परिस्थितियों के लिए स्तम्भ II के प्रकथनों को आपस में मिलाइए |
 03:30View Solution
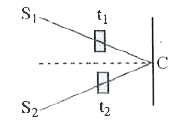
03:30View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
 04:12View Solution
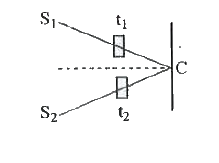
04:12View SolutionIn Young.s double slit experiment S1 andS2 are two slits. Films of thicknesses t1 and t2 refractive indices μ1andμ2 are placed in front ofS1andS2 repectively. If μ1t1=μ2t2 , then the central maximum will
 04:12View Solution
04:12View Solution

