A second harmonic has to be generated in a string of length l stretched between two rigid supports. The point where the string has to be plucked and touched are
Plucked at L4 and touch at L2
Plucked at L4 and touch at 3L2
Plucked at L2 and touch at L2
Plucked at L2 and touch at 3L4
The correct Answer is:A
To solve the problem of determining where to pluck and touch a string to generate the second harmonic, we can follow these steps:
Step 1: Understand the Harmonics of a String
The second harmonic of a string fixed at both ends has a specific pattern of nodes and antinodes. In the second harmonic, there are two segments of the wave, resulting in one node at the center and two antinodes at the ends.
Step 2: Identify the Nodes and Antinodes
For a string of length l:
- The nodes (points of no displacement) are located at:
- x=0 (left end)
- x=l2 (middle)
- x=l (right end)
- The antinodes (points of maximum displacement) are located at:
- x=l4
- x=3l4
Step 3: Determine the Plucking and Touching Points
- Plucking Point: This is where the string should be plucked to create an antinode. Therefore, the plucking points can be at:
- x=l4 or x=3l4
- Touching Point: This is where the string should be touched to create a node. The touching point can only be at:
- x=l2
Step 4: Conclusion
To generate the second harmonic in a string of length l:
- The string should be plucked at x=l4 or x=3l4.
- The string should be touched at x=l2.
Final Answer
- Plucking points: x=l4 and x=3l4
- Touching point: x=l2
---
The second harmonic of a string fixed at both ends has a specific pattern of nodes and antinodes. In the second harmonic, there are two segments of the wave, resulting in one node at the center and two antinodes at the ends.
For a string of length l:
- The nodes (points of no displacement) are located at:
- x=0 (left end)
- x=l2 (middle)
- x=l (right end)
- The antinodes (points of maximum displacement) are located at:
- x=l4
- x=3l4
- Plucking Point: This is where the string should be plucked to create an antinode. Therefore, the plucking points can be at:
- x=l4 or x=3l4
- x=l2
To generate the second harmonic in a string of length l:
- The string should be plucked at x=l4 or x=3l4.
- The string should be touched at x=l2.
- Plucking points: x=l4 and x=3l4
- Touching point: x=l2
Topper's Solved these Questions
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - HOTS
8 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - EXEMPLER
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason
15 Videos
Similar Questions
A string is vibrating in its fifth overtone between two rigid supports 2.4 m apart. The distance between successive node and antinode is
View SolutionTwo metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is L. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
View SolutionTwo strings A and B of equal lenth but un equal linear mass density are tied together with a knot and stretched between two supports. A particular frquency happens to produce a standing wave on each part, with node at the knot as shown. If linear mass density of the two strings A and B are μ1 and μ2 respectively, then

View Solution(a) A string of length L is stretched between two rigid supports. It is plucked at the centre. What type of wave is formed in it? What is its frequency?
(b) Obtain expressions for the frequency of higher harmonics of vibrations of a stretched string,
(c) State the laws of vibrating string-
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
View SolutionA rectangular plate of sides a and b is suspended from a ceiling by two parallel strings of length L each in the figure. The separation between the strings is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute harmonic motion. Find the time period.

View SolutionLength of a string tied to two rigid support is 40cm. Maximum length (wavelength in cm) of a stationary wave produced on it is
View Solution
Four identical metal butterflies are hanging from a light string of length 5l at equally placed points as shown. The ends of the string are attached to horizontal fixed support. The middle section of the string is horizontal . The relation between the angle θ1 and θ2 is given by
View Solution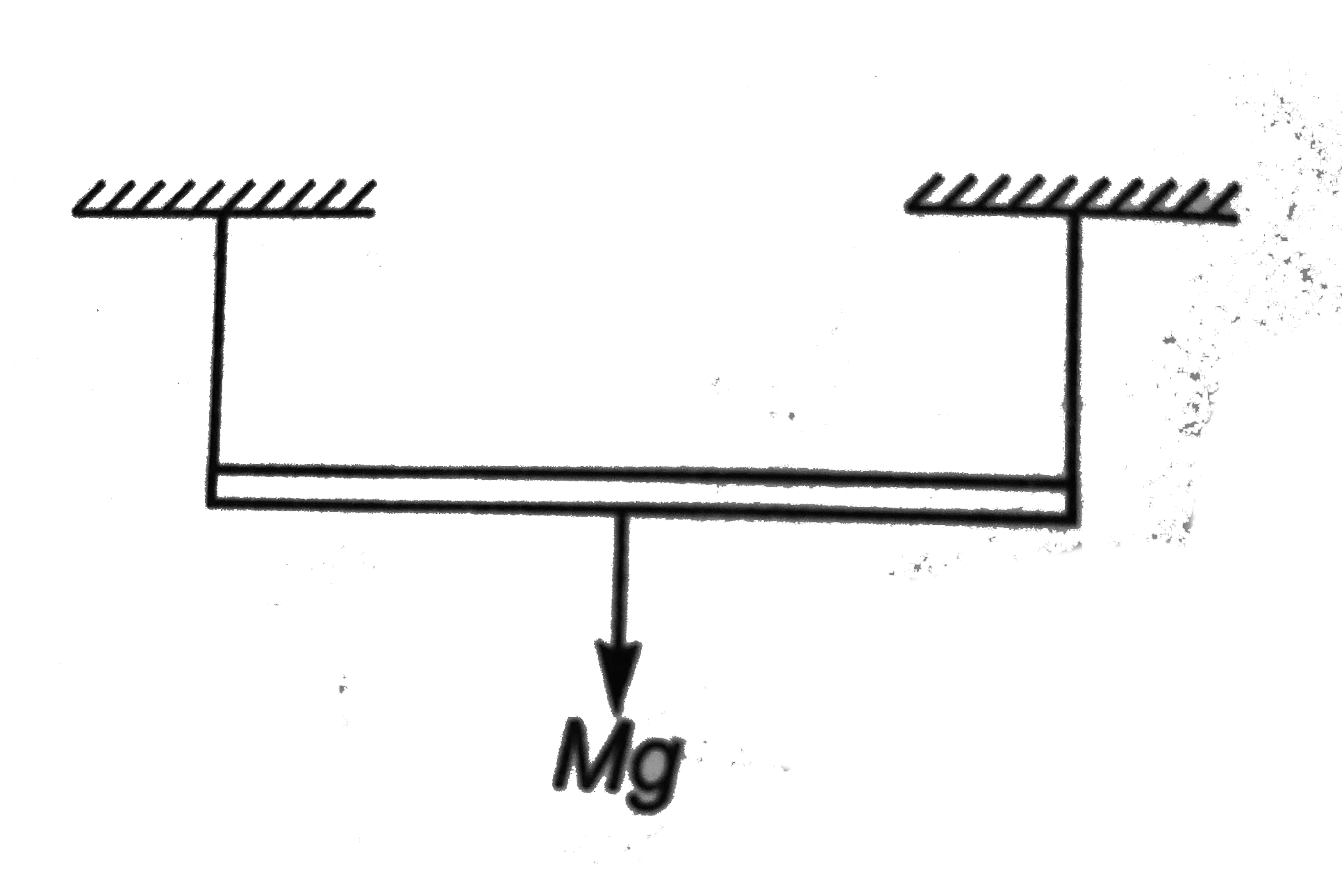
A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View Solution
