Two metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is L. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
tan−1[GMgL]
tan−1[GM2gL]
tan−1[GMgL2]
tan−1[2GMgL2]
The correct Answer is:C
To solve the problem step by step, we can break it down as follows:
Step 1: Understand the Setup
We have two metallic balls, each of mass m, suspended by strings of length L. The distance between the upper ends of the strings is also L. When the balls attract each other due to their mutual gravitational force, they will swing outwards and make an angle θ with the vertical.
Hint: Visualize the setup and the forces acting on the balls.
Step 2: Identify the Forces Acting on Each Ball
Each ball experiences:
- The gravitational force acting downwards, which is mg.
- The tension in the string, which acts along the string.
Hint: Draw a free-body diagram for one of the balls to identify the forces clearly.
Step 3: Analyze the Geometry
When the balls are displaced and make an angle θ with the vertical, we can analyze the geometry:
- The horizontal distance between the two balls can be represented as Lsin(θ).
- The vertical distance remains Lcos(θ).
Hint: Use trigonometric identities to relate the angle θ to the lengths involved.
Step 4: Apply Newton's Law of Gravitation
The gravitational force of attraction between the two balls can be expressed as:
\( F = \frac{G m^2}{r^2} \)
where r is the distance between the two balls. For small angles, we can approximate r as:
\( r \approx L \)
Hint: Remember that G is the universal gravitational constant.
Step 5: Set Up the Equilibrium Conditions
For the system to be in equilibrium:
- The vertical component of the tension must balance the weight of the ball:
\( T \cos(θ) = mg \)
- The horizontal component of the tension must balance the gravitational attraction:
\( T \sin(θ) = \frac{G m^2}{L^2} \)
Hint: Write down the equations for vertical and horizontal forces separately.
Step 6: Divide the Equations
Dividing the two equations gives:
\( \frac{T \sin(θ)}{T \cos(θ)} = \frac{\frac{G m^2}{L^2}}{mg} \)
This simplifies to:
\( \tan(θ) = \frac{G m}{g L^2} \)
Hint: This step involves manipulating the equations to isolate tan(θ).
Step 7: Solve for the Angle
To find the angle θ, we take the arctangent:
\( θ = \tan^{-1}\left(\frac{G m}{g L^2}\right) \)
Hint: Remember that g is the acceleration due to gravity, while G is the universal gravitational constant.
Final Answer
The angle at which the strings will be inclined with the vertical due to the attraction is:
\( θ = \tan^{-1}\left(\frac{G m}{g L^2}\right) \)
We have two metallic balls, each of mass m, suspended by strings of length L. The distance between the upper ends of the strings is also L. When the balls attract each other due to their mutual gravitational force, they will swing outwards and make an angle θ with the vertical.
Each ball experiences:
- The gravitational force acting downwards, which is mg.
- The tension in the string, which acts along the string.
When the balls are displaced and make an angle θ with the vertical, we can analyze the geometry:
- The horizontal distance between the two balls can be represented as Lsin(θ).
- The vertical distance remains Lcos(θ).
The gravitational force of attraction between the two balls can be expressed as:
\( F = \frac{G m^2}{r^2} \)
where r is the distance between the two balls. For small angles, we can approximate r as:
\( r \approx L \)
For the system to be in equilibrium:
- The vertical component of the tension must balance the weight of the ball:
\( T \cos(θ) = mg \)
- The horizontal component of the tension must balance the gravitational attraction:
\( T \sin(θ) = \frac{G m^2}{L^2} \)
Dividing the two equations gives:
\( \frac{T \sin(θ)}{T \cos(θ)} = \frac{\frac{G m^2}{L^2}}{mg} \)
This simplifies to:
\( \tan(θ) = \frac{G m}{g L^2} \)
To find the angle θ, we take the arctangent:
\( θ = \tan^{-1}\left(\frac{G m}{g L^2}\right) \)
The angle at which the strings will be inclined with the vertical due to the attraction is:
\( θ = \tan^{-1}\left(\frac{G m}{g L^2}\right) \)
Similar Questions
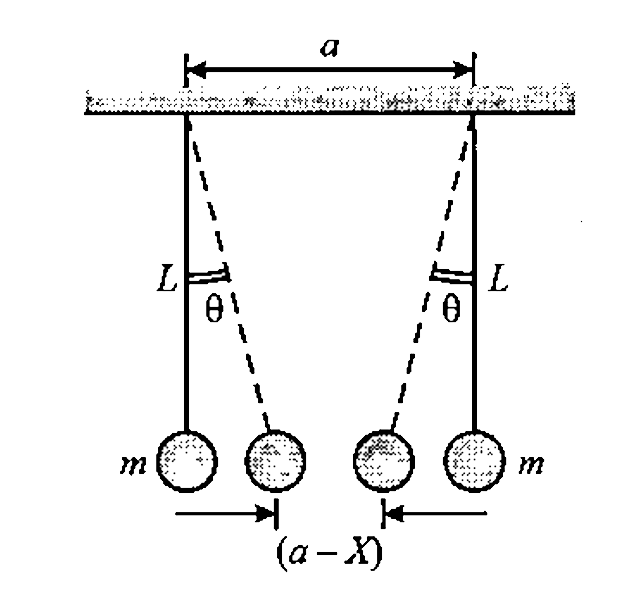
Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle thit θ with the vertical. Find the work done by the force F
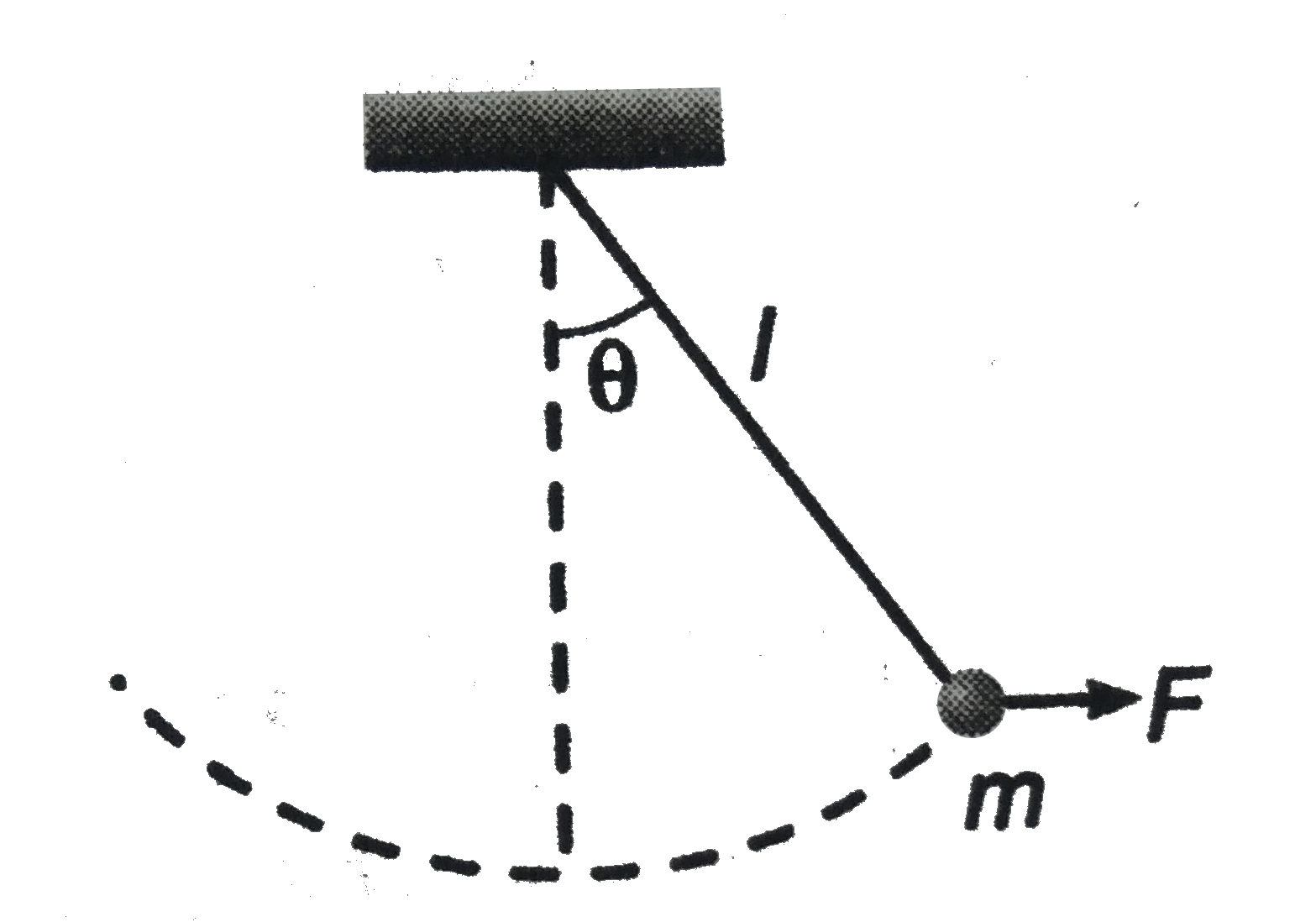 .
.
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F
 .
.
View SolutionA block of mass 10kg is suspended from string of length 4m. When pulled by a force F along horizontal from midpoint. Upper half of string makes 45∘ with vertical, value of F is
View SolutionA mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
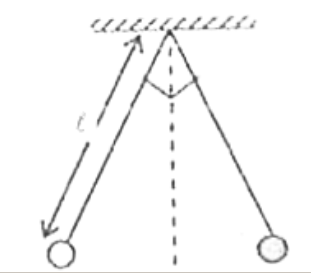
View SolutionTwo small metallic spheres each of mass 'm' are suspended together with strings of length 'l' and placed together. When a quantum of charge 'q' is transferred to each the strings make and angle of 90∘ with each other. The value of 'q' is
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution
