A semicircular wire hs a length L and mass M. A paricle of mass m is placed at the centre of the circle. Find the gravitational attrction on the particle due to the wire.
The correct Answer is:B
To find the gravitational attraction on a particle of mass m placed at the center of a semicircular wire of length L and mass M, we can follow these steps:
Step 1: Understand the Geometry
The semicircular wire has a radius R and a length L. The relationship between the length of the semicircle and the radius is given by:
L=πR
From this, we can express the radius as:
R=Lπ
Step 2: Divide the Wire into Differential Elements
Consider a small element of the wire dθ at an angle θ from the vertical. The length of this small element dx can be expressed as:
dx=Rdθ
The mass dM of this small element can be calculated using the mass per unit length:
dM=MLdx=MLRdθ
Step 3: Calculate the Gravitational Force from a Differential Element
The gravitational force dF exerted by the small mass dM on the mass m at the center is given by Newton's law of gravitation:
dF=G⋅dM⋅mR2
Substituting for dM:
dF=G⋅(MLRdθ)⋅mR2=G⋅M⋅mL⋅Rdθ
Step 4: Resolve the Force into Components
The gravitational force dF acts along the line connecting the mass m and the element dM. We can resolve dF into two components: one along the vertical direction (which contributes to the net force) and one along the horizontal direction (which cancels out due to symmetry). The vertical component is:
dFy=dF⋅sin(θ)=G⋅M⋅mL⋅Rdθ⋅sin(θ)
Step 5: Integrate Over the Semicircle
To find the total gravitational force F acting on the mass m, we need to integrate dFy from θ=0 to θ=π2 and then multiply by 2 (to account for the symmetry of the semicircle):
F=2∫π20G⋅M⋅mL⋅Rsin(θ)dθ
Step 6: Solve the Integral
The integral of sin(θ) is:
∫sin(θ)dθ=−cos(θ)
Evaluating the integral:
∫π20sin(θ)dθ=(−cos(θ))π20=−cos(π2)+cos(0)=0+1=1
Thus, the total force becomes:
F=2⋅G⋅M⋅mL⋅R⋅1=2G⋅M⋅mL⋅R
Step 7: Substitute for Radius
Now, substituting R=Lπ:
F=2G⋅M⋅mL⋅Lπ=2G⋅M⋅m⋅πL2
Final Answer
The gravitational attraction on the particle due to the wire is:
F=2G⋅M⋅m⋅πL2
The semicircular wire has a radius R and a length L. The relationship between the length of the semicircle and the radius is given by:
L=πR
From this, we can express the radius as:
R=Lπ
Consider a small element of the wire dθ at an angle θ from the vertical. The length of this small element dx can be expressed as:
dx=Rdθ
The mass dM of this small element can be calculated using the mass per unit length:
dM=MLdx=MLRdθ
The gravitational force dF exerted by the small mass dM on the mass m at the center is given by Newton's law of gravitation:
dF=G⋅dM⋅mR2
Substituting for dM:
dF=G⋅(MLRdθ)⋅mR2=G⋅M⋅mL⋅Rdθ
The gravitational force dF acts along the line connecting the mass m and the element dM. We can resolve dF into two components: one along the vertical direction (which contributes to the net force) and one along the horizontal direction (which cancels out due to symmetry). The vertical component is:
dFy=dF⋅sin(θ)=G⋅M⋅mL⋅Rdθ⋅sin(θ)
To find the total gravitational force F acting on the mass m, we need to integrate dFy from θ=0 to θ=π2 and then multiply by 2 (to account for the symmetry of the semicircle):
F=2∫π20G⋅M⋅mL⋅Rsin(θ)dθ
The integral of sin(θ) is:
∫sin(θ)dθ=−cos(θ)
Evaluating the integral:
∫π20sin(θ)dθ=(−cos(θ))π20=−cos(π2)+cos(0)=0+1=1
Thus, the total force becomes:
F=2⋅G⋅M⋅mL⋅R⋅1=2G⋅M⋅mL⋅R
Now, substituting R=Lπ:
F=2G⋅M⋅mL⋅Lπ=2G⋅M⋅m⋅πL2
The gravitational attraction on the particle due to the wire is:
F=2G⋅M⋅m⋅πL2
Topper's Solved these Questions
Similar Questions
(a) A uniform rod of mass M and length L is placed at distance L from a point mass m as shown. Find force on m
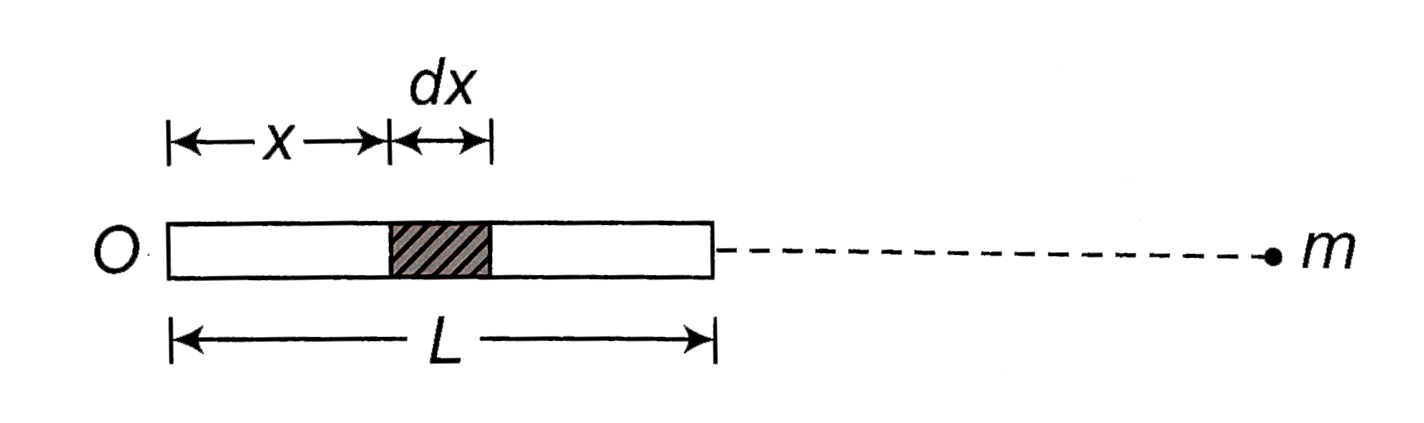
(b) A semiconductor wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. find the gravitational attraction on the particle due to the wire.
View SolutionEight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
 .
.
View Solution
Knowledge Check
A body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
A−GH(M+m)B−GH(M−m)C−GH(mMM+m)D−GH(mMM−m)Six particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
A6Gm2a2B6Gmm0a2CzeroD6Gma4Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−2√2GmlB−3√2GmlC−2GmlD−4√2Gml
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
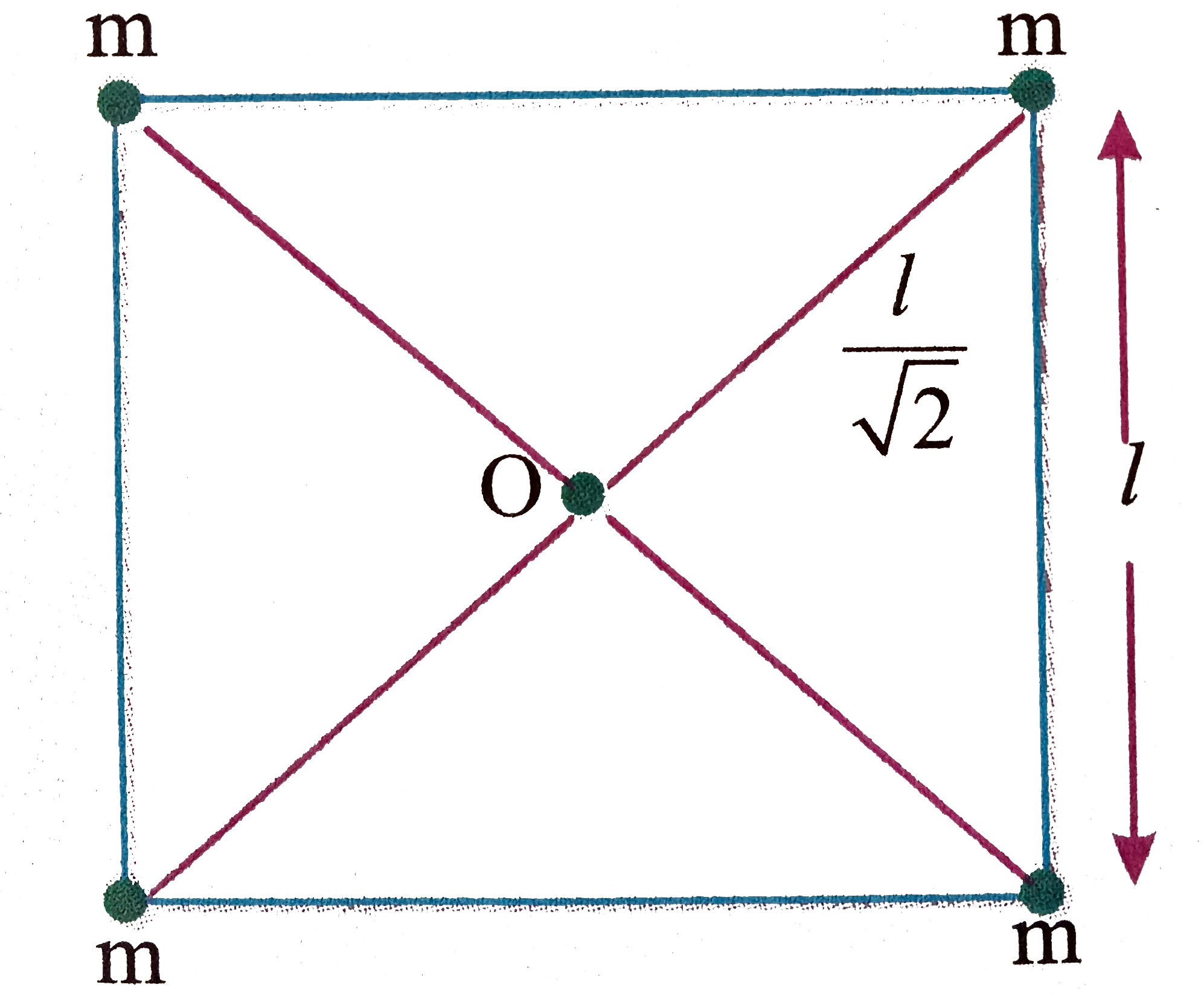
View Solution
