A set of a identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surface of any two adjacent blocks is L. The block at one and is given a speed v towards the next one at time t=0. All collisiona are completely inelastic , then the last block starts moving at
(n−1)Lv
n(n−1)L2v
(n+1)Lv
n(n+1)L2v
The correct Answer is:B

Since collision is perfectly inelasticso all the blocks will stick together one by one and move in a form of combined mass.
Time required to cover a displace 'L' by first block =Lv
Now first and second block will stick together and move with v/2 velocity (by applying conservation of momentum) and combined system will take time
Lv/2=2Lv to reach up to block third.
Now these three will move with velocity v/3 and combined system will take time Lv/3=3Lv to reach upto the block fourth.
So, total time
=Lv+2Lv+3Lv+....(n−1)Lv=n(n−1)L2v
Topper's Solved these Questions
Similar Questions
Two blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

View Solution2n identical cubical blocks are kept in a straight line on a horizontal smooth surface. The separation between any two consecutive blocks is same. The odd numbered blocks 1,3,5,.....(2n–1) are given velocity v to the right whereas blocks 2,4,6,......2n are given velocity v to the left. All collisions between blocks are perfectly elastic. Calculate the total number of collisions that will take place.

View Solution
Knowledge Check
A set of n identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surfaces of any two adjacent blocks is L . The block at one end is given a speed v towards the next one at time 0 t . All collisions are completely inelastic, then
AThe last block starts moving at t=(n−1)LvBThe last block starts moving at t=n(n−1)L2vCthe centre of mass of the system will have a final speed vDThe centre of mass of the system will have a final speed vn.Two blocks A and B are placed one over the other on a smooth horizontal surface. The maximum horizontal force that can be applied on the lower block A, so that A and B move without separation is 49N. The coefficient of friction between A and B is (take g = 9.8ms−2 )
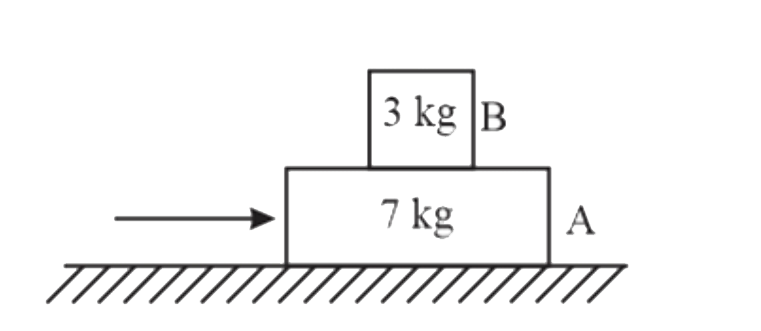 A0.2B0.3C0.5D0.8
A0.2B0.3C0.5D0.8Two identical 5kg blocks are moving with same speed of 2m/s towards each other along a frictionless horizontal surface . The two blocks collide , stick together and come to rest. Consider the two blocks as a system . The work done by the external and ijnternal force are respectively:
A0,0B0,20JC0,−20JD21J,−20J
Figure shows four blocks that are being pulled along a smooth horizontal surface.The masses of the blocks and tension in one cord are given.The pulling force F is
View SolutionA large number of small identical blocks, each of mass m, are placed on a smooth horizontal surface with distance between two successive blocks being d. A constant force F is applied on the first block as shown in the figure
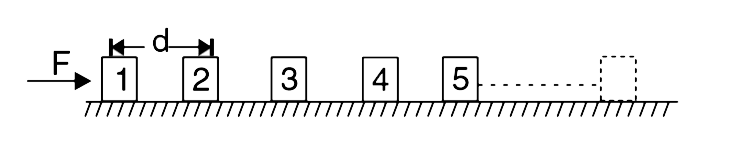
(a) If the collisions are elastic, plot the variation of speed of block 1 with time.
(b) Assuming the collisions to be perfectly inelastic, find the speed of the moving blocks after n collisions. To what value does this speed tend to if n is very large.
View SolutionConsider a large block placed on a smooth horizontal surface, with a man standing at one end of the block. The man walks to the other end, relative to the block. The distances (absolute) moved by the man and the block are :
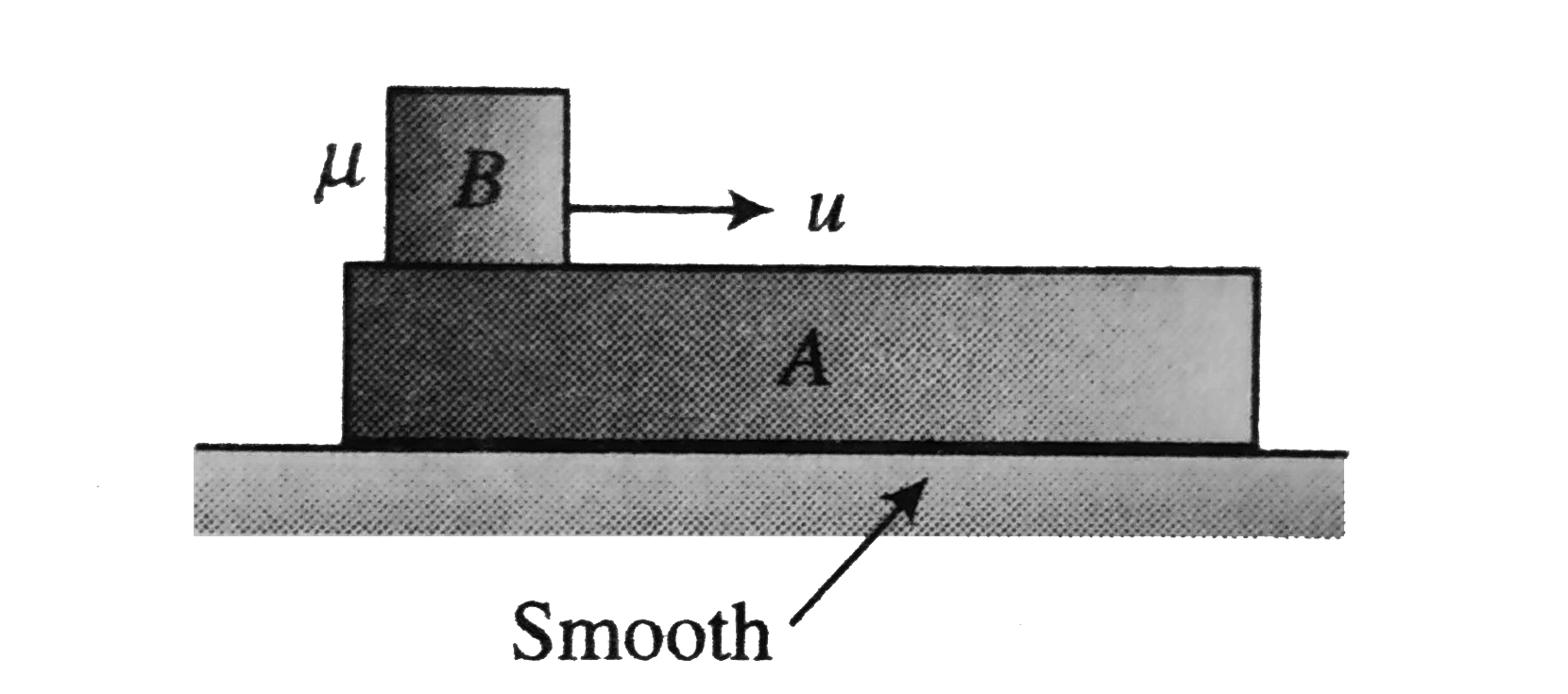
View SolutionA long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View Solution
