(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by:
$({\vec{E}}_{2} - {\vec{E}}_{1}) . \hat{n} = \frac{σ}{ε_{0}}$
where $\hat{n}$ is a unit vector normal to the surface of a point and $σ$ is the surface charge density at that point. (The direction of $\hat{n}$ is from side 1 to side 2). Hence, show that just outside a conductor, the electric field is $\frac{σ \hat{n}}{ε_{0}}$ .
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.

Text Solution

Verified by Experts

(a) The electric field due to a charged surface having surface charge density $σ$ is given by:
$\vec{E} = \frac{σ}{2 ε_{0}} \hat{n}$
Let us consider a charged surface carrying surface charge density $σ$ as shown in the figure.

The electric field intensity at the side-2 is given by:
${\vec{E}}_{2} = \frac{σ}{2 ε_{0}} \hat{n}$
The electric field intensity at side-1 is given by:
${\vec{E}}_{1} = \frac{σ}{2 ε_{0}} \hat{n}$
There will be discontinuity in the electric field due the charged surface as the directions of the ${\vec{E}}_{1} and {\vec{E}}_{2}$ will be opposite.
Thus, the discontinuity in the electric field is given by,
${\vec{E}}_{2} - {\vec{E}}_{1} = \frac{σ}{2 ε_{0}} \hat{n} - (- \frac{σ}{2 ε_{0}}) \hat{n} = \frac{σ}{ε_{0}} \hat{n}$
$\Rightarrow ({\vec{E}}_{2} - {\vec{E}}_{1}) \hat{n} = (\frac{σ}{ε_{0}} \hat{n}) \hat{n} = \frac{σ}{ε_{0}}$
Since the difference of the electric field intensities on the two sides of the surface is non-zero, the two electric fields are unequal. So, there is a discontinuity.
In case of the surface is conducting the electric field will be zero at its one side because that lies inside the conductor.s volume. Thus, on substituting ${\vec{E}}_{1} = 0$
${\vec{E}}_{2} - {\vec{E}}_{1} = \frac{σ}{ε_{0}} \hat{n}$
${\vec{E}}_{2} = \frac{σ}{ε_{0}} \hat{n}$
(b)
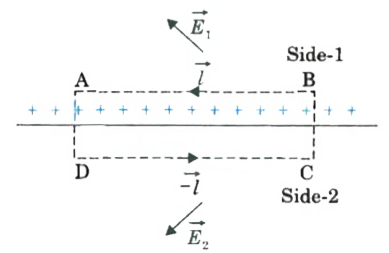
Let ${\vec{E}}_{1} and {\vec{E}}_{2}$ be the electric fields on both sides of the charged surface.
Let us assume a rectangular loop of negligible width and length $l$ as shown in above figure. Side AB of the loop is on side-1 of the charged surface and the side CD is on the side-2 of the charged surface.
As we know the net work done in moving a charged particle in a closed loop is zero inside electrostatic field.
Thus, work done in moving a unit charged particle along ABCD must be zero.
${\vec{E}}_{1} \cdot \vec{l} + {\vec{E}}_{2} . (- \vec{l}) = 0$
[The width of the loop AD and BC is neglected]
Thus, $E_{1} l {\cos θ}_{1} - E_{2} l {\cos θ}_{2} = 0$
$\Rightarrow E_{1} {\cos θ}_{1} = E_{2} {\cos θ}_{2}$
Here, $θ_{1} and θ_{2}$ are the angles made by ${\vec{E}}_{1}$ and ${\vec{E}}_{2}$ with the charged surface. $E_{1} {\cos θ}_{1} and E_{2} {\cos θ}_{2}$ are the tangential components of the electric field on two sides of the surface and we have proved them to be equal. Hence, the tangential component of electric field (if it exists) will be same on both sides.

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

MODERN PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE -NCERT FILE Solved (Additional Exercises)

Home
Ask Doubt
Profile