A simple pendulum executes S.H.M. in water with a time period Tw. When the bob executes S.H.M. in air, time period is Ta, IF the density of bob of simple pendulum is 5000/3 kg/m3 and frictional force of water is neglected, then find the relation between TwandTa.
To find the relation between the time periods Tw (time period in water) and Ta (time period in air) for a simple pendulum, we need to consider the effective acceleration due to gravity in both mediums.
1. Understanding the Time Period Formula:
The time period T of a simple pendulum is given by the formula:
T=2π√Lgeffective
where L is the length of the pendulum and geffective is the effective acceleration due to gravity.
2. Effective Gravity in Air:
In air, the only force acting on the bob is its weight. Therefore, the effective acceleration due to gravity geffective, air is simply:
geffective, air=g
where g is the acceleration due to gravity.
3. Effective Gravity in Water:
When the pendulum bob is submerged in water, it experiences two forces: its weight mg acting downwards and the buoyant force Fb acting upwards. The buoyant force can be calculated as:
Fb=ρw⋅V⋅g
where ρw is the density of water, V is the volume of the bob, and g is the acceleration due to gravity.
The net downward force on the bob when submerged is:
Fnet=mg−Fb=mg−ρw⋅V⋅g
The effective acceleration due to gravity in water geffective, water is given by:
geffective, water=Fnetm=mg−ρw⋅V⋅gm
Since the mass m can be expressed in terms of the density of the bob ρb and its volume V:
m=ρb⋅V
Substituting this into the equation gives:
geffective, water=g−ρw⋅gρb
4. Relating the Time Periods:
Now we can write the time periods in both cases:
- In air:
Ta=2π√Lg
- In water:
Tw=2π
⎷Lg−ρw⋅gρb
5. Finding the Ratio:
To find the relation between Tw and Ta, we take the ratio:
TwTa=√g√g−ρw⋅gρb
Simplifying this gives:
TwTa=√gg−ρwρb⋅g=√ρbρb−ρw
6. Substituting Values:
Given that the density of the bob ρb=50003kg/m3 and the density of water ρw=1000kg/m3:
TwTa=
⎷5000350003−1000=
⎷500035000−30003=√50002000=√52
7. Final Relation:
Therefore, we can express Tw in terms of Ta:
Tw=Ta⋅√52
Final Answer:
Tw=Ta⋅√52
The time period T of a simple pendulum is given by the formula:
T=2π√Lgeffective
where L is the length of the pendulum and geffective is the effective acceleration due to gravity.
In air, the only force acting on the bob is its weight. Therefore, the effective acceleration due to gravity geffective, air is simply:
geffective, air=g
where g is the acceleration due to gravity.
When the pendulum bob is submerged in water, it experiences two forces: its weight mg acting downwards and the buoyant force Fb acting upwards. The buoyant force can be calculated as:
Fb=ρw⋅V⋅g
where ρw is the density of water, V is the volume of the bob, and g is the acceleration due to gravity.
Fnet=mg−Fb=mg−ρw⋅V⋅g
The effective acceleration due to gravity in water geffective, water is given by:
geffective, water=Fnetm=mg−ρw⋅V⋅gm
Since the mass m can be expressed in terms of the density of the bob ρb and its volume V:
m=ρb⋅V
Substituting this into the equation gives:
geffective, water=g−ρw⋅gρb
Now we can write the time periods in both cases:
- In air:
Ta=2π√Lg
- In water:
Tw=2π
⎷Lg−ρw⋅gρb
To find the relation between Tw and Ta, we take the ratio:
TwTa=√g√g−ρw⋅gρb
Simplifying this gives:
TwTa=√gg−ρwρb⋅g=√ρbρb−ρw
Given that the density of the bob ρb=50003kg/m3 and the density of water ρw=1000kg/m3:
TwTa=
⎷5000350003−1000=
⎷500035000−30003=√50002000=√52
Therefore, we can express Tw in terms of Ta:
Tw=Ta⋅√52
Tw=Ta⋅√52
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT FILE (Textbook Exercises)
19 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT (Additional Exercises)
6 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Conceptual Questions
18 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
The bob of simple pendulum executes SHM in water with a period T, while the period of oscillation of the bob is T0 in air. Neglecting frictional force of water and given that the density of the bob is 40003kgm−3 , find the ration between T and T0.
View SolutionA simple pendulum is executing simple harmonic motion with a time period T. If the length of the pendulum is increased by 21%, the percentage increase in the time period of the pendulum of is
View Solution
Knowledge Check
A simple pendulum executing S.H.M. is falling freely along with the support. Then
AIts periodic time decreasesBIts periodic time increasesCIt does not oscillate at allDNone of theseA simple pendulum oscillates in air with time period T and amplitude A . As the time passes
AT and A both decreaseBT increases and A is constantCT increases and A decreasesDT decrases and A is constantThe graph between time period (T) and length (l) of a simple pendulum is
A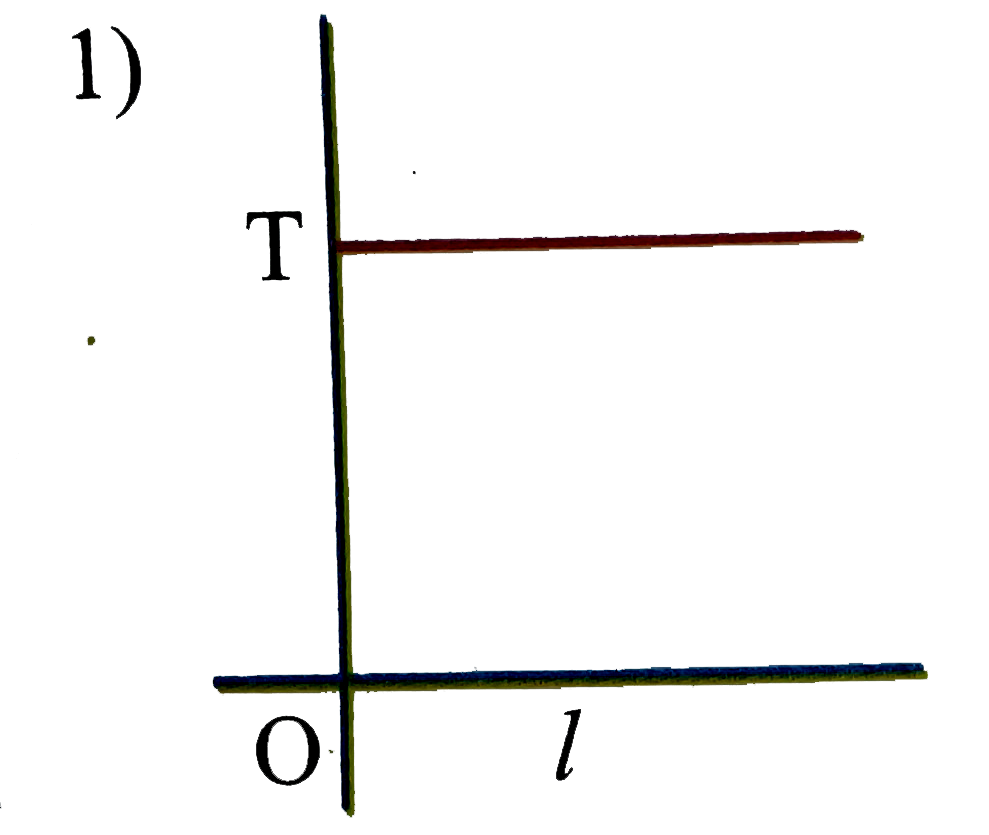 B
B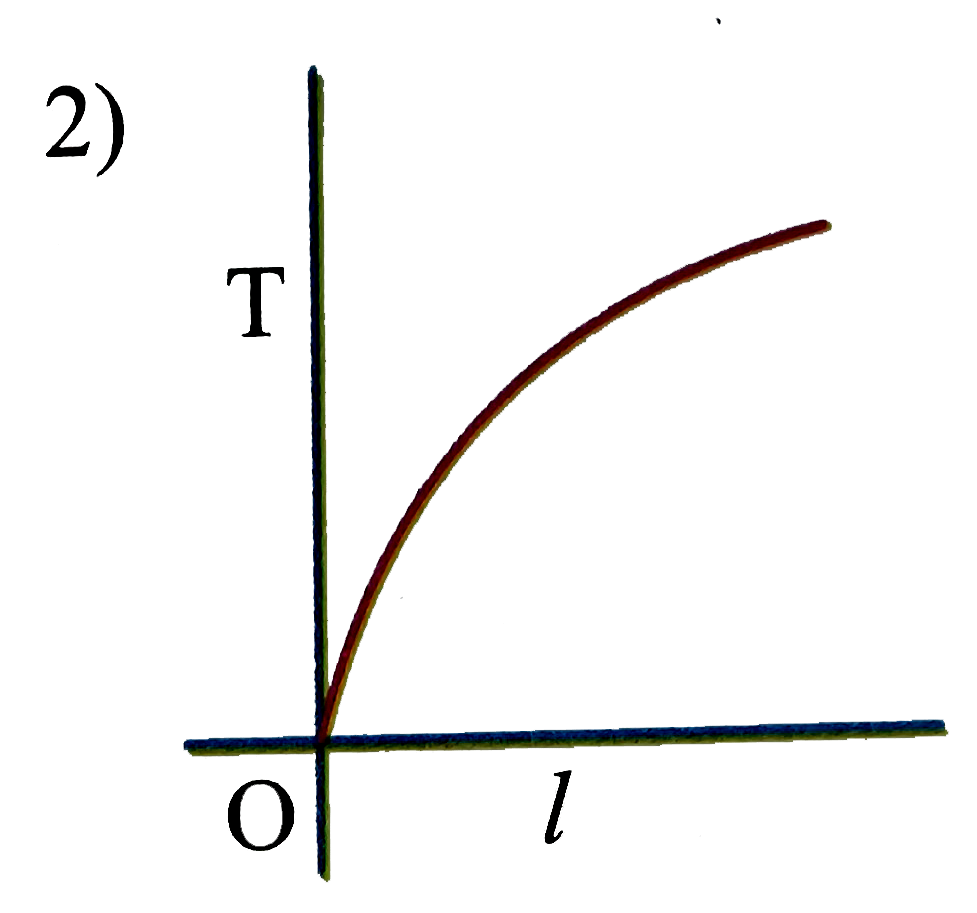 C
C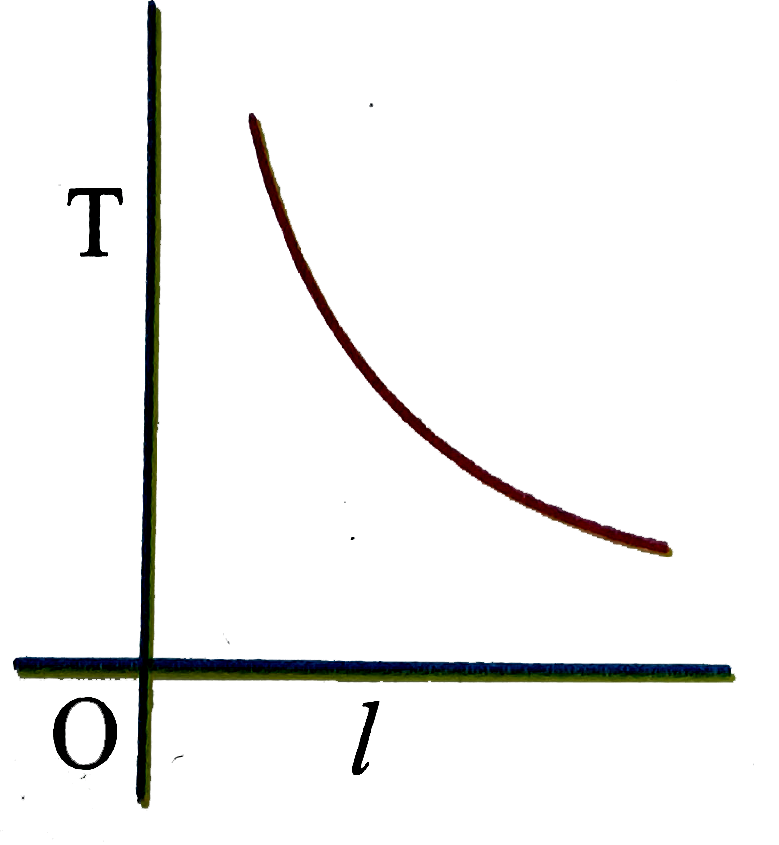 D
D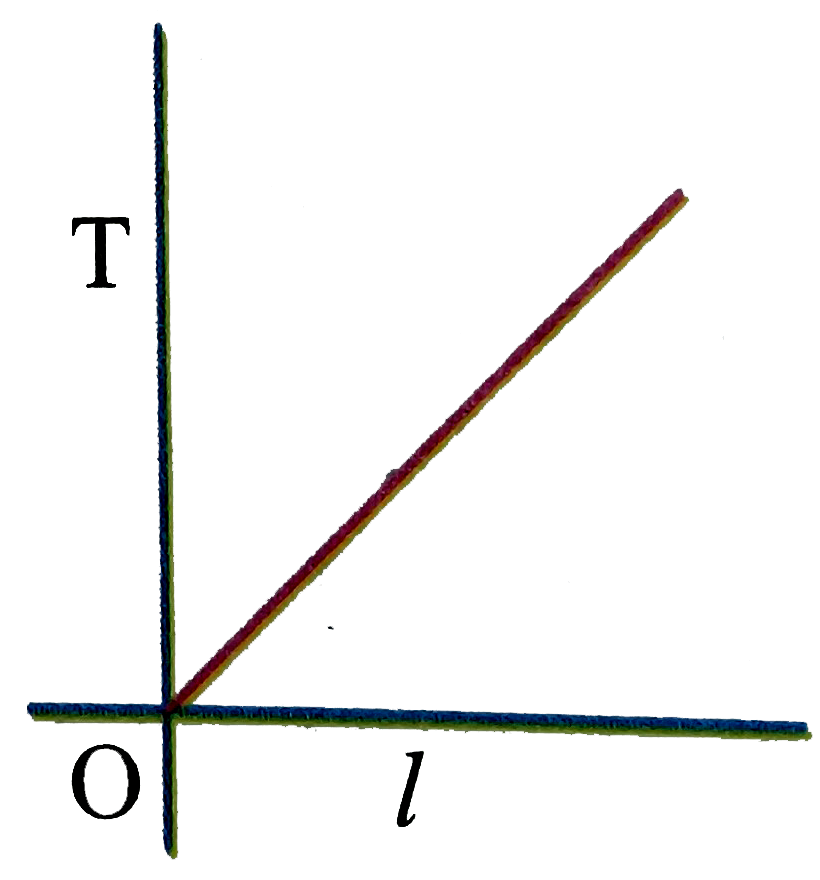
The graph of time period (T) of a simple pendulum versus its length (I) is
View SolutionA simple pendulum performs SHM about x=0 an amplitude a and time period T. the speed of pendulum at x=a2 will be
View SolutionA simple pendulum performs SHM about x=0 an amplitude a and time period T. The speed of pendulum at x=a2 will be
View SolutionThe bob of a simple pendulum executm simple harmonic motion in water with a period t, while the period of oscillation of the bob is t0 in air. Negleting frictional force of water and given that the density of the bob is (4//3)xx1000 kg//m^(3).
What relationship between t and t0 is true.
View SolutionFor a simple pendulum, the graph between T2andL (where T is the time period & Lis the length) is
View Solution
