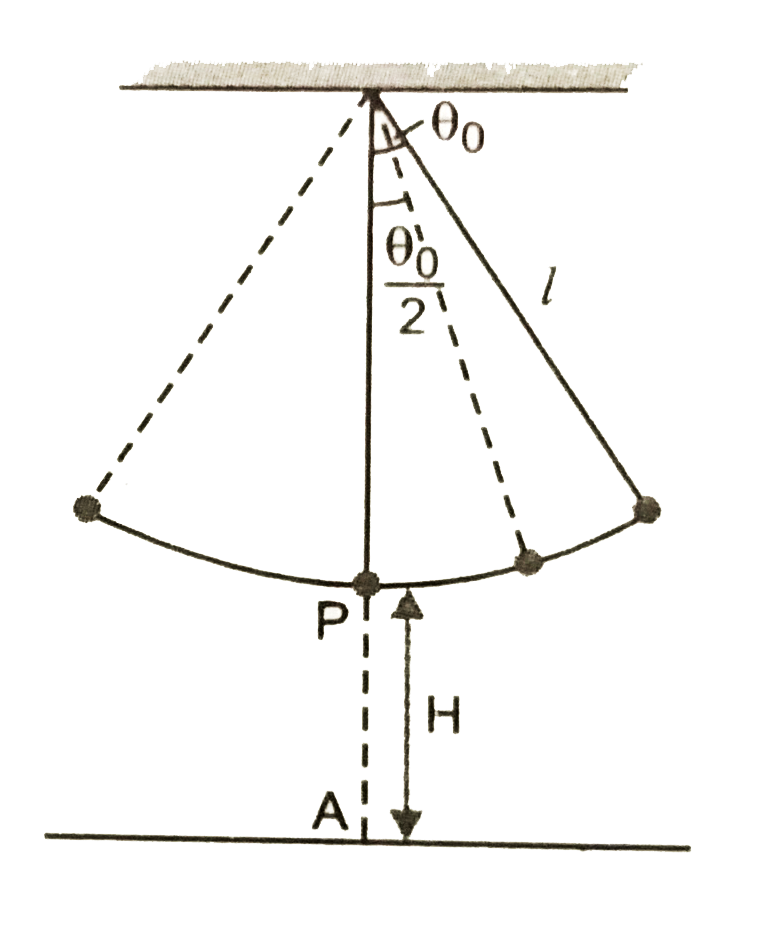
A simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is θ0 the string snaps at 0=θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θ0 to be small, so that sinθ0≈θ0andcosθ0≈1.

Here, θ0 is the angular amplitude of simple pendulum and time period, T=1s. The angular displacement of the bob of the pendulum at any inisant t is given by
θ=θ0sinωt=θ0sin(2πT)t
=θ0sin(2π1)t=θ0sin2πt ..(i)
(∵T=1s.)
At time t1, let θ=θ0/2 then from (i), we have
θ02=θ0sin2πt1 or 2πt1=π6ort1=112s
Differentiating (i) w.r.t. t, we have
dθdt=2πθ0cos2πt
When t=t1=112, then dθdt=2πthet0cos2π×112=2πθ0×√32=√3πθ0
Angular velocity of the bob of simple pendulum is ω=dθdt=√3πθ0
velocity of the bob of simple pendulum, v=rω=lω=l(√3πθ0)
It is acting perpendicular to string.
The vertical component velocity of bob, vy=vsin(θ0/2)=l√3πθ0sin(θ0/2)
Horizontal component velocity of bob, vx=vcos(θ0/2)=l√3πθ0cos(θ0/2)
The height of the bob when the pendulum snaps is , H′+H+lcos(θ0/2)=H+l[1−cos(θ0/2)]
If t' is the time taken by the bob to fall through height H(') , then using the relation , S=ut+12at2,
we have s=H′,u′=vy=l√3πθ0sin(θ0/2),t=?
∴H′=[√3πθ0lsin(θ0/2)]t+12gt2
or t2+[2√3πθ0lsin(θ0/2)g]t−2H′g=0
∴t=−[2√3θ0lsin(θ0/2)g]±√[12π2θ20l2sin2(θ0/2)g2]+4×2H′lg2
=−[√3πθ0lsin(θ0/2)]±√3π2θ20l2sin2(θ0/2)+2H′gg
=−√3π(θ0/2)±√3π2θ20(θ20/4)+2H′gg
As θ0 is small so the terms with θ20 beign very very small can be neglected.
∴t=√2H′gg=√2H′g
Now, H′=H+l−l×l=H [∵cos(θ0/2)=1]
∴t=√2H′g=√2Hg
The horizontal distance travelled by bob after snapping
x=vxt=[√3lπθ0cos(θ0/2)]√2Hg=√3lπθ0×1×√2H/g=√6Hg×θ0lπj
At the time of snapping, the horizontal distance of the bob from point A is =lsin(θ0/2)=lθ0/2
Thus the distance of bob from A where it meets the ground is
=lθ02−√6Hglπθ0=lθ0[12−π√6Hg
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Advanced Problems For Competitions
20 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT EXERCISES WITH SOLUTIONS
19 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Short Answer Questions
104 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is θ0 the string snaps at 0=θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θ0 to be small, so that sinθ0≈θ0andcosθ0≈1.

View SolutionIn the figure, if the time taken by the bob to move from A to B is 0.5 second, the time period of the pendulum is____

View Solution
Knowledge Check
A ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
A√2h/gB√8h/gC√u2+2ghgDug+√2hgIf a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
A√LgB2√glsin(θ2)C√2glsinθD√2glA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibrium
A simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA simple pendulum bob of mass M and length l has one of its end fixed at the centre of a vertical circle as shown in figure. If θ=60∘ at the point P, the minimum speed u that should be given to the bob so that it completes vertical circle is :

View Solution
