A sine wave is travelling ina medium. The minium distance between the two particles, always having same speed is
λ4
λ3
λ2
λ
The correct Answer is:C
To solve the problem of finding the minimum distance between two particles in a sine wave that always have the same speed, we can follow these steps:
1. Understand the Wave Equation:
The displacement of a particle in a sine wave can be described by the equation:
y(x,t)=Asin(kx−ωt)
where A is the amplitude, k is the wave number, and ω is the angular frequency.
2. Determine Particle Velocity:
The velocity v of a particle in the wave can be derived from the displacement equation. The velocity is given by:
v=∂y∂t=ωAcos(kx−ωt)
However, we can also express the speed of the particle in terms of its position x:
v=ω√A2−x2
This indicates that the speed depends on the position x.
3. Identify Points with Same Speed:
To find two points where particles have the same speed, we can set the speeds of two particles at positions x1 and x2 equal to each other:
ω√A2−x21=ω√A2−x22
This simplifies to:
√A2−x21=√A2−x22
Squaring both sides gives:
A2−x21=A2−x22
Thus:
x21=x22
4. Find the Minimum Distance:
The solutions to x21=x22 are x1=x2 or x1=−x2. The minimum distance between two particles having the same speed occurs when one particle is at x=A and the other at x=−A. The distance between these two points is:
d=|A−(−A)|=|A+A|=2A
5. Consider the Wave's Wavelength:
The wavelength λ of the sine wave is related to the distance between repeating points in the wave. The minimum distance between two particles with the same speed occurs at half the wavelength:
Minimum distance=λ2
Conclusion:
The minimum distance between two particles that always have the same speed in a sine wave is:
λ2
The displacement of a particle in a sine wave can be described by the equation:
y(x,t)=Asin(kx−ωt)
where A is the amplitude, k is the wave number, and ω is the angular frequency.
The velocity v of a particle in the wave can be derived from the displacement equation. The velocity is given by:
v=∂y∂t=ωAcos(kx−ωt)
However, we can also express the speed of the particle in terms of its position x:
v=ω√A2−x2
This indicates that the speed depends on the position x.
To find two points where particles have the same speed, we can set the speeds of two particles at positions x1 and x2 equal to each other:
ω√A2−x21=ω√A2−x22
This simplifies to:
√A2−x21=√A2−x22
Squaring both sides gives:
A2−x21=A2−x22
Thus:
x21=x22
The solutions to x21=x22 are x1=x2 or x1=−x2. The minimum distance between two particles having the same speed occurs when one particle is at x=A and the other at x=−A. The distance between these two points is:
d=|A−(−A)|=|A+A|=2A
The wavelength λ of the sine wave is related to the distance between repeating points in the wave. The minimum distance between two particles with the same speed occurs at half the wavelength:
Minimum distance=λ2
The minimum distance between two particles that always have the same speed in a sine wave is:
λ2
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -2
9 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Worked out Examples
10 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer
9 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
Similar Questions
In sine wave , minimum distance between 2 particles always having same speed is
View SolutionA harmonic wave is travelling on a stretched string . At any particular instant , the smallest distance between two particles having same displacement , equal to half of amplitude is 8cm. Find the smallest separation between two particles which have same values of displacement (magnitude only) equal to half of amplitude.
View Solution
Knowledge Check
The particles of a medium oscillate about their equilibrium position, whenever a wave travels through that medium. The phase difference between the oscillations of two such practices varies
Awith time but not with distance separating themBwith distance separation them but not with timeCwith distance separating them as well as with timeDneither with distance separating them nor with time
A sine wave is travelling in a medium. A particular partile has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
View SolutionP,Q and R are three particle of a medium which lie on the x-axis. A sin wave of wavelength λ is travelling through the medium in the x-direction. P and Q always have the same speed. Whilem P and R always have the same velocity. The minimum distance between :-
View SolutionIn stationary waves, distance between a node and its nearest antinode is 20 cm . The phase difference between two particles having a separation of 60 cm will be
View SolutionFor a sine wave passing through a medium, let y be the displacement of a particle, v be its velocity and a be its acceleration :-
View SolutionDisplacement distance graph of two sound waves A and B, travelling in a medium, are shown in the diagram below.
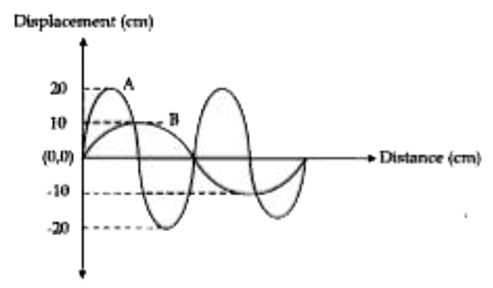
Study the two sound waves and compare their :
(i) Amplitudes, (ii) Wavelengths
View Solution(A) In a progressive wave, the phase diffe rence between two particles of a medium having a path difference λ is 2π
(R): The phase difference is directly propor tional to path difference between particles in progressive wave
View SolutionDisplacement distance graph of two sound waves A and B, travelling in a medium, are as shown in the diagram below:
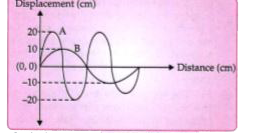
Study the two sound waves and compare their :
Amplitudes
View Solution
