A sinusoidal wave is genrated by moving the end of a string up and down, periodically. The genrated must apply the energy has ………..x and least power when the end of the string attached to genrated to genrated has ………..Y. the most suitable option which correctly fills blanks X and Y, is
maximum displacement, least acceleration
maximum displacement, maximum acceleration
least displacement, maximum acceleration
least displacement, least acceleration
The correct Answer is:c
To solve the question, we need to analyze the relationship between energy, power, displacement, and acceleration in the context of a sinusoidal wave generated on a string.
1. Understanding the Wave Equation:
The equation for a sinusoidal wave can be expressed as:
y(x,t)=Asin(kx−ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency.
2. Power in a Sinusoidal Wave:
The power P transmitted by the wave can be expressed in terms of the wave properties. The average power is given by:
P=12μω2A2cos2(kx−ωt)
where μ is the linear mass density of the string.
3. Condition for Least Power:
The power will be least when the cosine term is zero:
cos2(kx−ωt)=0
This occurs when kx−ωt=π2+nπ for integers n. Therefore, the least power corresponds to points where the wave is at its equilibrium position (displacement is zero).
4. Energy Considerations:
The energy in the wave is related to its displacement. The maximum energy is associated with maximum displacement (amplitude A). Conversely, when the displacement is least (zero), the energy is also at a minimum.
5. Acceleration:
The acceleration of a point on the string is given by:
a=−Aω2sin(kx−ωt)
The acceleration is maximum when the displacement is maximum (at the peaks of the wave).
6. Filling in the Blanks:
- For the first blank (X), the generator must apply energy at maximum displacement (which corresponds to maximum energy).
- For the second blank (Y), the least power occurs when the end of the string is at its equilibrium position (least displacement).
Thus, the correct options for the blanks are:
- X: Maximum energy
- Y: Least displacement
Final Answer:
The most suitable option which correctly fills the blanks X and Y is:
- X: Maximum energy
- Y: Least displacement
The equation for a sinusoidal wave can be expressed as:
y(x,t)=Asin(kx−ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency.
The power P transmitted by the wave can be expressed in terms of the wave properties. The average power is given by:
P=12μω2A2cos2(kx−ωt)
where μ is the linear mass density of the string.
The power will be least when the cosine term is zero:
cos2(kx−ωt)=0
This occurs when kx−ωt=π2+nπ for integers n. Therefore, the least power corresponds to points where the wave is at its equilibrium position (displacement is zero).
The energy in the wave is related to its displacement. The maximum energy is associated with maximum displacement (amplitude A). Conversely, when the displacement is least (zero), the energy is also at a minimum.
The acceleration of a point on the string is given by:
a=−Aω2sin(kx−ωt)
The acceleration is maximum when the displacement is maximum (at the peaks of the wave).
- For the first blank (X), the generator must apply energy at maximum displacement (which corresponds to maximum energy).
- For the second blank (Y), the least power occurs when the end of the string is at its equilibrium position (least displacement).
- X: Maximum energy
- Y: Least displacement
The most suitable option which correctly fills the blanks X and Y is:
- X: Maximum energy
- Y: Least displacement
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct
25 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A rope is attached at one end to a fixed vertical pole . It is stretched horizontal with a fixed value of tension T . Suppose at t=0, a pulse is generated by moving the free end of the rope up and down once with your hand. The pulse arrives at the pole at instant t.
Ignoring the effect of gravity, answer the following quetions.
In all the above, quetions we have considered a fixed value of tension. however, if tension in a given rope is increased and a pulse is genrated as described,
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves with an amplitude of 1.12 cm . The motion of the bar is continuous and is repeated regularly 120 times per second. The string has linear density of 117g/m. The other end of the string is attached to a mass 4.68 kg. The string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
The maximum magnitude of the transverse component of tension in the string is
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves with an amplitude of 1.12 cm . The motion of the bar is continuous and is repeated regularly 120 times per second. The string has linear density of 117g/m. The other end of the string is attached to a mass 4.68 kg. The string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
The maximum magnitude of the transverse speed is
View SolutionA transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
What is the transverse displacement y(in cm) when the minimum power transfer occurs
[Leave the answer in terms of π wherever it occurs]
View SolutionA transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
The maximum value of the transverse component of the tension (in newton)
View SolutionIn the figure shown a sinusoidal wave is generated at the end 'A'. The wave travels along positive x−axis and during its motions it encounter another string BC at the junction 'B' at x=0. The density of strings AB and BC and ρ and 9ρ respectively and their radii of cross sections are 2r and r. The wave funcation. amplitude and wavelength of incident wavs are respectively yr,Ar,λr and yt,At,λt repectively

Which of the following statement regarding phase difference, Δϕ between waves at x=0 is true ?
View SolutionIn the figure shown a sinusoidal wave is generated at the end 'A'. The wave travels along positive x−axis and during its motions it encounter another string BC at the junction 'B' at x=0. The density of strings AB and BC and ρ and 9ρ respectively and their radii of cross sections are 2r and r. The wave funcation. amplitude and wavelength of incident wavs are respectively yr,Ar,λr and yt,At,λt repectively

The ratio of amplitudes Ar to At is (i.e. A_(r) : A_(t)) will be
View SolutionIn the figure shown a sinusoidal wave is generated at the end 'A'. The wave travels along positive x−axis and during its motions it encounter another string BC at the junction 'B' at x=0. The density of strings AB and BC and ρ and 9ρ respectively and their radii of cross sections are 2r and r. The wave funcation. amplitude and wavelength of incident wavs are respectively yr,Ar,λr and yt,At,λt repectively

The ratio of wavelengths λr to λt (i.e. λr:λt) will be
View SolutionIn the figure shown a sinusoidal wave is generated at the end A the wave travels along positive x-axis and during its motion it encounter another string BD at the junction 'B'atx=0.The density of string AB and BC are ρand9ρrespectively and their radii of cross sections are 2randr. The wave function amplitude and wavelength of incident wave are respectively ypAiandλr Similarly for reflected and transmitted wave these peremeters are yr,Ar,λrandyi,Ai,λi
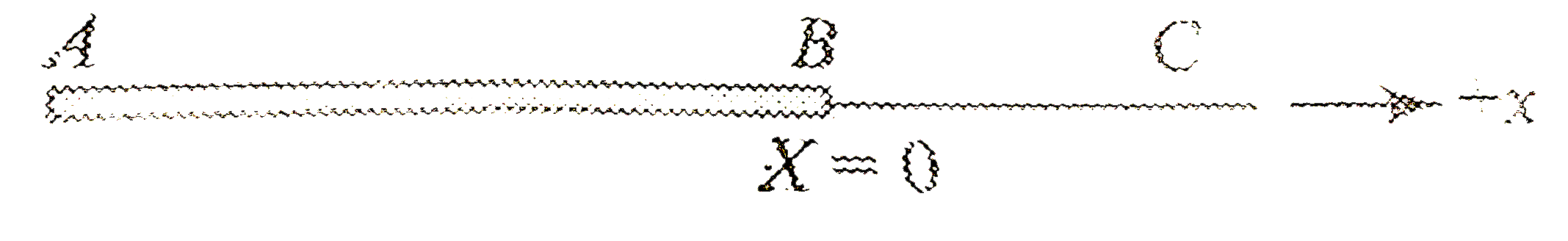
Which of the following statement regarding phase difference Δϕ between waves at x=0 is true?
View Solution
