A transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves with an amplitude of 1.12 cm . The motion of the bar is continuous and is repeated regularly 120 times per second. The string has linear density of 117g/m. The other end of the string is attached to a mass 4.68 kg. The string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
The maximum magnitude of the transverse speed is
10.884 m/s
8.44 m/s
844 m/s
none of these
The correct Answer is:B
To find the maximum magnitude of the transverse speed of the wave generated on the string, we can follow these steps:
Step 1: Identify the given parameters
- Amplitude of the wave, A=1.12cm=1.12×10−2m
- Frequency of the wave, f=120Hz
- Linear density of the string, μ=117g/m=0.117kg/m
- Mass hanging from the string, m=4.68kg
Step 2: Calculate the angular frequency ω
The angular frequency ω is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×120=240πrad/s
Step 3: Determine the wave speed v
The wave speed v on the string can be calculated using the formula:
v=√Tμ
Where T is the tension in the string, which can be calculated as:
T=mg=4.68×9.81N≈45.92N
Now substituting T and μ:
v=√45.920.117≈√392.24≈19.8m/s
Step 4: Calculate the maximum transverse speed
The maximum transverse speed vtransverse max can be calculated using the formula:
vtransverse max=ωA
Substituting the values of ω and A:
vtransverse max=(240π)×(1.12×10−2)
Calculating this:
vtransverse max=240×3.14×1.12×10−2≈8.44m/s
Conclusion
The maximum magnitude of the transverse speed is approximately 8.44m/s.
---
- Amplitude of the wave, A=1.12cm=1.12×10−2m
- Frequency of the wave, f=120Hz
- Linear density of the string, μ=117g/m=0.117kg/m
- Mass hanging from the string, m=4.68kg
The angular frequency ω is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×120=240πrad/s
The wave speed v on the string can be calculated using the formula:
v=√Tμ
Where T is the tension in the string, which can be calculated as:
T=mg=4.68×9.81N≈45.92N
Now substituting T and μ:
v=√45.920.117≈√392.24≈19.8m/s
The maximum transverse speed vtransverse max can be calculated using the formula:
vtransverse max=ωA
Substituting the values of ω and A:
vtransverse max=(240π)×(1.12×10−2)
Calculating this:
vtransverse max=240×3.14×1.12×10−2≈8.44m/s
The maximum magnitude of the transverse speed is approximately 8.44m/s.
Similar Questions
A transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves with an amplitude of 1.12 cm . The motion of the bar is continuous and is repeated regularly 120 times per second. The string has linear density of 117g/m. The other end of the string is attached to a mass 4.68 kg. The string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
The maximum magnitude of the transverse component of tension in the string is
View SolutionA transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
The maximum value of the transverse component of the tension (in newton)
View Solution
Knowledge Check
A string of mass 3 kg is under tension of 400 N. the length of the stretched string is 25 cm. if the transverse jerk is stuck at one end of the string how long does the disturbance take to reach the other end?
A0.043sB4.33SC0.055 sD0.034 s
A transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
What is the transverse displacement y(in cm) when the minimum power transfer occurs
[Leave the answer in terms of π wherever it occurs]
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
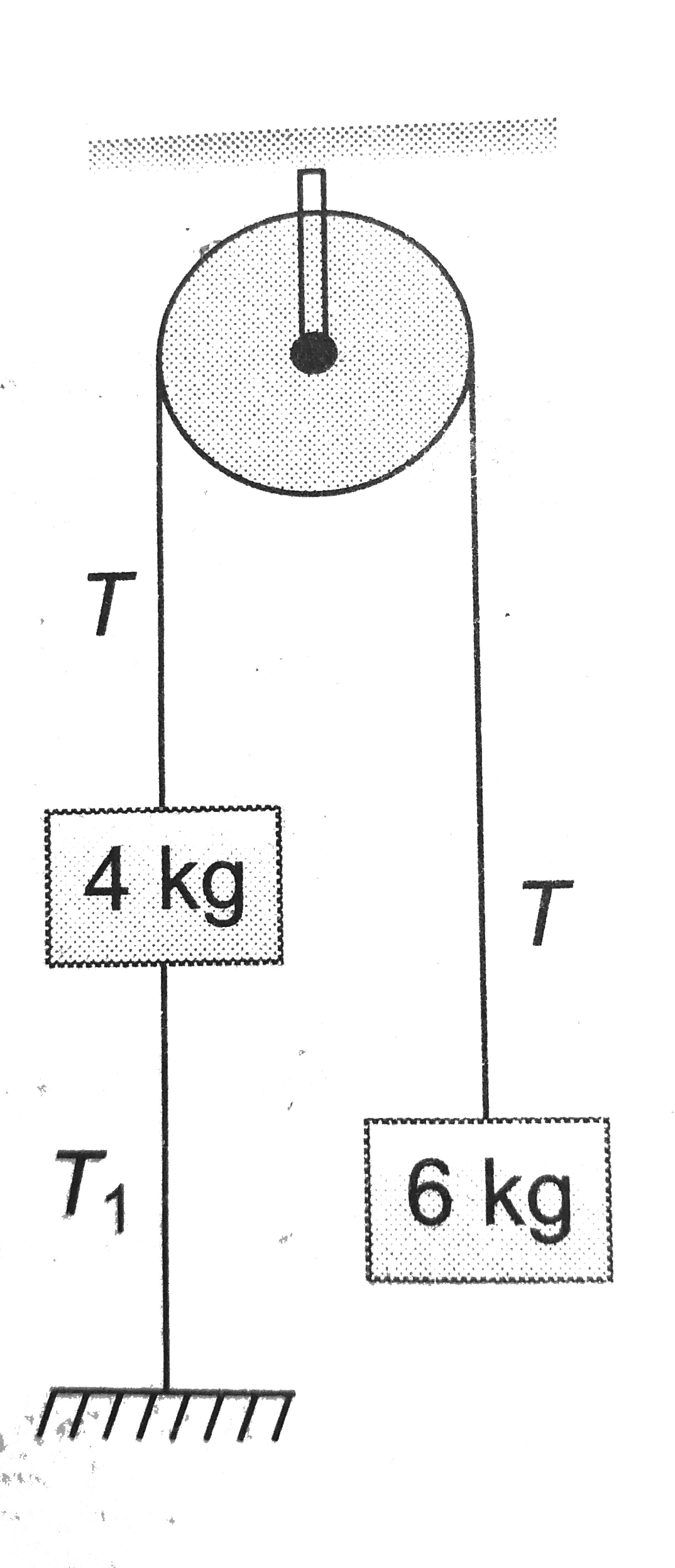
View SolutionA block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20J in 1s.
View Solution
