A small 0.500 kg object moves on a frictionless horizontal table in a circular path of radius 1.00 m. The angular speed is 6.28rad/s. The object is attached to a string of negligible mass that passes through a small hole in the table at the center of the circle. Someone under the table begins to pull the string downward to make the circle smaller. If the string will toler ate a tension of no more than 105 N, what is the radius of the smallest possible circle on which the object can move?
0.376 m
0.434 m
0.573 m
0.188 m
The correct Answer is:C
To solve the problem, we need to determine the radius of the smallest possible circle on which the object can move while ensuring that the tension in the string does not exceed 105 N. We will use the concepts of circular motion and centripetal force.
1. Identify the given values:
- Mass of the object, m=0.500kg
- Angular speed, ω=6.28rad/s
- Maximum tension in the string, Tmax=105N
2. Understand the relationship between tension and centripetal force:
The tension in the string provides the necessary centripetal force to keep the object moving in a circular path. The centripetal force Fc required for circular motion is given by:
Fc=m⋅ac
where ac is the centripetal acceleration. The centripetal acceleration can also be expressed in terms of angular speed and radius r:
ac=ω2⋅r
Therefore, we can write:
Fc=m⋅(ω2⋅r)
3. Set the centripetal force equal to the tension:
Since the tension is providing the centripetal force, we have:
T=m⋅(ω2⋅r)
Setting T equal to the maximum tension:
105=0.500⋅(6.282⋅r)
4. Calculate ω2:
First, calculate ω2:
ω2=(6.28)2=39.4784rad2/s2
5. Substitute ω2 into the tension equation:
Substitute ω2 into the equation:
105=0.500⋅(39.4784⋅r)
6. Solve for r:
Rearranging the equation to solve for r:
r=1050.500⋅39.4784
r=10519.7392≈5.31m
Final Answer:
The radius of the smallest possible circle on which the object can move is approximately 5.31 m.
- Mass of the object, m=0.500kg
- Angular speed, ω=6.28rad/s
- Maximum tension in the string, Tmax=105N
The tension in the string provides the necessary centripetal force to keep the object moving in a circular path. The centripetal force Fc required for circular motion is given by:
Fc=m⋅ac
where ac is the centripetal acceleration. The centripetal acceleration can also be expressed in terms of angular speed and radius r:
ac=ω2⋅r
Therefore, we can write:
Fc=m⋅(ω2⋅r)
Since the tension is providing the centripetal force, we have:
T=m⋅(ω2⋅r)
Setting T equal to the maximum tension:
105=0.500⋅(6.282⋅r)
First, calculate ω2:
ω2=(6.28)2=39.4784rad2/s2
Substitute ω2 into the equation:
105=0.500⋅(39.4784⋅r)
Rearranging the equation to solve for r:
r=1050.500⋅39.4784
r=10519.7392≈5.31m
The radius of the smallest possible circle on which the object can move is approximately 5.31 m.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS(Linked Comprehension)3videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PROBLEMS41videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
A puck of mas m=1.50 kg slides in a circle of radius r=25.0 cm on a frictionless table while attached to a hanging cylinder of mass M=2.50 kg by means of a cord that extends through a hole in the table. What speed keeps the cylinder at rest?
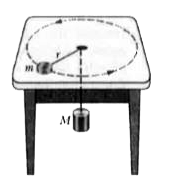 View Solution
View SolutionTwo identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
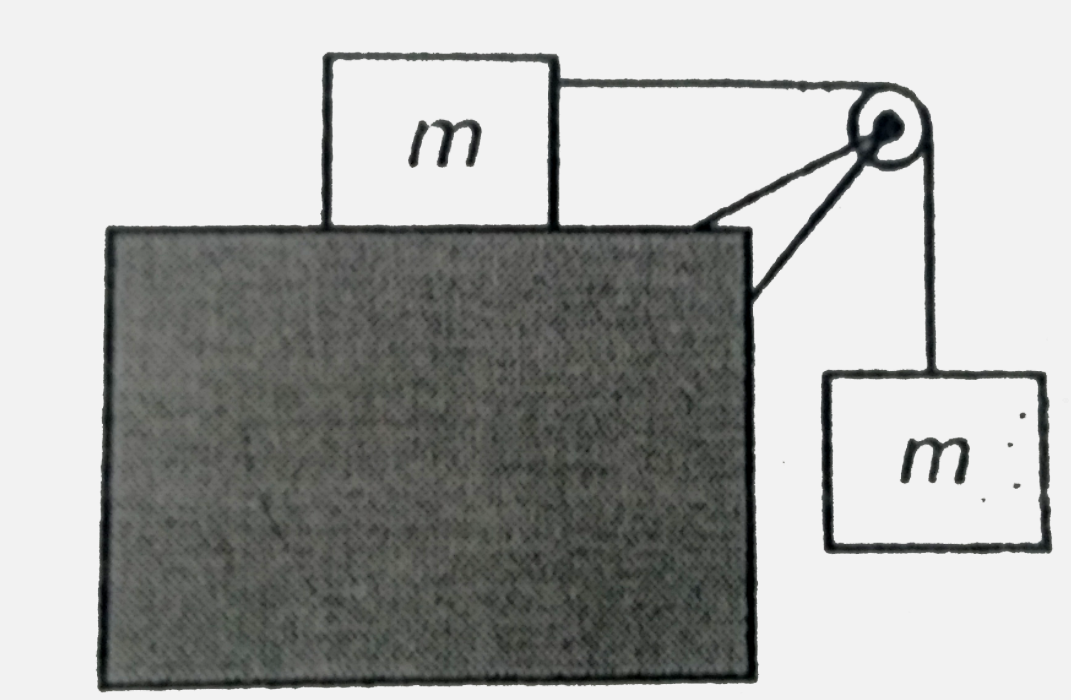 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Speed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
A10 m/sB5 m/sC20 m/sD30 m/s - Question 2 - Select One
A small body attached at the end of an inextensible string completes a vertical circle , then its
Aangular velocity remains constantBangular momentum reamains constantCtotal mechanical energy remains constantDlinear momentum reamains constant - Question 3 - Select One
A stone of mass 1/2 kg is whriled round the end of a piece of string in a horizontal circle of radius half a meter with a uniform speed of 1m/s. The tension in the string is
A25×103 dynesB105 dynesC5×104 dynesD4×105 dynes
In Fig. 6-43, a 15 kg sled is attached to a 2.0 kg sand box by a string of negligible mass, wrapped over a pulley of negligible mass and friction. The coefficient of kinetic friction between the sled and table top is 0.040. Find (a) the acceleration of the sled and (b) the tension of the string.
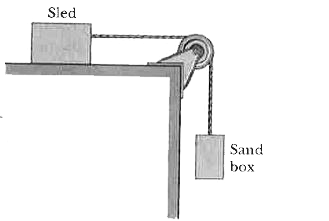 View Solution
View SolutionIn 5.00 s, a 2.00 kg stone moves in a horizontal circle of radius 2.00 m from rest to an angular speed of 4.00 rev/s. What are the stone's (a) average angular acceleration and (b) rotational inertia around the circle's center?
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA small mass attached to a string rotates on a frictionless table top as shown in Fig. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
 View Solution
View SolutionA particle of mass 2 kg is on a smooth horizontal table and moves in a circular path of radius 0.6 m. The height of the table from the ground is 0.8 m. If the angular speed of the particle is 12 rad s−1 , the magnitude of its angular momentum about a point on the ground right under the centre of the circle is
View Solution

