A small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
a. At what angle from the vertical of the ball's trajectory, will the tension in the thread disappear?
b. What will be the highest point from the lowermost point of circular track, to which it will rise?
The correct Answer is:a. cos−1(2/3); b. 50l54
To solve the problem step by step, we will break it down into two parts as specified in the question.
Part (a): Finding the angle from the vertical at which the tension in the thread disappears.
1. Understanding the Setup:
- A ball is suspended from point O by a thread of length l.
- A nail is driven into the wall at point A, which is at a distance l2 below O.
- The ball is drawn to a horizontal position and released.
2. Analyzing Forces at Point P:
- When the ball swings down, it will follow a circular path until it reaches point P, where the tension in the thread becomes zero.
- At point P, the only forces acting on the ball are its weight mg acting downwards and the component of this weight that provides the centripetal force.
3. Setting Up the Equation:
- At point P, the centripetal force required for circular motion is provided by the component of the gravitational force acting along the direction of the radius.
- The equation can be written as:
mgcos(θ)=mv2Pr
- Here, r=l2 (the radius of the circular path), and vP is the velocity at point P.
4. Using Conservation of Energy:
- The potential energy lost when the ball moves from the horizontal position to point P is converted into kinetic energy.
- The change in potential energy is:
ΔPE=mg(l2(1−cos(θ)))
- The kinetic energy at point P is:
KE=12mv2P
- Setting these equal gives:
mg(l2(1−cos(θ)))=12mv2P
5. Substituting v2P:
- From the centripetal force equation, we have:
v2P=glcos(θ)2
- Substituting this into the energy equation:
mg(l2(1−cos(θ)))=12m(glcos(θ)2)
- Simplifying gives:
g(l2(1−cos(θ)))=glcos(θ)4
6. Solving for cos(θ):
- Canceling g and l (assuming they are non-zero):
2(1−cos(θ))=cos(θ)
- Rearranging gives:
2−2cos(θ)=cos(θ)⟹2=3cos(θ)⟹cos(θ)=23
7. Final Result for Part (a):
- Therefore, the angle θ is:
θ=cos−1(23)
Part (b): Finding the highest point from the lowermost point of the circular track.
1. Finding the Velocity at Point P:
- We already found that:
v2P=glcos(θ)2
- Substituting cos(θ)=23:
v2P=gl⋅232=gl3
- Thus, vP=√gl3.
2. Projectile Motion After Point P:
- After reaching point P, the ball will move in projectile motion.
- The maximum height h reached in projectile motion can be calculated using:
h=v2Psin2(θ)2g
3. Finding sin(θ):
- Using sin2(θ)+cos2(θ)=1:
sin2(θ)=1−(23)2=1−49=59
4. Calculating Maximum Height:
- Substituting vP and sin2(θ):
h=(gl3)⋅592g=5l54
5. Total Height from the Lowermost Point:
- The total height from the lowest point of the circular track is the height gained plus the distance from point A to the lowest point:
H=l2+5l54=27l54+5l54=32l54=16l27
Final Results:
- Part (a): θ=cos−1(23)
- Part (b): The highest point from the lowermost point of the circular track is 16l27.
- A ball is suspended from point O by a thread of length l.
- A nail is driven into the wall at point A, which is at a distance l2 below O.
- The ball is drawn to a horizontal position and released.
- When the ball swings down, it will follow a circular path until it reaches point P, where the tension in the thread becomes zero.
- At point P, the only forces acting on the ball are its weight mg acting downwards and the component of this weight that provides the centripetal force.
- At point P, the centripetal force required for circular motion is provided by the component of the gravitational force acting along the direction of the radius.
- The equation can be written as:
mgcos(θ)=mv2Pr
- Here, r=l2 (the radius of the circular path), and vP is the velocity at point P.
- The potential energy lost when the ball moves from the horizontal position to point P is converted into kinetic energy.
- The change in potential energy is:
ΔPE=mg(l2(1−cos(θ)))
- The kinetic energy at point P is:
KE=12mv2P
- Setting these equal gives:
mg(l2(1−cos(θ)))=12mv2P
- From the centripetal force equation, we have:
v2P=glcos(θ)2
- Substituting this into the energy equation:
mg(l2(1−cos(θ)))=12m(glcos(θ)2)
- Simplifying gives:
g(l2(1−cos(θ)))=glcos(θ)4
- Canceling g and l (assuming they are non-zero):
2(1−cos(θ))=cos(θ)
- Rearranging gives:
2−2cos(θ)=cos(θ)⟹2=3cos(θ)⟹cos(θ)=23
- Therefore, the angle θ is:
θ=cos−1(23)
- We already found that:
v2P=glcos(θ)2
- Substituting cos(θ)=23:
v2P=gl⋅232=gl3
- Thus, vP=√gl3.
- After reaching point P, the ball will move in projectile motion.
- The maximum height h reached in projectile motion can be calculated using:
h=v2Psin2(θ)2g
- Using sin2(θ)+cos2(θ)=1:
sin2(θ)=1−(23)2=1−49=59
- Substituting vP and sin2(θ):
h=(gl3)⋅592g=5l54
- The total height from the lowest point of the circular track is the height gained plus the distance from point A to the lowest point:
H=l2+5l54=27l54+5l54=32l54=16l27
- Part (a): θ=cos−1(23)
- Part (b): The highest point from the lowermost point of the circular track is 16l27.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge −q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30∘ with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
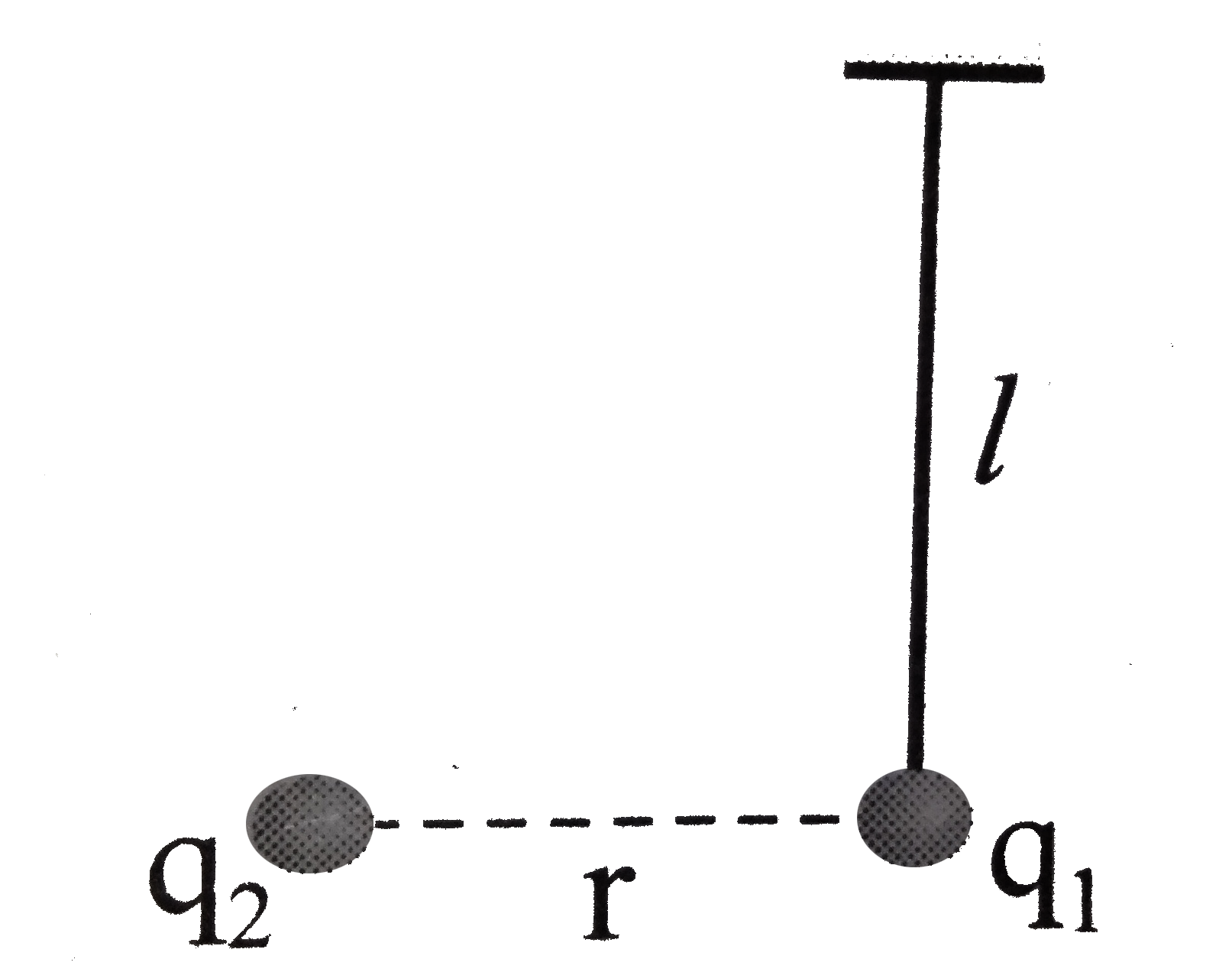
View SolutionA ball is thrown from a point in level with velocity u and at a horizontal distance r from the top os a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ?
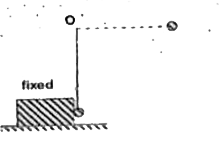
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
View SolutionA sphere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
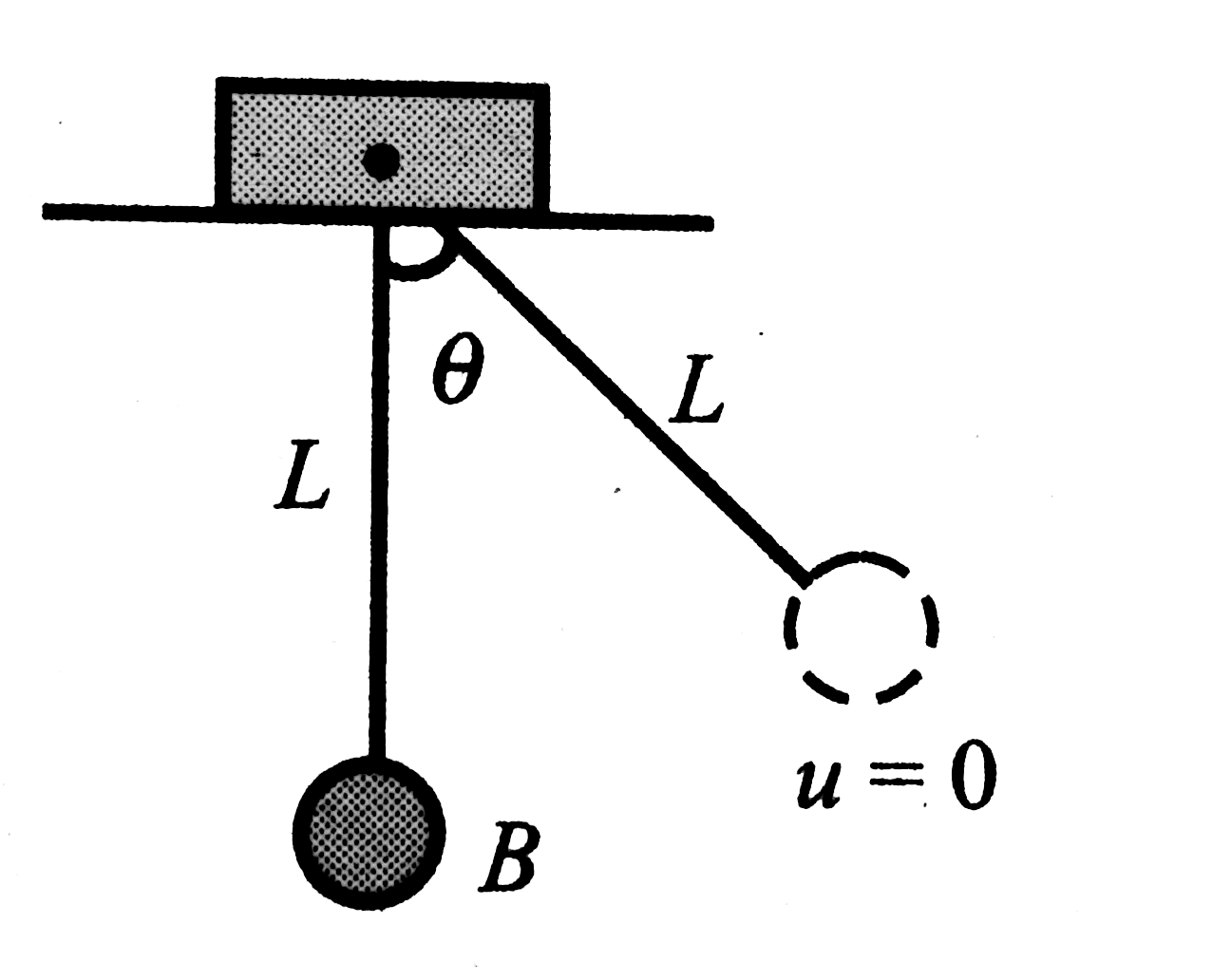
Tension in string when it is vertical, is
View SolutionA particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is (a)the thread is displacement througha small angle away from the vertical and (b) the ball is released. Find the period of obcillation of pendulum. Consider both cases
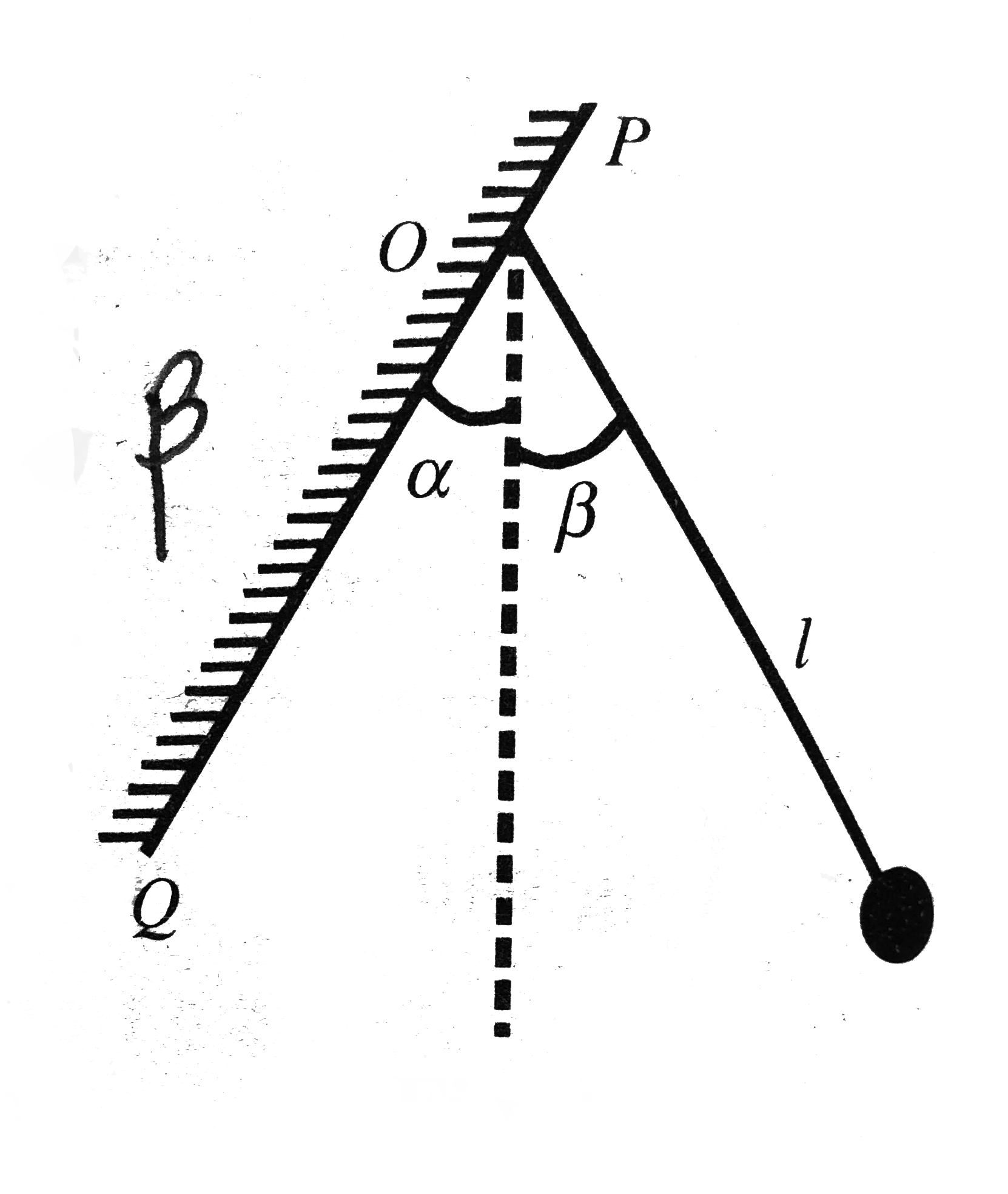
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.
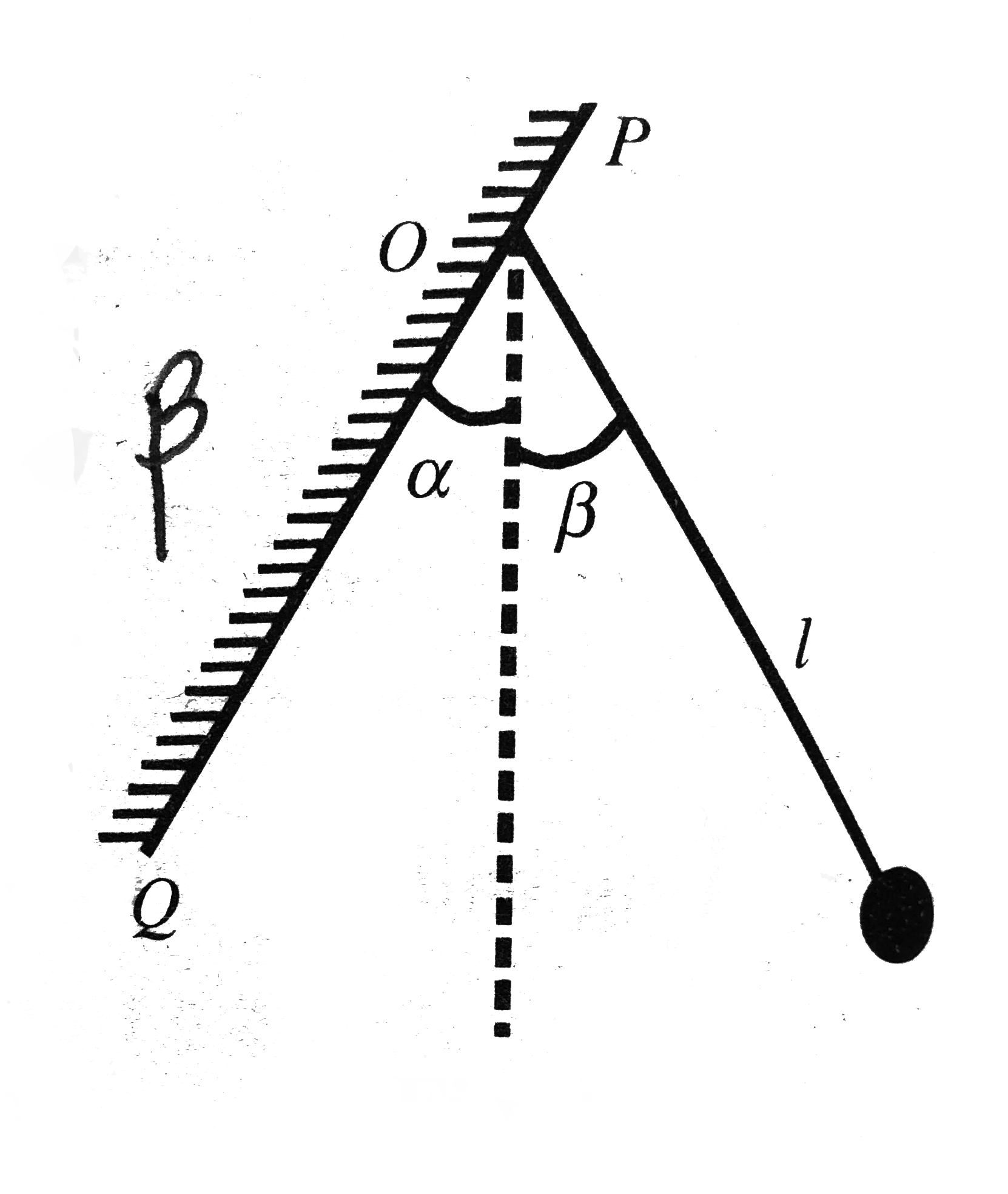
Consider both cases
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.
View Solution
