Question

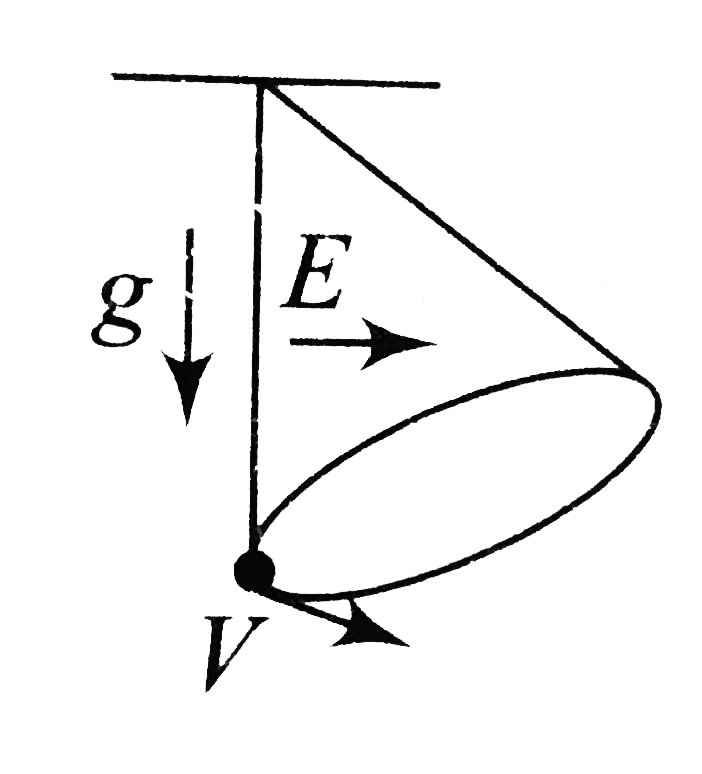
A particle of mass $m=0.1kg$ and having positive charge $q=75\mu C$ is suspended from a point by a thread of length $l=10cm$. In the space, a uniform horizontal electric field $E={10}^{4}N{C}^{-1}$ exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed $v(g=10m{s}^{-2})$.

Explanation

To solve the problem, we need to find the radius of the circular path and the speed of the charged particle moving in a uniform electric field. Here's a step-by-step solution:

Step 1: Understanding the Forces Acting on the Particle
The particle of mass \( m = 0.1 \, \text{kg} \) and charge \( q = 75 \, \mu C = 75 \times 10^{-6} \, C \) is suspended by a thread of length \( l = 10 \, \text{cm} = 0.1 \, \text{m} \). The uniform electric field \( E = 10^4 \, \text{N/C} \) acts horizontally.

When the particle is displaced and then projected horizontally, it will move in a circular path at an angle \( \theta \) with respect to the vertical.

Step 2: Determine the Angle of Equilibrium
In equilibrium, the forces acting on the particle are balanced. The vertical component of the tension \( T \) balances the weight \( mg \), and the horizontal component of the tension balances the electric force \( F_e = qE \).

1. Vertical Forces:
\( T \cos \theta = mg \)

2. Horizontal Forces:
\( T \sin \theta = qE \)

Dividing these two equations gives:
\( \tan \theta = \frac{qE}{mg} \)

Step 3: Substitute Values to Find \( \theta \)
Substituting the known values:
- \( q = 75 \times 10^{-6} \, C \)
- \( E = 10^4 \, N/C \)
- \( m = 0.1 \, kg \)
- \( g = 10 \, m/s^2 \)

Calculating:
\( \tan \theta = \frac{(75 \times 10^{-6})(10^4)}{(0.1)(10)} = \frac{0.75}{1} = 0.75 \)
Thus,
\( \theta = \tan^{-1}(0.75) \approx 36.87^\circ \text{ (or } 37^\circ\text{)} \)

Step 4: Calculate the Radius of the Circular Path
The radius \( r \) of the circular path can be found using:
\( r = l \sin \theta \)
Substituting \( l = 0.1 \, m \) and \( \sin 37^\circ = \frac{3}{5} \):
\( r = 0.1 \times \frac{3}{5} = 0.06 \, m \)

Step 5: Calculate the Speed of the Particle
The net force acting towards the center of the circular path provides the centripetal force:
\( T \sin \theta + qE \cos \theta - mg \sin \theta = \frac{mv^2}{r} \)

From the vertical force equation, we can find \( T \):
\( T = \frac{mg}{\cos \theta} \)

Substituting \( \theta = 37^\circ \):
\( T = \frac{(0.1)(10)}{\cos 37^\circ} = \frac{1}{\frac{4}{5}} = 1.25 \, N \)

Now substituting \( T \) into the centripetal force equation:
\( 1.25 \sin 37^\circ + (75 \times 10^{-6})(10^4) \cos 37^\circ - (0.1)(10) \sin 37^\circ = \frac{0.1 v^2}{0.06} \)

Calculating each term:
- \( \sin 37^\circ = \frac{3}{5} \)
- \( \cos 37^\circ = \frac{4}{5} \)

Substituting:
\( 1.25 \cdot \frac{3}{5} + (75 \times 10^{-6})(10^4) \cdot \frac{4}{5} - (0.1)(10) \cdot \frac{3}{5} = \frac{0.1 v^2}{0.06} \)

Calculating:
\( 0.75 + 0.6 - 0.6 = \frac{0.1 v^2}{0.06} \)
\( 0.75 = \frac{0.1 v^2}{0.06} \)
\( 0.75 \cdot 0.06 = 0.1 v^2 \)
\( 0.045 = 0.1 v^2 \)
\( v^2 = 0.45 \quad \Rightarrow \quad v = \sqrt{0.45} \approx 0.67 \, m/s \)

Final Answers
- Radius of the circle: \( r = 0.06 \, m \)
- Speed of the particle: \( v \approx 0.67 \, m/s \)