A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is (a)the thread is displacement througha small angle away from the vertical and (b) the ball is released. Find the period of obcillation of pendulum. Consider both cases 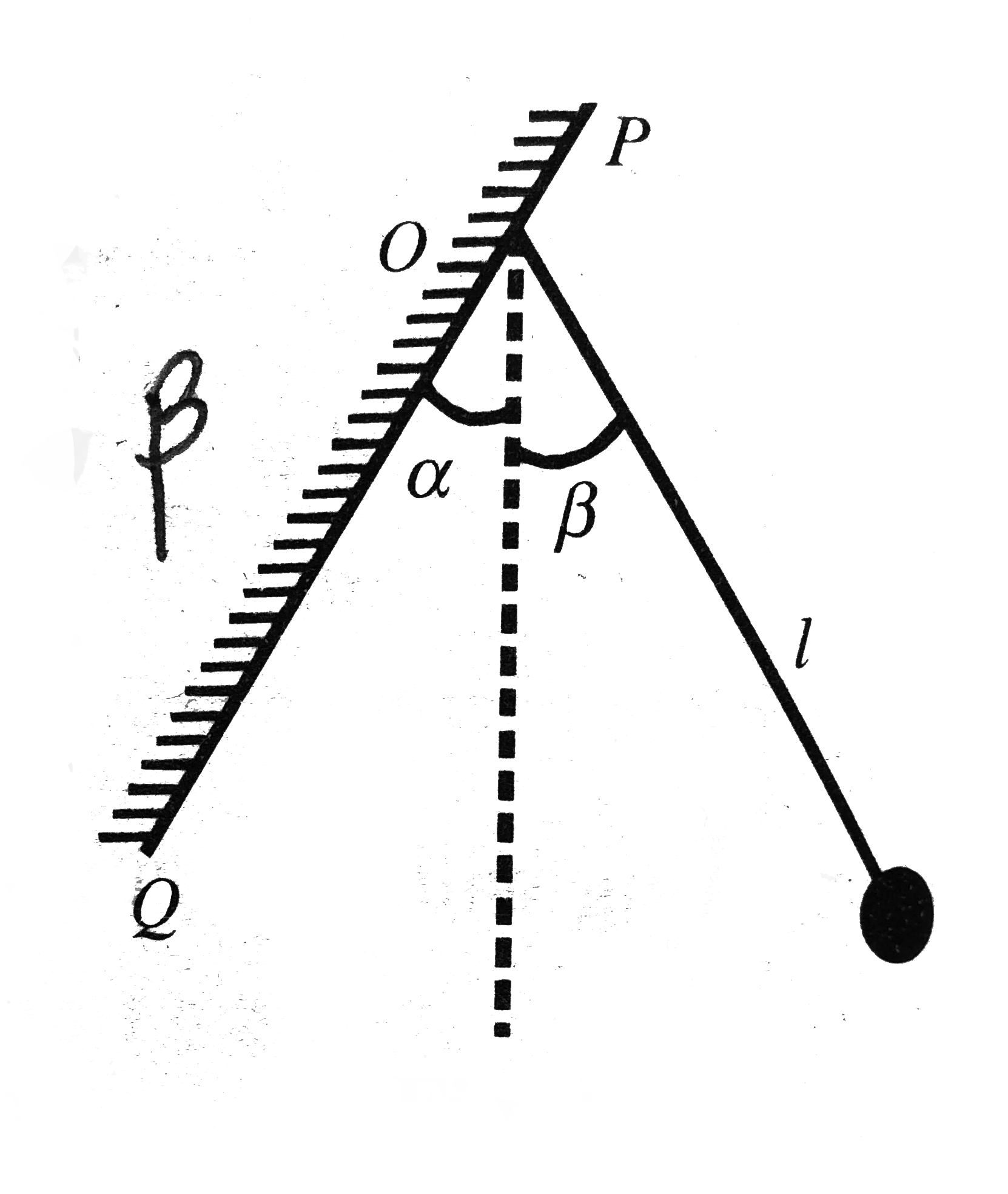
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.
If α>β, the ball does not collide which the wall and it performed full oscillation like simple pendulum. Thus,
Period=2π√lg
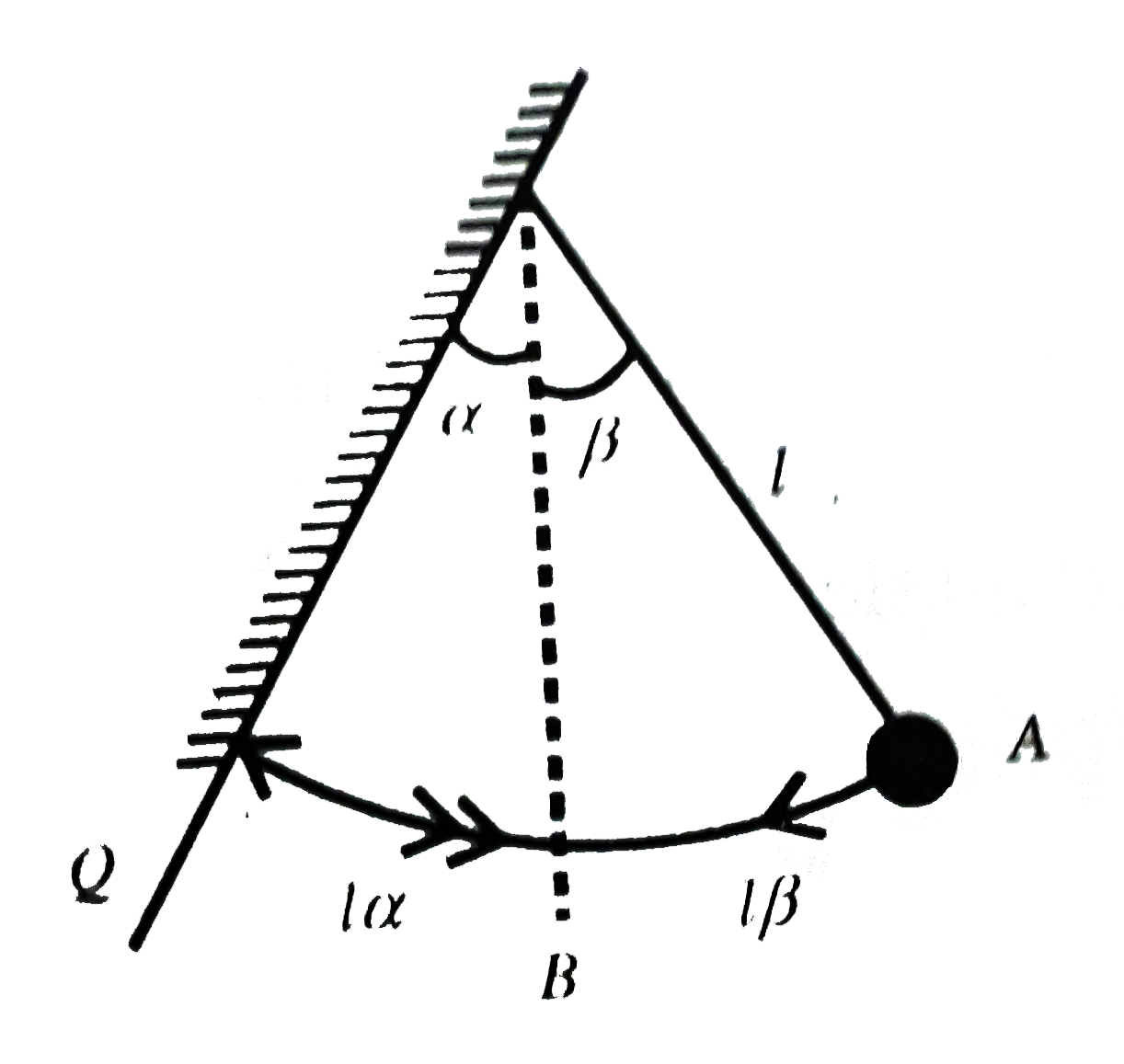
b. If α<β, the ball collide with the wall and rebounds with same speed the motion of ball from AandQ is one part of a simple pendulum time Period of ball=2(tAQ
Consider A as the starting point (t=0), equition of motion is x(t)=Acosωt.
x(t)=lβcosωt, because amplitude =A=lβ
Time from A to Q is the time t when x becomes - l alpha<br>implies - l alpha - l beta cos omega t implies t = t_(AQ)=l/ωcos−1(−αβ)
The return path from QandA will involve the same time interval. Hence time period of ball =2tAQ
=2ωcos−1(−αβ)=2√tgcos−1(−αβ)
=2π√lg−2√lgcos−1(αβ)
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.
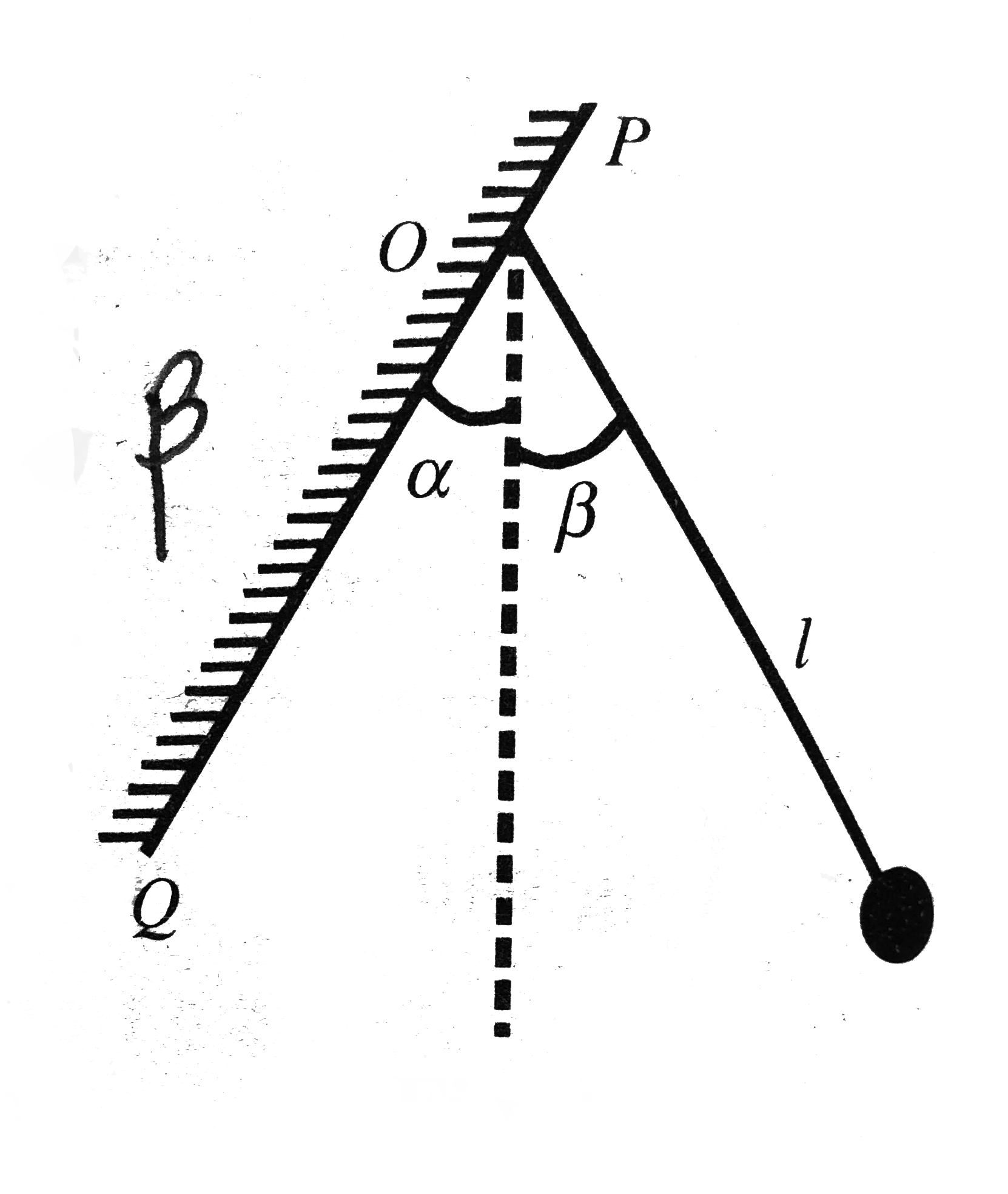
Consider both cases
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.
View SolutionA sphere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
View SolutionA ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
View SolutionA ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
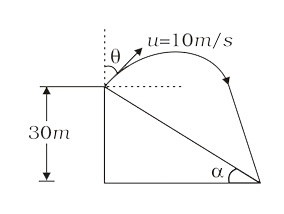
The time of flight of the ball is:
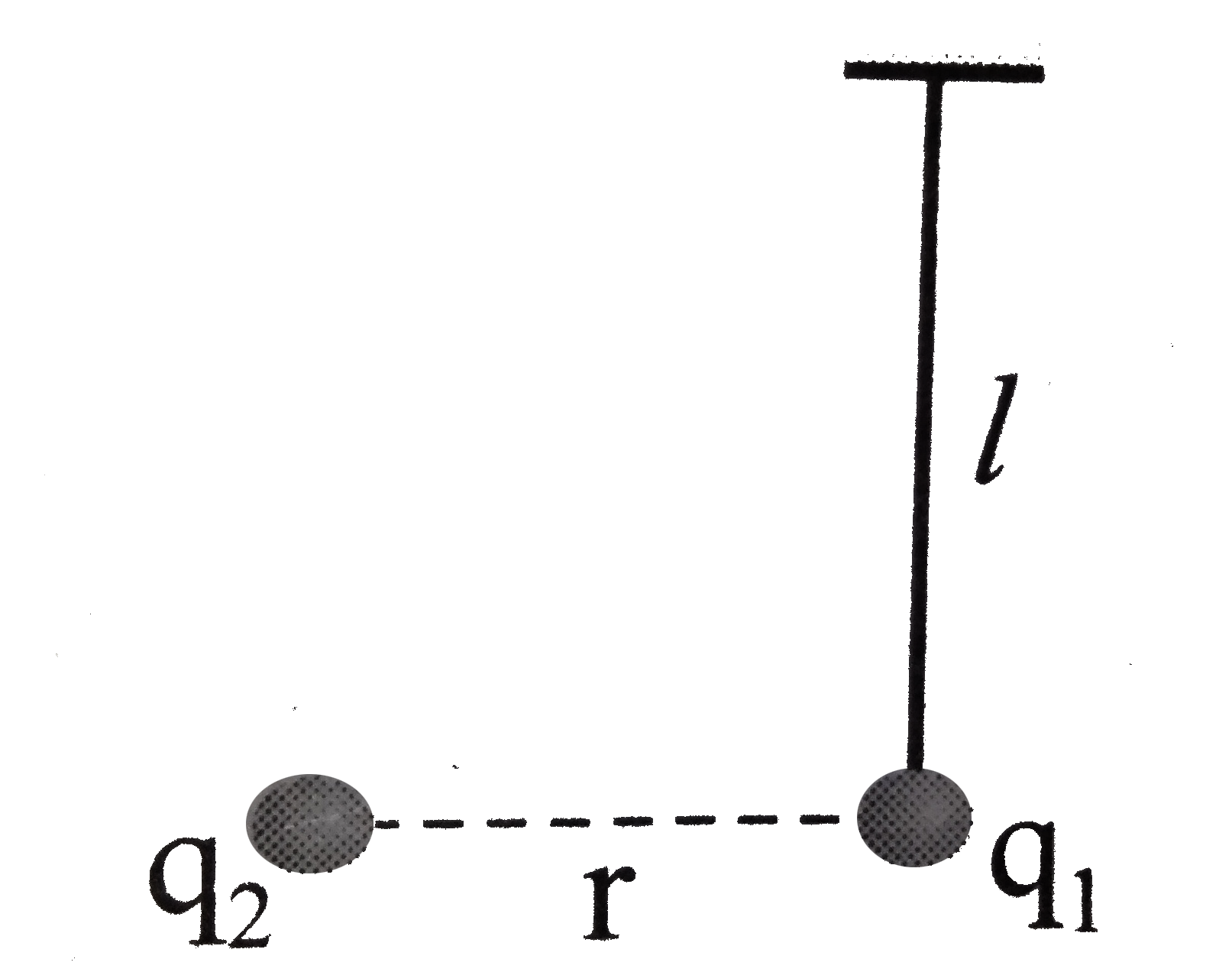
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
View SolutionA small ball is suspended from point O by a thread of length l. A nail is driven into the wall at a distance of l/2 below O, at A. The ball is drawn aside so that the thread takes up a horizontal position at the level of point O and then released. Find
a. At what angle from the vertical of the ball's trajectory, will the tension in the thread disappear?
b. What will be the highest point from the lowermost point of circular track, to which it will rise?
View SolutionA ball strikes the ground at an angle α. and rebound at an angle β. with the verticlal as shown in the figure .Then ,

View SolutionA conical pendulum of length L makes an angle θ with the vertical. The time period will be

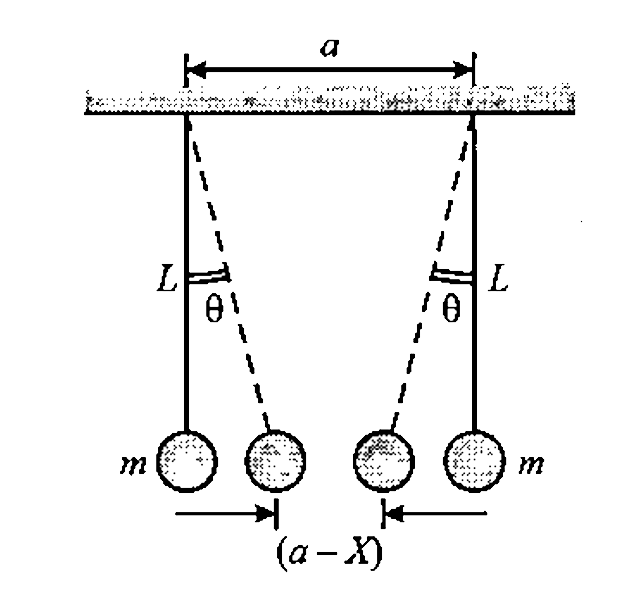
View SolutionTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
View SolutionConsider a container having an inclined wall, inclined an angle θ with horizontal as shown in Fig. Calculate the force per unit width on the wall.

View Solution
