A small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
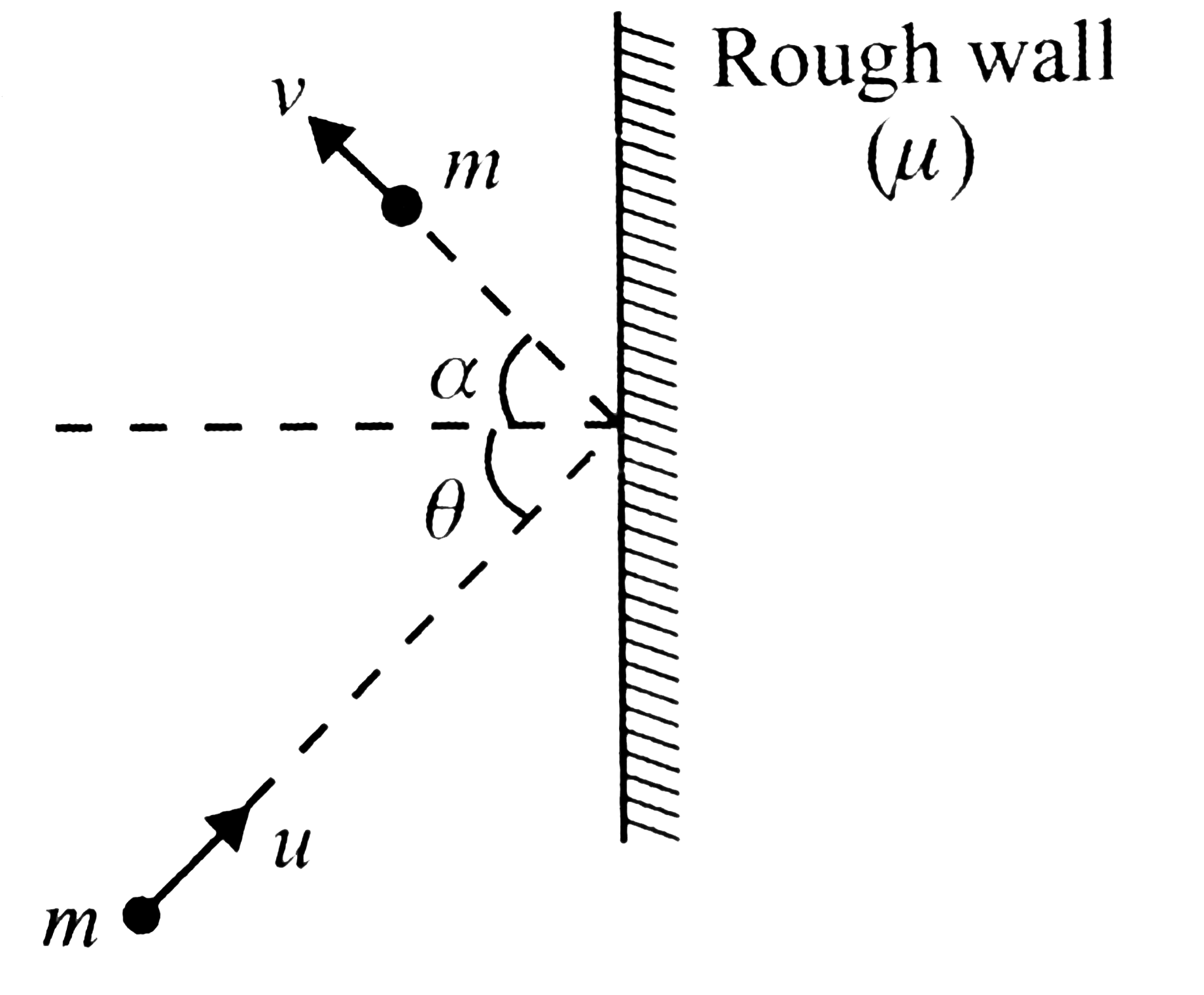
A small ball of mass m collides with as rough wal having coeficient of friction mu at an angle theta with the normal to the wall. If after collision the ball moves wilth angle alpha with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

mvcosα−[m(−ucosθ)]=∫Ndt
mvsinα−μsinθ=−μ∫Ndt
ande=vcosαucosθ⇒vcosα=eucosθ……….i
ormvsinα−μsinθ−μ(mvcosα+μcosθ)……….ii
Fromeqniandiiv=usinα[sinθ−μcosθ(e+1)]

Updated on:21/07/2023
|
Class 11PHYSICSCENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?

    A1−e1+e
    Be−1e+1
    C1+e1−e
    De+1e−1

  • A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?

    A1−e1+e
    B1+e1−e
    Ce−1e+1
    De+1e−1