A small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
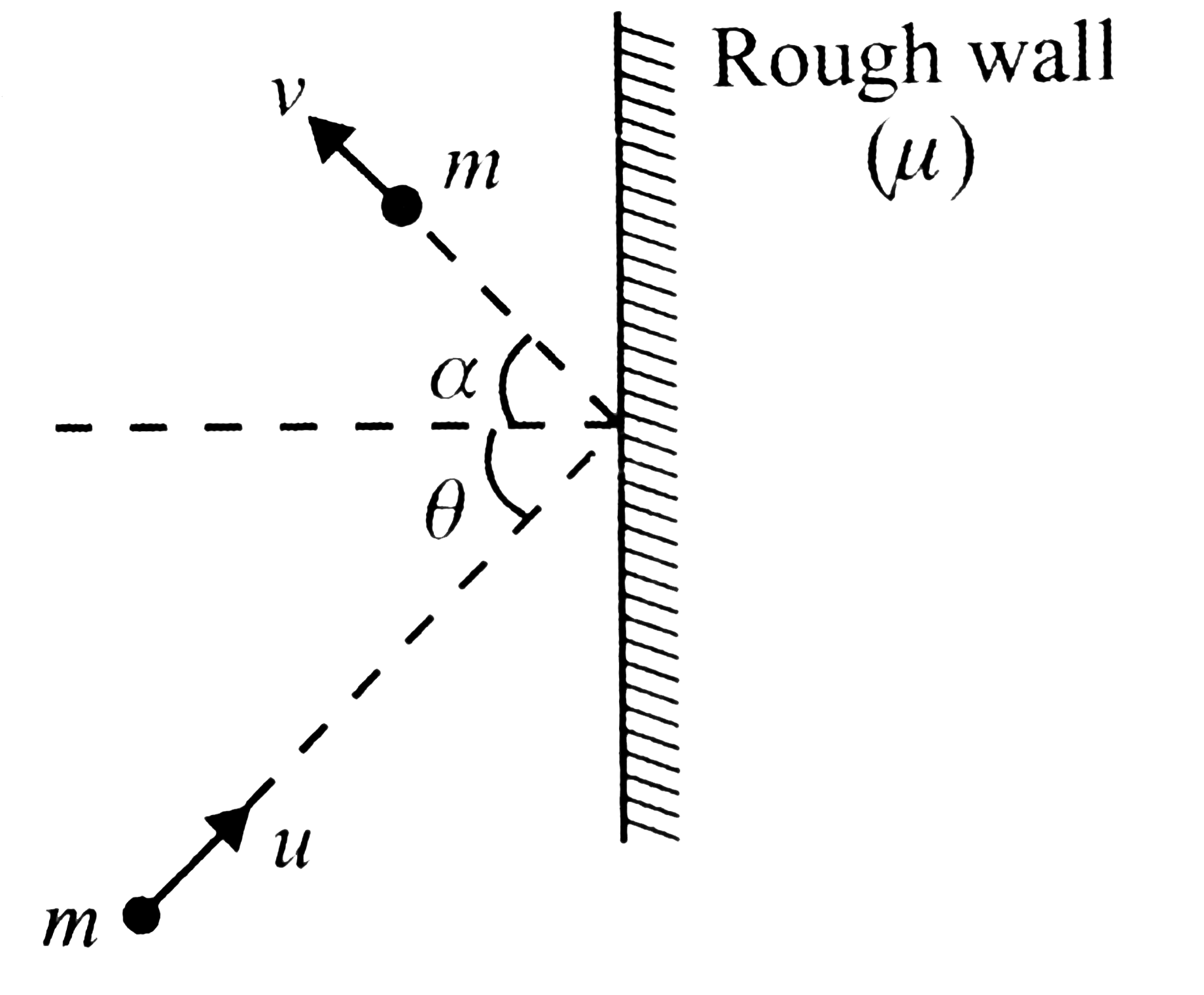
mvcosα−[m(−ucosθ)]=∫Ndt
mvsinα−μsinθ=−μ∫Ndt
ande=vcosαucosθ⇒vcosα=eucosθ……….i
ormvsinα−μsinθ−μ(mvcosα+μcosθ)……….ii
Fromeqniandiiv=usinα[sinθ−μcosθ(e+1)]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
 View Solution
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
Knowledge Check
- Question 1 - Select One or More
A ball moving with velocity u strikes a smooth horizontal floor at an angle α with the normal to the surface at the point of contact . After collision , ball moves with velocity v at an angle β with the normal . Assume e as the coefficient of restitution .
Atanα=etanβBImpulse applied by the surface on the ball is mu(1+e)cosCv=u√(sin2α+e2cos2α)Dv=tanα - Question 2 - Select One
A glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
A√e2a2+b2 at angle tan−1(aeb) to the verticalB√a2+e2b2 at angle tan−1(aeb) to the verticalC√a2+b2e2 at angle tan−1(eab) to the verticalD√a2e2+b2 at angle tan−1(aeb) to the vertical - Question 3 - Select One
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
A ball P is moving with a certain velocity , collides head-on with another ball Q of same mass is rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionA ball strikes a smooth horizontal floor at an angle α with the normal to the surface and after rebounding from the floor , ball moves at an angle β with the normal . Find the relation between α and β if coefficient of elasticity is e .
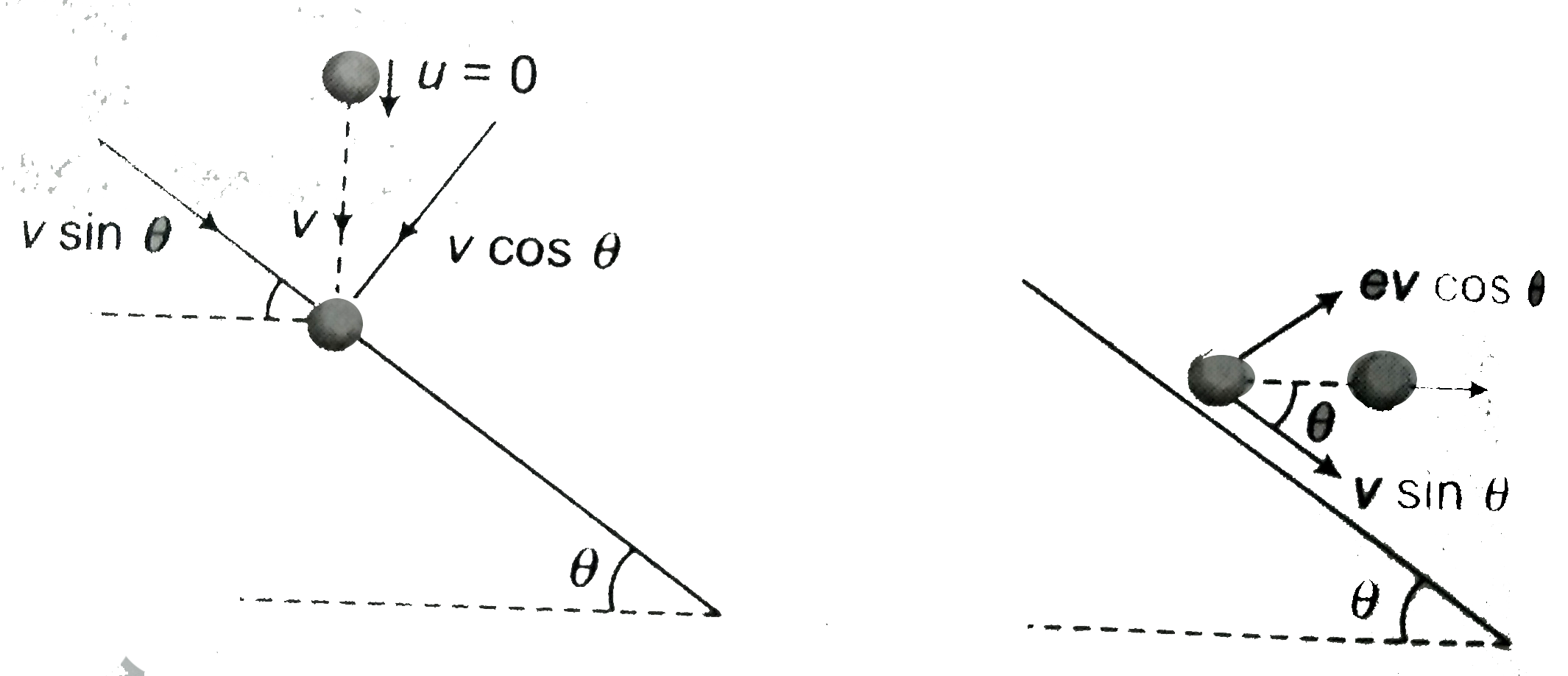
View SolutionA ball after falling a distance collides an inclined plane of inclination θ. If after the collision , the ball moves horizontally , find the coefficient of restitution.
 View Solution
View SolutionA ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
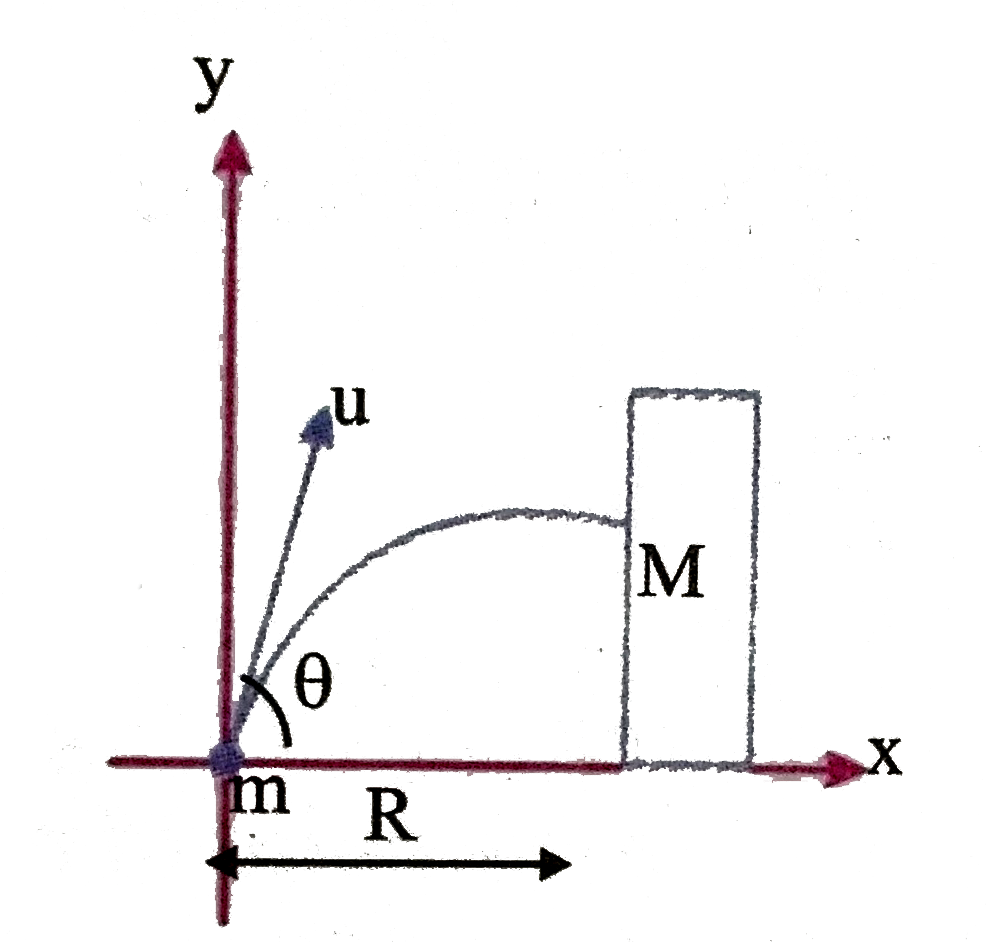
FInd the velocity of the ball after collisionView SolutionA ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?
View Solution

