A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius 0.5m about the hole with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shorting the radius of the circle in which the block revolves. The breaking strength of the cord is 600N. What will be radius of the circle when the cord breaks?

The tension of the rope is the only net force on the block and it does not exert any torque about the axis of rotation. Hence the angular momentum of the block about the axis should remain conserved.
⇒mvr=constant
Let r1=0.5m and v1=4m/s
Let r2,v2,T2 be the radius velocity of and tensio, respectively. when the string breaks
⇒T2=600N
mv1r1=mv2r2= and T2=mv22/r2
⇒mv1r1=m√r2T2mr2
r2=⎛⎜⎝v21r21(T2)13=4×16×0.25600⎞⎟⎠13=(16600)13=3.0m

Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A small block of mass 4 kg is attached to a cord passing through a hole in a horizontal frictionless syurface . The block is originally revolving in a circle of radius 0.5 m about the hole , with a tangential velocity of 4 m/s . The cord is then pulled slowly from below , shortening the radius of the circle in which the block revolves . The breaking strength of the cord is 600 N . What will be the radius of the circle when the cord breaks ?
View SolutionA block of mass 0.1 kg is attached to a cord passing through a hole in a horizontal frictionless horizontal surface as shown in the figure. The block is originally revolving at a distance of 0.4 m from the hole, with an angular velocity of 2 rad s−1. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.2 m. Considering the block to be point mass, calculate the new angular velocity (in rad s−1)
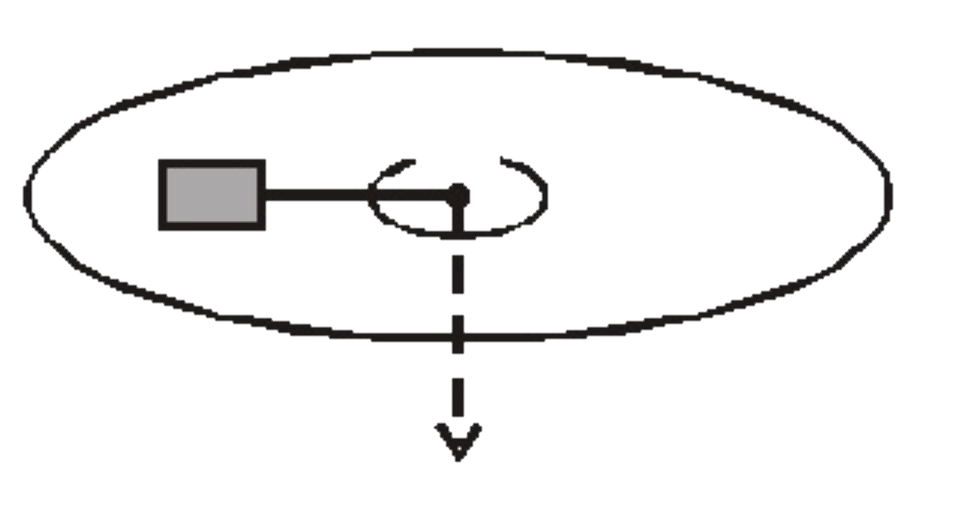
View Solution
Knowledge Check
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
What will be the radius of the circle when the cord breaks?A4.0mB1.0mC3.0mD2.0mA small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
Velocity of the block at the time of breaking of the stringA10m/sB20m/sC7.5m/sD12.5m/sA puck of mass m=50.0g is attached to a taut cord passing through a small hole in a frictionless, horizontal surface (Fig.) The puck is initially orbiting with speed vi=1.50m/s in a circle of radius ri=0.30m. The cord is then slowly pulled from below, decreasing the radius of the circle to r=0.10m. The puck's speed at the smaller radius is.
 .A2.25m/sB5.50m/sC4.50m/sD6.0m/s
.A2.25m/sB5.50m/sC4.50m/sD6.0m/s
A small block of mass m on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius r with speed v and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to r/2. (a) Find the tension in the string when the block moves in a circle of radius r/2. (b) Calculate the change in the kinetic energy of the block.

View SolutionA point mass is tied to one end of a cord whose other end passes through a vertical hollow tube , caught in one hand. The point mass is being rotated in a horizontal circle ofradius 2 m with speed of 4m/sec.The cord is then pulled down so that the radius of the circle reduces to 1m . Compute the new linear and angular velocities of the point mass and compute the kinetic energies under the initial and final states.
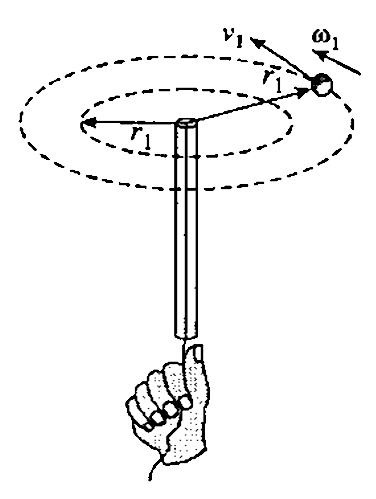
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA small block is rotating in a horizontal circle at the end of a thread which passes down through a hole at the centre of table top. If the system is rotating at 2.5 rps in a circle of 30 cm radius, what will be the speed of rotation when the thread is pulled inwards to decrease the radius to 10 cm ? Neglect friction.
View SolutionA block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?

View Solution
