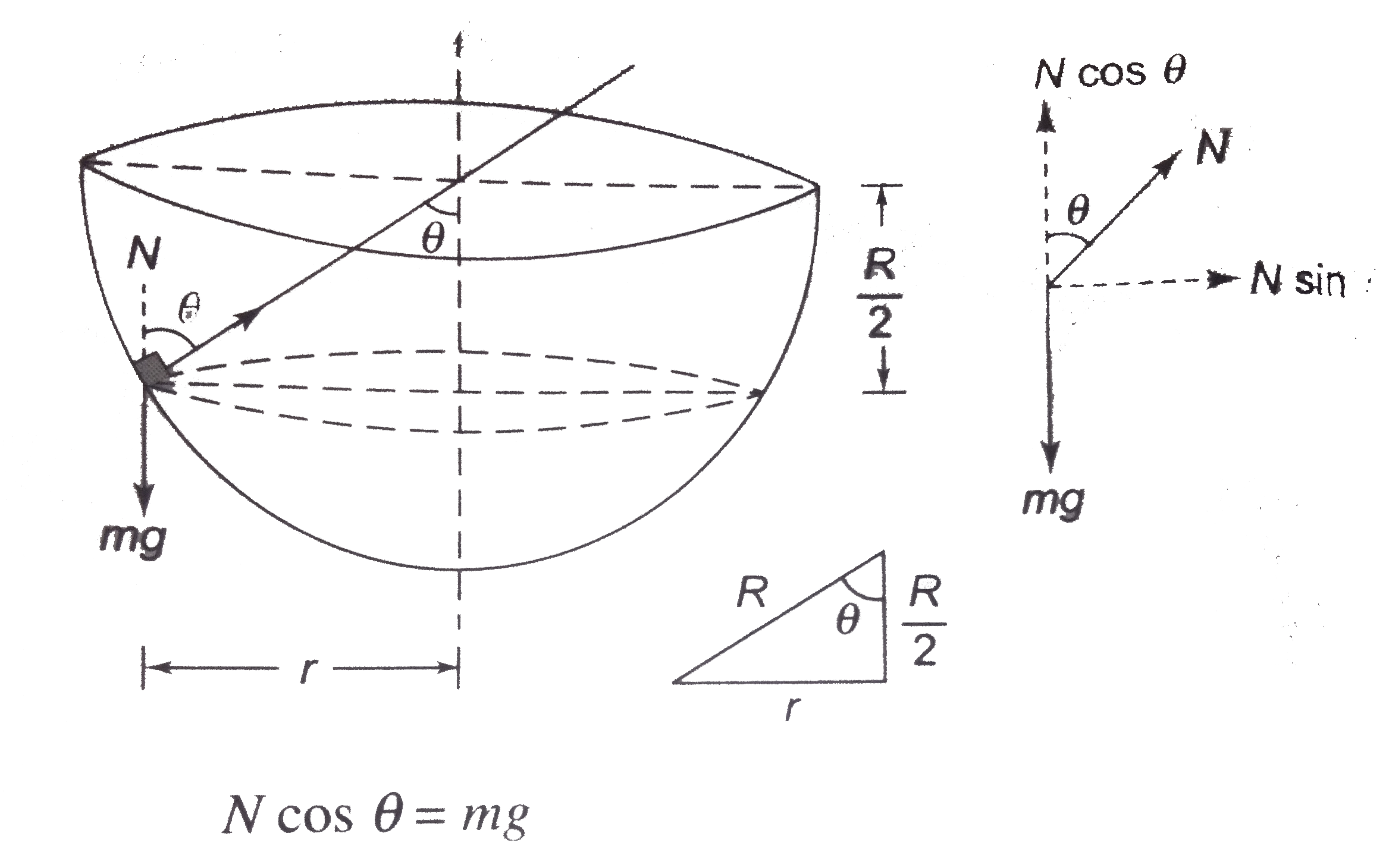
A small block of mass m moving on inside of the smooth hemisphere of radius R, describes a horizontal circle at a distance R/2 below the centre of the sphere. Find the time period of revolution and force with which the block pushes against the hemisphere.
Ncosθ=mg ….(i)
⇒N=mgcosθ=mg1/2=2mg
Nsinθθ=mω2r …..(ii)
Nsinθ=mω2Rsinθ
⇒N=mω2Rsinθ
⇒N=mω2R
2mg=mω2R
⇒ω2=2gR⇒ω=√2gR
Time period T0=2πω=2π√R2g
Topper's Solved these Questions
Similar Questions
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?
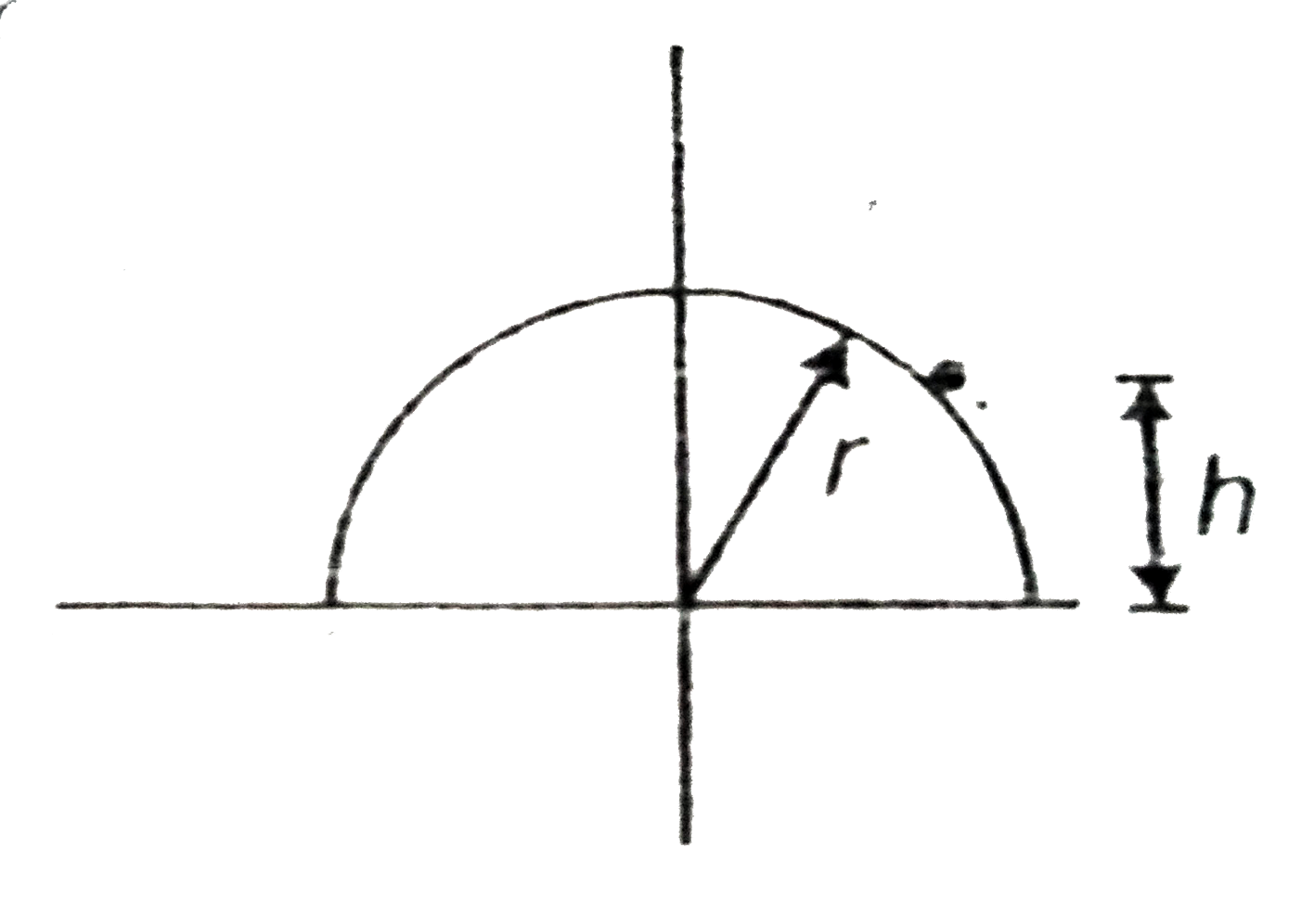
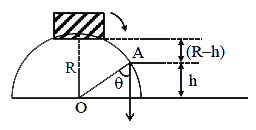
View SolutionA small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
View Solution
Knowledge Check
A particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
A√5grB√4gr/3C√3gr/2D√√3grA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
AR4BR3CR2DRA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
A smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution
